Control de robots móviles con ruedas

MT3005 - Robótica 1

Partiendo del robot diferencial

{^I}\dot{\boldsymbol{\xi}}=\dfrac{r}{2}\begin{bmatrix} \cos\theta & \cos\theta \\ \sin\theta & \sin\theta \\ 1/\ell & -1/\ell \end{bmatrix} \begin{bmatrix} \dot{\varphi}_R \\ \dot{\varphi}_L \end{bmatrix}

\ell

v_r

v_\ell

\dot{x}=\dfrac{r\left(\dot{\varphi}_R+\dot{\varphi}_L\right)}{2}\cos\theta

\dot{y}=\dfrac{r\left(\dot{\varphi}_R+\dot{\varphi}_L\right)}{2}\sin\theta

\dot{\theta}=\dfrac{r\left(\dot{\varphi}_R-\dot{\varphi}_L\right)}{2\ell}

\ell

v_r

v_\ell

\dot{x}=\dfrac{r\left(\dot{\varphi}_R+\dot{\varphi}_L\right)}{2}\cos\theta

\dot{y}=\dfrac{r\left(\dot{\varphi}_R+\dot{\varphi}_L\right)}{2}\sin\theta

\dot{\theta}=\dfrac{r\left(\dot{\varphi}_R-\dot{\varphi}_L\right)}{2\ell}

ya con el modelo del robot procedamos a controlarlo

sistema dinámico simple pero que presenta un comportamiento representativo del sistema completo

modelo de orden reducido (template)

Otra arquitectura jerárquica de control

sistema completo con actuadores ideales

referencias

sistema dinámico simple pero que presenta un comportamiento representativo del sistema completo

sistema dinámico como convencionalmente lo conocemos

modelo de orden reducido (template)

Otra arquitectura jerárquica de control

sistema completo con actuadores ideales

actuadores reales

referencias

servomecanismos a bajo nivel

sistema dinámico simple pero que presenta un comportamiento representativo del sistema completo

sistema dinámico como convencionalmente lo conocemos

modelo de orden reducido (template)

Otra arquitectura jerárquica de control

sistema completo con actuadores ideales

actuadores reales

referencias

servomecanismos a bajo nivel

(control clásico)

sistema dinámico simple pero que presenta un comportamiento representativo del sistema completo

(control moderno | IA )

sistema dinámico como convencionalmente lo conocemos

(control moderno)

modelo de orden reducido (template)

Otra arquitectura jerárquica de control

sistema completo con actuadores ideales

actuadores reales

referencias

servomecanismos a bajo nivel

(control clásico)

sistema dinámico simple pero que presenta un comportamiento representativo del sistema completo

(control moderno | IA )

sistema dinámico como convencionalmente lo conocemos

(control moderno)

modelo de orden reducido (template)

¿Por qué no emplear control convencional?

el comportamiento no holonómico de la mayoría de robots móviles con ruedas genera dificultades para el control

por ejemplo, ¿Qué pasa si tratamos de aplicar control LTI directamente?

el comportamiento no holonómico de la mayoría de robots móviles con ruedas genera dificultades para el control

por ejemplo, ¿Qué pasa si tratamos de aplicar control LTI directamente?

\mathbf{f}\left({^I}\boldsymbol{\xi}_{ss},\mathbf{v}_{ss}\right)=\mathbf{0}

el comportamiento no holonómico de la mayoría de robots móviles con ruedas genera dificultades para el control

por ejemplo, ¿Qué pasa si tratamos de aplicar control LTI directamente?

\mathbf{f}\left({^I}\boldsymbol{\xi}_{ss},\mathbf{v}_{ss}\right)=\mathbf{0}

{^I}\boldsymbol{\xi}_{ss}=\begin{bmatrix} x_{ss} & y_{ss} & \theta_{ss} \end{bmatrix}^\top \\ \mathbf{v}_{ss}=\mathbf{0}

\begin{cases} \dot{\mathbf{z}}=\mathbf{A}\mathbf{z}+\mathbf{B}\boldsymbol{\mu} \\ \mathbf{w}=\mathbf{C}\mathbf{z} \end{cases}

{^I}\boldsymbol{\xi}_{ss}=\begin{bmatrix} x_{ss} & y_{ss} & \theta_{ss} \end{bmatrix}^\top \\ \mathbf{v}_{ss}=\mathbf{0}

\begin{cases} \dot{\mathbf{z}}=\mathbf{A}\mathbf{z}+\mathbf{B}\boldsymbol{\mu} \\ \mathbf{w}=\mathbf{C}\mathbf{z} \end{cases}

{^I}\boldsymbol{\xi}_{ss}=\begin{bmatrix} x_{ss} & y_{ss} & \theta_{ss} \end{bmatrix}^\top \\ \mathbf{v}_{ss}=\mathbf{0}

¿Problema?

el sistema linealizado nunca resulta completamente controlable

\begin{cases} \dot{\mathbf{z}}=\mathbf{A}\mathbf{z}+\mathbf{B}\boldsymbol{\mu} \\ \mathbf{w}=\mathbf{C}\mathbf{z} \end{cases}

{^I}\boldsymbol{\xi}_{ss}=\begin{bmatrix} x_{ss} & y_{ss} & \theta_{ss} \end{bmatrix}^\top \\ \mathbf{v}_{ss}=\mathbf{0}

¿Problema?

el sistema linealizado nunca resulta completamente controlable

\(\Rightarrow\) no pueden emplearse de forma directa los métodos convencionales

modelo uniciclo*

(o boid)

modelo cinemático del robot móvil

motores con ruedas

controlados mediante PIDs (típicamente) de velocidad

el modelo más simple que representa el comportamiento no holonómico de los robots con ruedas (y otros)

derivado con la metodología de la clase anterior

v_\mathrm{ref}, \omega_\mathrm{ref}

\dot{\varphi}_{R,\mathrm{ref}}, \dot{\varphi}_{L,\mathrm{ref}}

Regresando a la arquitectura jerárquica

(x,y)

\theta

El modelo uniciclo

(x,y)

\theta

\omega

El modelo uniciclo

\dot{x}=v\cos\theta \\ \dot{y}=v\sin\theta \\ \dot{\theta}=\omega

(x,y)

\theta

\omega

El modelo uniciclo

\begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{bmatrix} = \begin{bmatrix} \cos\theta & 0 \\ \sin\theta & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} v \\ \omega \end{bmatrix}

(x,y)

\theta

\omega

El modelo uniciclo

\begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{bmatrix} = \begin{bmatrix} \cos\theta & 0 \\ \sin\theta & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} v \\ \omega \end{bmatrix}

(x,y)

\theta

\omega

El modelo uniciclo

\mathbf{J}\left({^I}\boldsymbol{\xi}\right)

{^I}\dot{\boldsymbol{\xi}}

\mathbf{v}

\begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{bmatrix} = \begin{bmatrix} \cos\theta & 0 \\ \sin\theta & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} v \\ \omega \end{bmatrix}

(x,y)

\theta

\omega

El modelo uniciclo

\mathbf{v}

este modelo aplica para cualquier sistema capaz de moverse hacia adelante y cambiar su dirección

\mathbf{J}\left({^I}\boldsymbol{\xi}\right)

{^I}\dot{\boldsymbol{\xi}}

El modelo uniciclo

control clásico (posición)
- PID
- PID con acercamiento exponencial
control moderno LTI (posición)
- LQR
- LQI
control no lineal (pose)

Controlando al uniciclo

Directamente, mediante el sistema no holonómico (no lineal):

PID planteado de forma "ingenua" (punto a punto).
- Modificación de velocidad lineal con acercamiento exponencial.
- Trayectorias mediante pure pursuit y con términos de feedforward.
Planteamientos basados en Lyapunov.

Controlando al uniciclo

Indirectamente, mediante linealización por difeomorfismo:

PIDs desacoplados (ej: control BART - Tarea IE3036).
LQR (punto a punto) y LQI (trayectorias).
Entre otras metodologías de control lineal.

Controlando al uniciclo

Indirectamente, mediante linealización por difeomorfismo:

PIDs desacoplados (ej: control BART - Tarea IE3036).
LQR (punto a punto) y LQI (trayectorias).
Entre otras metodologías de control lineal.

NOTA: las opciones presentadas NO son exhaustivas ya que ni siquiera estamos considerando las estrategias de control típicas en el área de vehículos autónomos.

(x,y)

\theta

(x_g,y_g)

PID de forma ingenua

(x,y)

\theta

(x_g,y_g)

PID de forma ingenua

\theta_g=\arctan\left(\dfrac{y_g-y}{x_g-x}\right)

(x,y)

\theta

(x_g,y_g)

x_g-x

y_g-y

\theta_g

PID de forma ingenua

e_p=\left\| \begin{bmatrix} x_g-x \\ y_g-y \end{bmatrix} \right\|_2

\theta_g=\arctan\left(\dfrac{y_g-y}{x_g-x}\right)

(x,y)

\theta

(x_g,y_g)

x_g-x

y_g-y

\theta_g

e_p

PID de forma ingenua

e_p=\left\| \begin{bmatrix} x_g-x \\ y_g-y \end{bmatrix} \right\|_2

\theta_g=\arctan\left(\dfrac{y_g-y}{x_g-x}\right)

(x,y)

\theta

(x_g,y_g)

x_g-x

y_g-y

\theta_g

e_o

e_p

e_o=\theta_g-\theta

PID de forma ingenua

e_p=\left\| \begin{bmatrix} x_g-x \\ y_g-y \end{bmatrix} \right\|_2

\theta_g=\arctan\left(\dfrac{y_g-y}{x_g-x}\right)

(x,y)

\theta

(x_g,y_g)

x_g-x

y_g-y

\theta_g

e_o

e_p

e_o=\theta_g-\theta

PID de forma ingenua

PROBLEMA

e_p=\left\| \begin{bmatrix} x_g-x \\ y_g-y \end{bmatrix} \right\|_2

\theta_g=\arctan\left(\dfrac{y_g-y}{x_g-x}\right)

(x,y)

\theta

(x_g,y_g)

x_g-x

y_g-y

\theta_g

e_o

e_p

PID de forma ingenua

e_o=\mathrm{atan2}\left(\dfrac{\sin(\theta_g-\theta)}{\cos(\theta_g-\theta)}\right)

e_p=\left\| \begin{bmatrix} x_g-x \\ y_g-y \end{bmatrix} \right\|_2

\theta_g=\arctan\left(\dfrac{y_g-y}{x_g-x}\right)

(x,y)

\theta

(x_g,y_g)

x_g-x

y_g-y

\theta_g

e_o

e_p

PID de forma ingenua

eO = angdiff(theta, theta_g)

v = \mathrm{PID}(e_p)=k_{Pp}e_p + k_{Ip}\displaystyle\int_{0}^{t} e_p(\tau)d\tau + k_{Dp}\dot{e}_p \\ \omega = \mathrm{PID}(e_o)=k_{Po}e_o + k_{Io}\displaystyle\int_{0}^{t} e_o(\tau)d\tau + k_{Do}\dot{e}_o

PIDs de posición y orientación

este esquema desacopla la posición de la orientación y las controla por separado

\(\Rightarrow\) la convergencia se da en forma de espirales

PIDs de posición y orientación

un problema que presenta el PID para la velocidad lineal es que el robot desacelera exponencialmente conforme se acerca a la meta, presentando una convergencia lenta

Acercamiento exponencial

un problema que presenta el PID para la velocidad lineal es que el robot desacelera exponencialmente conforme se acerca a la meta, presentando una convergencia lenta

Acercamiento exponencial

esto puede corregirse (hasta cierto punto) mediante una no linealidad que normalice la velocidad lineal, para que el robot frene hasta estar cercano a la meta

v = k(e_p)e_p=\dfrac{v_0\left(1-e^{-\alpha e_p^2}\right)}{e_p}e_p

Acercamiento exponencial

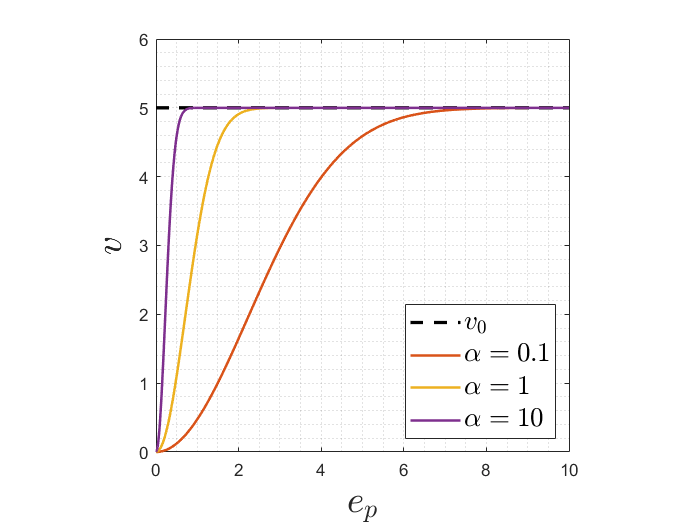
v = k(e_p)e_p=\dfrac{v_0\left(1-e^{-\alpha e_p^2}\right)}{e_p}e_p

Acercamiento exponencial

coeficiente de ajuste

velocidad lineal nominal o máxima

v = k(e_p)e_p=\dfrac{v_0\left(1-e^{-\alpha e_p^2}\right)}{e_p}e_p

Acercamiento exponencial

>> mt3005_clase13_unicycle_pid.m

¿Trayectorias?

el controlador PID permite que el uniciclo ejecute trayectorias simplemente al cambiar el punto meta en el tiempo, es decir

¿Trayectorias?

el controlador PID permite que el uniciclo ejecute trayectorias simplemente al cambiar el punto meta en el tiempo, es decir

(x_g,y_g) \to \left(x_g(t),y_g(t)\right)

¿Trayectorias?

donde las metas cambiantes son puntos individuales de la trayectoria generada

el controlador PID permite que el uniciclo ejecute trayectorias simplemente al cambiar el punto meta en el tiempo, es decir

(x_g,y_g) \to \left(x_g(t),y_g(t)\right)

Pure pursuit

esta estrategia recibe el nombre de pure pursuit ya que se hala el punto meta para seguir empleando un control punto a punto, en lugar de usar un controlador de trayectoria

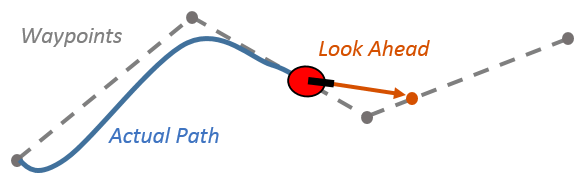
Pure pursuit

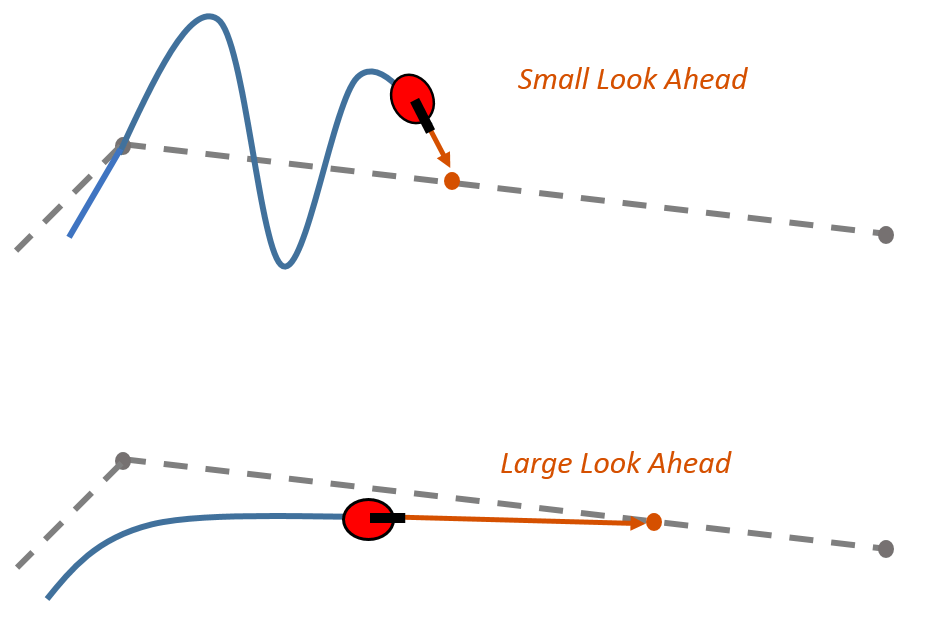
Look Ahead \(\equiv\) capacidad "predictiva"

Pure pursuit

>> mt3005_clase13_unicycle_pid.m

Términos feedforward

otra forma de dotar con capacidad predictiva al controlador PID (y el resto) es mediante términos feedforward de velocidad de control

\mathbf{v}_{ss}(t)=\mathbf{J}^\dagger\left(\boldsymbol{\xi}\right) \dot{\boldsymbol{\xi}}_d(t)

Términos feedforward

estos emplean el modelo junto con la velocidad de la trayectoria para pre-calcular la velocidad requerida por el robot en open-loop

otra forma de dotar con capacidad predictiva al controlador PID (y el resto) es mediante términos feedforward de velocidad de control

\mathbf{v}_{ss}(t)=\mathbf{J}^\dagger\left(\boldsymbol{\xi}\right) \dot{\boldsymbol{\xi}}_d(t)

Términos feedforward

feedback

(robustez)

recordemos la efectividad de la mezcla

\mathbf{v}_\mathrm{ctrl}=\mathbf{v}\left(e_p,e_o\right) \quad + \quad \mathbf{v}_{ss}(t)

feedforward

(rapidez)

\mathbf{v}\left(e_p,e_o\right)

\mathbf{v}_{ss}(t)

para "arreglar" la falta de controlabilidad puede emplearse el siguiente "truco"

(x,y)

\theta

Linealización por difeomorfismo

para "arreglar" la falta de controlabilidad puede emplearse el siguiente "truco"

(x,y)

\theta

\ell_0

\left(\tilde{x}, \tilde{y}\right)

se define un nuevo punto cercano a la posición del uniciclo

\ell_0 \approx 0

Linealización por difeomorfismo

para "arreglar" la falta de controlabilidad puede emplearse el siguiente "truco"

(x,y)

\theta

\ell_0

\left(\tilde{x}, \tilde{y}\right)

Linealización por difeomorfismo

idea: aproximar al uniciclo con este punto

se define un nuevo punto cercano a la posición del uniciclo

\ell_0 \approx 0

para "arreglar" la falta de controlabilidad puede emplearse el siguiente "truco"

(x,y)

\theta

\ell_0

\left(\tilde{x}, \tilde{y}\right)

Linealización por difeomorfismo

idea: aproximar al uniciclo con este punto

se define un nuevo punto cercano a la posición del uniciclo

\ell_0 \approx 0

\(\Rightarrow\) necesitamos su dinámica

\tilde{x}=x+\ell_0\cos\theta \\ \tilde{y}=y+\ell_0\sin\theta

\dot{\tilde{x}}=\dot{x}-\ell_0\sin\theta\dot{\theta} \\ \dot{\tilde{y}}=\dot{y}+\ell_0\cos\theta\dot{\theta}

supondremos que podemos controlar | actuar directamente al punto \((\tilde{x},\tilde{y})\)

u_1

u_2

=u_1 \\ =u_2

\tilde{x}=x+\ell_0\cos\theta \\ \tilde{y}=y+\ell_0\sin\theta

\dot{\tilde{x}}=\dot{x}-\ell_0\sin\theta\dot{\theta} \\ \dot{\tilde{y}}=\dot{y}+\ell_0\cos\theta\dot{\theta}

supondremos que podemos controlar | actuar directamente al punto \((\tilde{x},\tilde{y})\)

\begin{bmatrix} \dot{\tilde{x}} \\ \dot{\tilde{y}} \end{bmatrix}= \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & \ell_0 \end{bmatrix} \begin{bmatrix} v \\ \omega \end{bmatrix} =\begin{bmatrix} u_1 \\ u_2 \end{bmatrix}

u_1

u_2

=u_1 \\ =u_2

\tilde{x}=x+\ell_0\cos\theta \\ \tilde{y}=y+\ell_0\sin\theta

\dot{\tilde{x}}=\dot{x}-\ell_0\sin\theta\dot{\theta} \\ \dot{\tilde{y}}=\dot{y}+\ell_0\cos\theta\dot{\theta}

matriz diagonal de ajuste

{^I}\mathbf{R}_B(\theta)

\begin{bmatrix} v \\ \omega \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0 & 1/\ell_0 \end{bmatrix} {^I}\mathbf{R}_B^{-1}(\theta) \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}

matriz diagonal de ajuste

{^I}\mathbf{R}_B(\theta)

\mathbf{v}= \mathbf{M}(\ell_0,\theta) \mathbf{u}

difeomorfismo que mapea las velocidades virtuales a las del uniciclo

\mathbf{M}(\ell_0,\theta)

\begin{bmatrix} v \\ \omega \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0 & 1/\ell_0 \end{bmatrix} {^I}\mathbf{R}_B^{-1}(\theta) \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}

matriz diagonal de ajuste

{^I}\mathbf{R}_B(\theta)

\begin{bmatrix} \dot{\tilde{x}} \\ \dot{\tilde{y}} \end{bmatrix}= \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} \equiv \begin{bmatrix} \dot{\tilde{x}} \\ \dot{\tilde{y}} \end{bmatrix}= \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} \tilde{x} \\ \tilde{y} \end{bmatrix}+ \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} u_1 \\ u_2 \end{bmatrix}

por lo tanto

Estabilización por LQR

por lo tanto

\dot{\mathbf{x}}

\mathbf{A}

\mathbf{x}

\mathbf{B}

\mathbf{u}

Estabilización por LQR

por lo tanto

\dot{\mathbf{x}}

\mathbf{A}

\mathbf{x}

\mathbf{B}

\mathbf{u}

\mathbf{x}_{ss}=\begin{bmatrix} x_g \\ y_g \end{bmatrix}

\mathbf{Q}=\mathbf{R}=\mathbf{I}_2

\mathbf{v}= \mathbf{M}(\ell_0,\theta) \mathbf{u}

Estabilización por LQR

por lo tanto

\dot{\mathbf{x}}

\mathbf{A}

\mathbf{x}

\mathbf{B}

\mathbf{u}

\mathbf{v}= \mathbf{M}(\ell_0,\theta) \mathbf{u}

Rastreo por LQI

\mathbf{r}=\begin{bmatrix} x_g \\ y_g \end{bmatrix}

\boldsymbol{\mathcal{Q}}=\mathbf{I}_4

\boldsymbol{\mathcal{R}}=\mathbf{I}_2

\mathbf{y}_r=\begin{bmatrix} x \\ y \end{bmatrix}

por lo tanto

\dot{\mathbf{x}}

\mathbf{A}

\mathbf{x}

\mathbf{B}

\mathbf{u}

Rastreo por LQI

\mathbf{v}= \mathbf{M}(\ell_0,\theta) \mathbf{u}

\mathbf{r}=\begin{bmatrix} x_g \\ y_g \end{bmatrix}

\boldsymbol{\mathcal{Q}}=\mathbf{I}_4

\boldsymbol{\mathcal{R}}=\mathbf{I}_2

\mathbf{y}_r=\begin{bmatrix} x \\ y \end{bmatrix}

>> mt3005_clase13_unicycle_lqrlqi.m

Regresando al robot

para el caso particular del robot diferencial podemos notar que

\dot{x}=\dfrac{r\left(\dot{\varphi}_R+\dot{\varphi}_L\right)}{2}\cos\theta

\dot{y}=\dfrac{r\left(\dot{\varphi}_R+\dot{\varphi}_L\right)}{2}\sin\theta

\dot{\theta}=\dfrac{r\left(\dot{\varphi}_R-\dot{\varphi}_L\right)}{2\ell}

\ell

v_r

v_\ell

Del uniciclo de regreso al robot móvil

para el caso particular del robot diferencial podemos notar que

\dot{x}=\dfrac{r\left(\dot{\varphi}_R+\dot{\varphi}_L\right)}{2}\cos\theta

\dot{y}=\dfrac{r\left(\dot{\varphi}_R+\dot{\varphi}_L\right)}{2}\sin\theta

\dot{\theta}=\dfrac{r\left(\dot{\varphi}_R-\dot{\varphi}_L\right)}{2\ell}

\ell

v_r

v_\ell

\(v\) del uniciclo

\(\omega\) del uniciclo

Del uniciclo de regreso al robot móvil

v=\dfrac{r\left(\dot{\varphi}_R+\dot{\varphi}_L\right)}{2}

\omega=\dfrac{r\left(\dot{\varphi}_R-\dot{\varphi}_L\right)}{2\ell}

Del uniciclo de regreso al robot móvil

para el caso particular del robot diferencial podemos notar que

v=\dfrac{r\left(\dot{\varphi}_R+\dot{\varphi}_L\right)}{2}

\omega=\dfrac{r\left(\dot{\varphi}_R-\dot{\varphi}_L\right)}{2\ell}

y entonces

\dot{\varphi}_{R,\mathrm{ctrl}}=\dfrac{v_\mathrm{ctrl}+\ell\omega_\mathrm{ctrl}}{r} \qquad \dot{\varphi}_{L,\mathrm{ctrl}}=\dfrac{v_\mathrm{ctrl}-\ell\omega_\mathrm{ctrl}}{r}

Del uniciclo de regreso al robot móvil

para el caso particular del robot diferencial podemos notar que

La metodología para controlar robots móviles no holonómicos se resume entonces como:

se muestra que el modelo del robot puede mapearse al uniciclo.
se controla al uniciclo, para encontrar las velocidades de control \(v_\mathrm{ctrl}\) y \(\omega_\mathrm{ctrl}\).
se mapean las velocidades de control de regreso al robot real.

Del uniciclo de regreso al robot móvil

La metodología para controlar robots móviles no holonómicos se resume entonces como:

se muestra que el modelo del robot puede mapearse al uniciclo.
se controla al uniciclo, para encontrar las velocidades de control \(v_\mathrm{ctrl}\) y \(\omega_\mathrm{ctrl}\).
se mapean las velocidades de control de regreso al robot real.

Del uniciclo de regreso al robot móvil

Laboratorio 11

Addendum

Otros controladores para el uniciclo

Control no lineal de pose

(x,y)

\theta

(x_g,y_g)

x_B

y_B

\{G\}

x_G

y_G

\beta

\Delta x

\Delta y

\| \cdot \|_2=\rho

\{B\}

\alpha

Control no lineal de pose

x_B

y_B

\{G\}

x_G

y_G

\beta

\{B\}

Control no lineal de pose

(x,y)

\theta

(x_g,y_g)

x_B

y_B

\{G\}

x_G

y_G

\beta

\Delta x

\Delta y

\{B\}

Control no lineal de pose

(x,y)

\theta

(x_g,y_g)

x_B

y_B

\{G\}

x_G

y_G

\beta

\Delta x

\Delta y

\| \cdot \|_2=\rho

\{B\}

\alpha

Control no lineal de pose

(x,y)

\theta

(x_g,y_g)

x_B

y_B

\{G\}

x_G

y_G

\beta

\Delta x

\Delta y

\| \cdot \|_2=\rho

\{B\}

\alpha

se realiza el cambio de coordenadas

\rho=\sqrt{\Delta x^2 +\Delta y^2} \\ \alpha=-\theta+\mathrm{atan2}\left(\Delta y, \Delta x\right) \\ \beta=-\theta-\alpha

Control no lineal de pose

(x,y)

\theta

(x_g,y_g)

x_B

y_B

\{G\}

x_G

y_G

\beta

\Delta x

\Delta y

\| \cdot \|_2=\rho

\{B\}

\alpha

se realiza el cambio de coordenadas

\rho=\sqrt{\Delta x^2 +\Delta y^2} \\ \alpha=-\theta+\mathrm{atan2}\left(\Delta y, \Delta x\right) \\ \beta=-\theta-\alpha

OJO: esto corresponde a un mejor planteamiento del controlador PID

Control no lineal de pose

(x,y)

\theta

(x_g,y_g)

x_B

y_B

\{G\}

x_G

y_G

\beta

\Delta x

\Delta y

\| \cdot \|_2=\rho

\{B\}

\alpha

se realiza el cambio de coordenadas

\rho=\sqrt{\Delta x^2 +\Delta y^2} \\ \alpha=-\theta+\mathrm{atan2}\left(\Delta y, \Delta x\right) \\ \beta=-\theta-\alpha

puede igualmente hacerse el ajuste con

angdiff

Control no lineal de pose

(x,y)

\theta

(x_g,y_g)

x_B

y_B

\{G\}

x_G

y_G

\beta

\Delta x

\Delta y

\| \cdot \|_2=\rho

\{B\}

\alpha

se realiza el cambio de coordenadas

\rho=\sqrt{\Delta x^2 +\Delta y^2} \\ \alpha=-\theta+\mathrm{atan2}\left(\Delta y, \Delta x\right) \\ \beta=-\theta-\alpha

puede igualmente hacerse el ajuste con

angdiff

puede hacerse el ajuste de acercamiento exponencial

si se restringe a \(\alpha \in \left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right) \) podemos hacer un cambio de coordenadas y obtener el nuevo sistema dinámico

\begin{bmatrix} \dot{\rho} \\ \dot{\alpha} \\ \dot{\beta} \end{bmatrix}= \begin{bmatrix} -\cos\alpha & 0 \\ \sin\alpha/\rho & -1 \\ -\sin\alpha/\rho & 0 \end{bmatrix} \begin{bmatrix} v \\ \omega \end{bmatrix}

si se restringe a \(\alpha \in \left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right) \) podemos hacer un cambio de coordenadas y obtener el nuevo sistema dinámico

hace que el robot se mueva hacia adelante

si se restringe a \(\alpha \in \left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right) \) podemos hacer un cambio de coordenadas y obtener el nuevo sistema dinámico

hace que el robot se mueva hacia adelante

puede redefinirse \(v=-v\)

\Rightarrow \begin{bmatrix} \dot{\rho} \\ \dot{\alpha} \\ \dot{\beta} \end{bmatrix}= \begin{bmatrix} \cos\alpha & 0 \\ -\sin\alpha/\rho & 1 \\ \sin\alpha/\rho & 0 \end{bmatrix} \begin{bmatrix} v \\ \omega \end{bmatrix}

en este nuevo sistema de coordenadas, el controlador

v=k_\rho \rho \\ \omega=k_\alpha \alpha + k_\beta \beta

k_\rho>0, \quad k_\beta < 0 \\ k_\alpha+\frac{5}{3}k_\beta-\frac{2}{\pi}k_\rho>0

en este nuevo sistema de coordenadas, el controlador

v=k_\rho \rho \\ \omega=k_\alpha \alpha + k_\beta \beta

k_\rho>0, \quad k_\beta < 0 \\ k_\alpha+\frac{5}{3}k_\beta-\frac{2}{\pi}k_\rho>0

garantiza que el punto \((\rho,\alpha,\beta)=(0,0,0)\) sea globalmente asintóticamente estable...

en este nuevo sistema de coordenadas, el controlador

v=k_\rho \rho \\ \omega=k_\alpha \alpha + k_\beta \beta

k_\rho>0, \quad k_\beta < 0 \\ k_\alpha+\frac{5}{3}k_\beta-\frac{2}{\pi}k_\rho>0

garantiza que el punto \((\rho,\alpha,\beta)=(0,0,0)\) sea globalmente asintóticamente estable...

... y que no cambie de dirección de movimiento al acercarse a la meta

en este nuevo sistema de coordenadas, el controlador

v=k_\rho \rho \\ \omega=k_\alpha \alpha + k_\beta \beta

k_\rho>0, \quad k_\beta < 0 \\ k_\alpha+\frac{5}{3}k_\beta-\frac{2}{\pi}k_\rho>0

garantiza que el punto \((\rho,\alpha,\beta)=(0,0,0)\) sea globalmente asintóticamente estable...

>> mt3005_clase13_unicycle_nonlin.m

en este nuevo sistema de coordenadas, el controlador

v=k_\rho \rho \\ \omega=k_\alpha \alpha + k_\beta \beta

k_\rho>0, \quad k_\beta < 0 \\ k_\alpha+\frac{5}{3}k_\beta-\frac{2}{\pi}k_\rho>0

garantiza que el punto \((\rho,\alpha,\beta)=(0,0,0)\) sea globalmente asintóticamente estable...

NOTA: este controlador siempre "parquea" al robot con su eje \(x\) alineado con el del marco \(\{G\}\).

k_\rho>0, \quad k_\beta < 0 \\ k_\alpha+\frac{5}{3}k_\beta-\frac{2}{\pi}k_\rho>0

en este nuevo sistema de coordenadas, el controlador

v=k_\rho \rho \\ \omega=k_\alpha \alpha + k_\beta \beta

garantiza que el punto \((\rho,\alpha,\beta)=(0,0,0)\) sea globalmente asintóticamente estable...

NOTA: este controlador siempre "parquea" al robot con su eje \(x\) alineado con el del marco \(\{G\}\).

OJO: existen muchos más controladores para el uniciclo, sin embargo los anteriores muestrean un poco de todo lo que hemos visto en los cursos de Sistemas de Control

MT3005 - Lecture 13 (2025)

By Miguel Enrique Zea Arenales

MT3005 - Lecture 13 (2025)

MT3005 - Lecture 13 (2025)

More from Miguel Enrique Zea Arenales