
IE3036 - Sistemas de Control 1
2do ciclo, 2024
Lección 7: Retroalimentación negativa y control proporcional
¿Por qué?
Sistema de control canónico
Nos hemos enfocado en el modelado y análisis de la planta
Objetivo principal del sistema de control: forzar que la planta se comporte de una manera deseada.
¿Qué hace el controlador? ¿Qué es el control en sí?
Antes de contestar eso, estudiemos el fenómeno de retroalimentación negativa.
Retroalimentación negativa
referencia
planta
sensor
controlador
salida
retroalimentación negativa
referencia
salida
retroalimentación negativa
planta
sensor ideal
¿Por qué retroalimentación negativa?
Veamos algunos ejemplos...
Modelo ideal del amplificador operacional.
El modelo más inestable en circuitos electrónicos.
Estabilidad
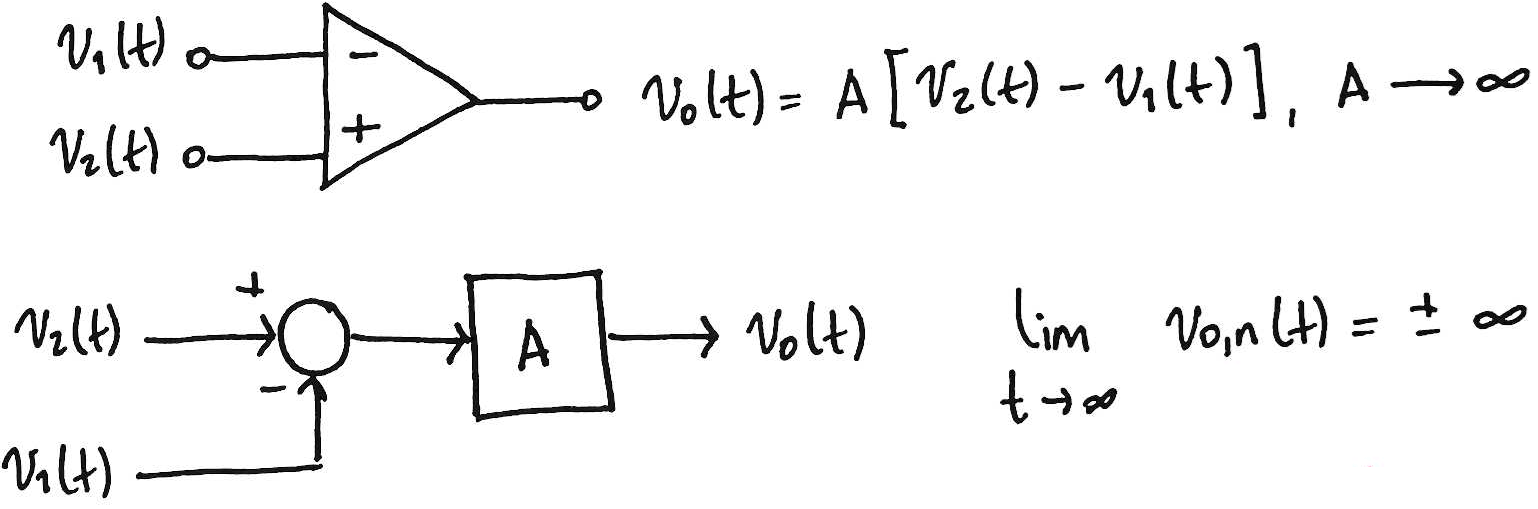
Lazo abierto
Respuesta natural
¿Qué pasa si cerramos el lazo?
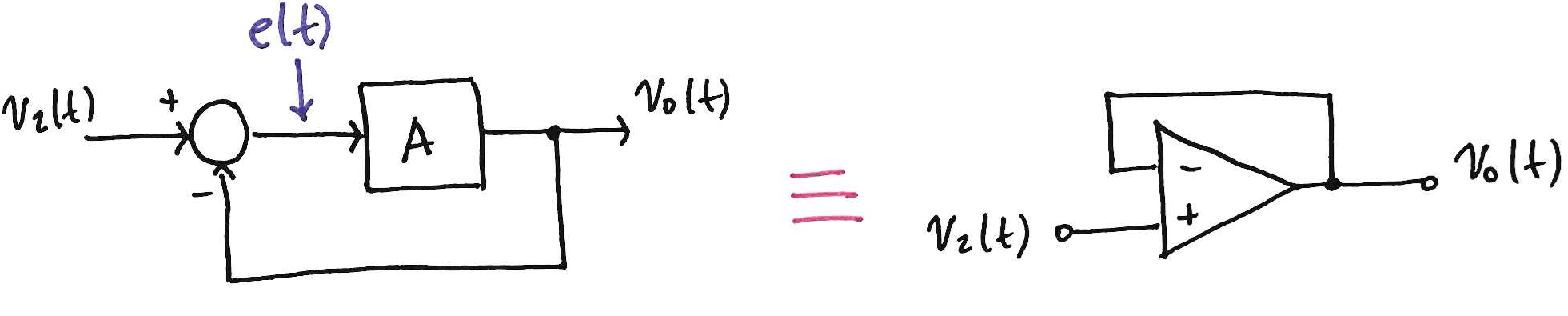
Seguidor de voltaje
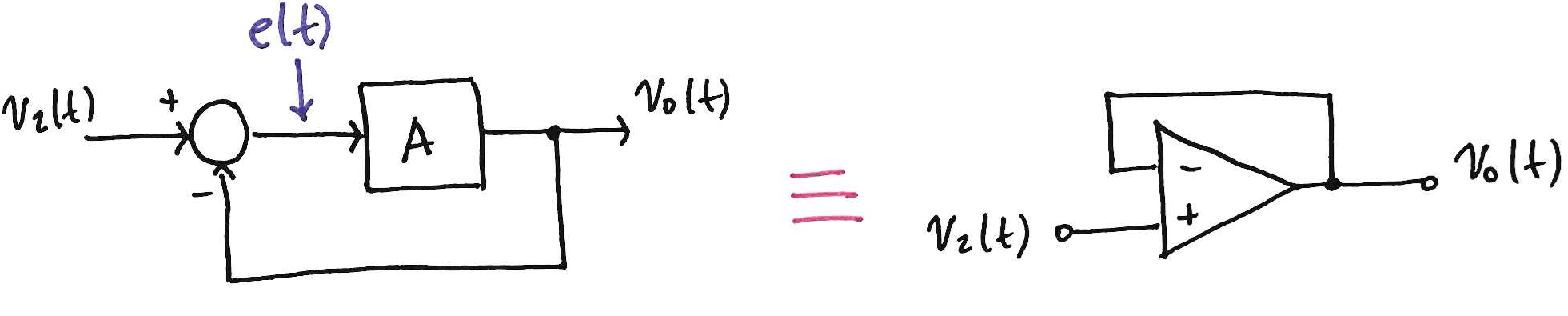
¿Qué pasa si cerramos el lazo?
Seguidor de voltaje
Otra forma de analizar la situación:
veamos el error en estado estacionario, \(e_{ss}\), con \(V_2(t)=\textbf{1}(t)\).
Como \(A\rightarrow \infty\),
Conclusión: la retroalimentación negativa fue capaz de estabilizar un sistema que originalmente era inestable.
Modelo de un motor AC lento.
Rendimiento
Modelo de un motor AC lento.
reducción del 50% del valor original
Sensibilidad a errores de modelado
¿Valor final con entrada de escalón unitario?
open loop
¿Valor final al cerrar el lazo?
closed loop
¿Ventaja? Veamos cuál valor final es más sensible.
siempre es 1
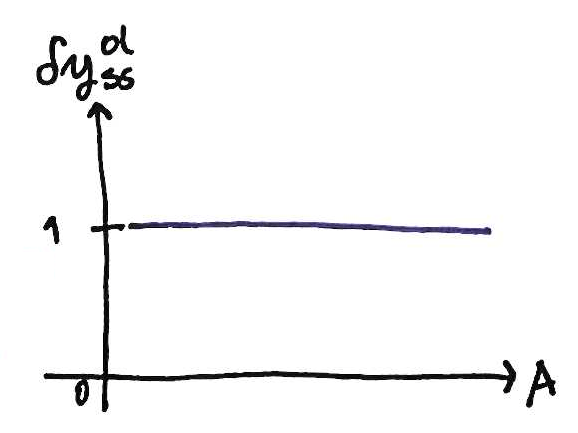
¿Ventaja? Veamos cuál valor final es más sensible.

siempre es 1
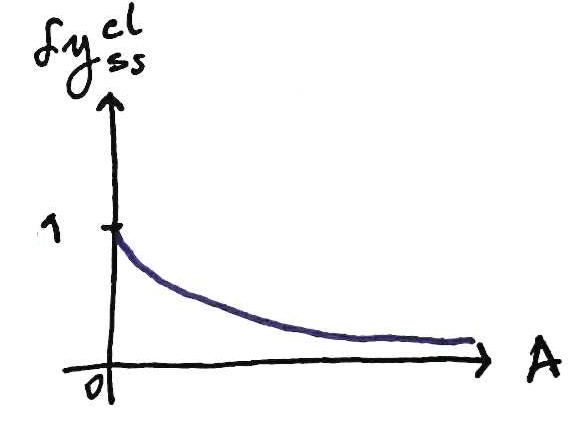
a lo sumo es 1
Menos sensible a errores de modelado
Rechazo de perturbaciones
Problema importante en sistemas de control, como la regulación y el rastreo de referencias.
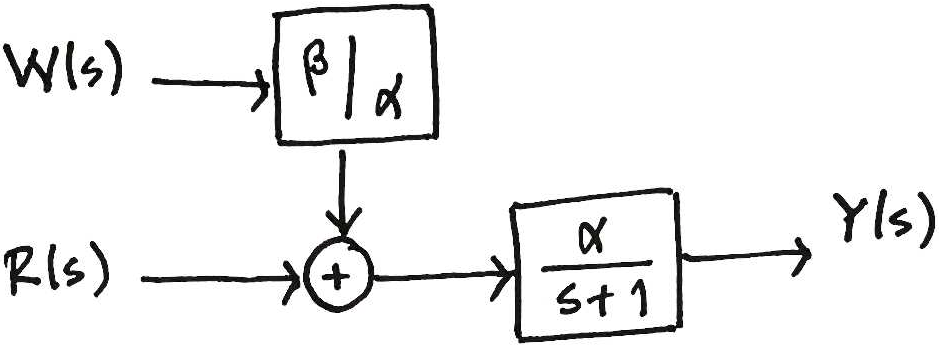
Por superposición:
con \(W(s)=0\)

con \(R(s)=0\)

En lazo cerrado:
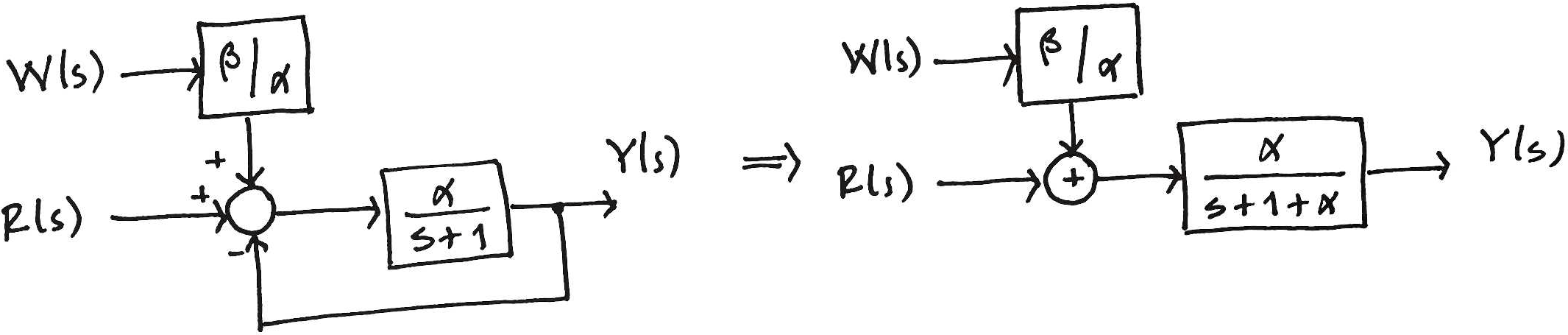
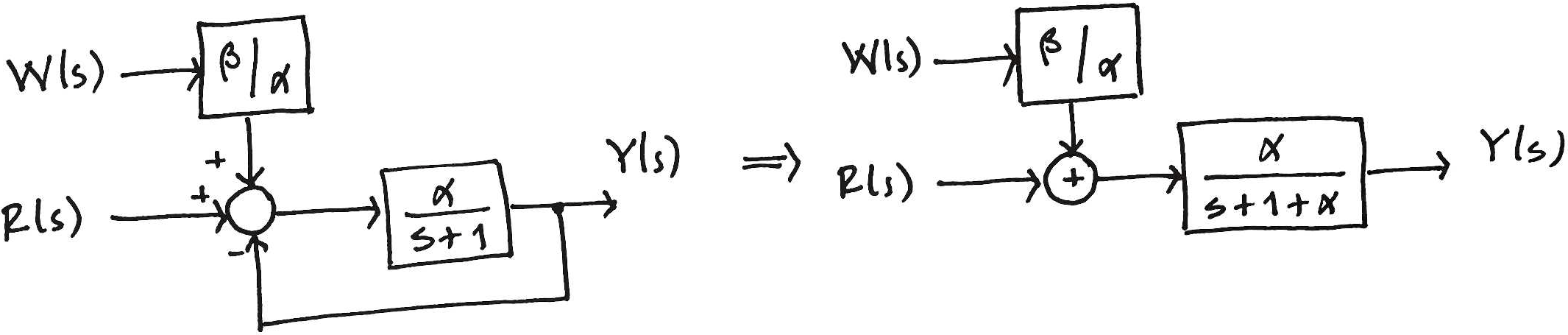
Notar que:
La perturbación afecta en menor medida al sistema en lazo cerrado.
cerrado abierto
Control proporcional
¿Idea de este controlador?
¿Discrepancia entre la salida y la referencia?
¿Idea de este controlador?
¿Discrepancia entre la salida y la referencia?
- Si la desviación de lo deseado con lo obtenido es pequeña, el control es pequeño.
- \(K\) hace que las desviaciones grandes sean suficientes para hacer reaccionar rápidamente al sistema.
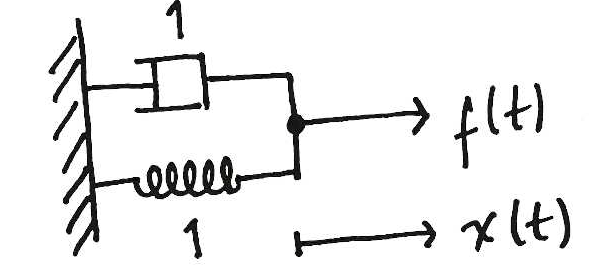
Ejemplo
Objetivos/requerimientos de control:
a) \(\tau=0.1s\) b) \(e_{ss}=0\) c) a) y b) juntos
Ejemplo
Observaciones:
- No podemos obtener más de un objetivo de control de forma exacta.
- No podemos hacer \(e_{ss}=0\) de forma realista.
¿Qué podemos hacer? \(\Rightarrow\) Emplearemos el llamado controlador Proporcional Integral Derivativo (PID).
IE3036 - Lecture 7 (2025)
By Miguel Enrique Zea Arenales
IE3036 - Lecture 7 (2025)
- 21



