IE3036 - Sistemas de Control 1
2do ciclo, 2025
Lección 4: Linealización simple de sistemas no lineales
¿Por qué?
Ejemplo: el péndulo simple
T
\theta
J
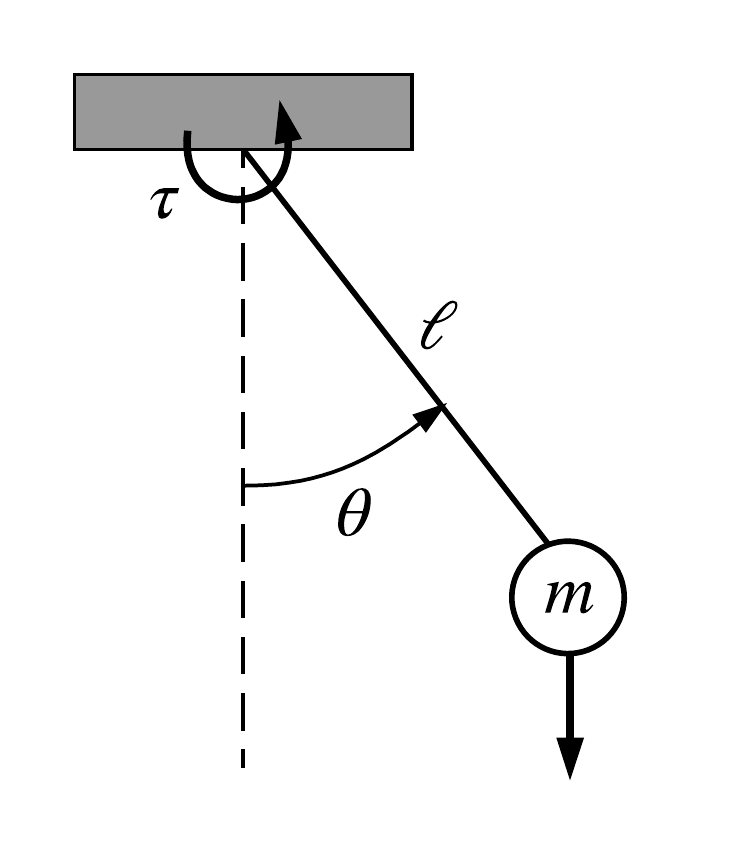
¿Modelo del sistema?
G(s)=\dfrac{\Theta(s)}{\mathrm{T}(s)}
\mathrm{T}(s)=\mathcal{L}\left\{T(t)\right\}=-Mg\ell\mathcal{L}\left\{\sin\left(\theta(t)\right)\right\}
M\ell^2\ddot{\theta}+Mg\ell\sin(\theta)=0
M\ell^2\ddot{\theta}+Mg\ell\sin(\theta) \approx M\ell^2\ddot{\theta}+Mg\ell\theta=0
problema, esta transformada NO existe
este término hace a la EDO no lineal
aproximación de ángulos pequeños
¿Qué tan común es que ocurra esto?
linealización
¿Qué tan común es que ocurra esto?
Linealización local de componentes alrededor de un punto de operación
¿Cuántas funciones lineales vs no lineales podemos graficar en el plano?
f(y)
y
f(y)
y
y_o
f(y_o)
punto de operación
\delta y
\delta f(y)
\text{línea}(y) \approx f(y)
\text{siempre que } y \approx y_o
Si \(y \approx y_o \) entonces podemos aproximar a \(f(y)\) mediante la línea recta:
\delta y = y - y_o
\delta f(y) = f(y) - f(y_o)
Si definimos
f(y) - f(y_o) = m_o (y - y_o)
\Rightarrow \delta f(y) = m_o \delta y
\Rightarrow f(y) \approx m_o \delta y + f(y_o)
(recta que pasa por el origen)
m_o = \left. \dfrac{d f(y)}{dy} \right\vert_{y=y_o}
f(y) \approx \left. \dfrac{d f(y)}{dy} \right\vert_{y=y_o} \underbrace{(y-y_o)}_{\delta y} + f(y_o)
Términos lineales de la expansión por series de Taylor de \(f(y)\) alrededor de \(y_o\)
- Encontramos la no linealidad \(f(y)\).
- Encontramos el punto de operación \(y_o\).
- Aproximamos con la fórmula.
- Transformamos la EDO a las coordenadas linealizadas y se sustituye la aproximación de \(f(y)\).
Procedimiento
Ejemplo: Linealice para pequeñas variaciones alrededor de \(y_o=\pi/4\) y encuentre una (aproximación de la) respuesta del sistema no lineal.
\ddot{y}+2\dot{y}+\cos(y)=0
\ddot{y}+2\dot{y}+\cos(y)=0
G = tf(1, [-2/sqrt(2), -4/sqrt(2), 1]);
[deltay, t] = step(G, 1);
plot(t, deltay + pi/4, 'LineWidth', 1);
Ejemplo: Linealice para pequeñas variaciones alrededor de \(y_o=\pi/4\) y encuentre una (aproximación de la) respuesta del sistema no lineal.
Ejercicio 1
Encuentre la impedancia del componente
+
-
v
i
v=\ln(i)
i_o=1 \text{ A}
Determinando el punto de operación
Si no se provee el punto de operación y este no puede obtenerse mediante algún tipo de análisis en estado estacionario entonces:
- \(y_o=\) referencia del sistema de control (si se tiene esa información).
- \(y_o\) tal que \(f(y_o)=0\) para una selección estratégica de \(f(y)\) (que \(f(y)\) tome en cuenta a todos los términos constantes que no multiplican a \(y\) o sus derivadas).
punto de equilibrio
Si no se provee el punto de operación y este no puede obtenerse mediante algún tipo de análisis en estado estacionario entonces:
- \(y_o=\) referencia del sistema de control (si se tiene esa información).
- \(y_o\) tal que \(f(y_o)=0\) para una selección estratégica de \(f(y)\) (que \(f(y)\) tome en cuenta a todos los términos constantes que no multiplican a \(y\) o sus derivadas).
¿Respuesta al escalón del modelo?
G(s)=\dfrac{\Delta \Theta(s)}{\mathrm{T}(s)}
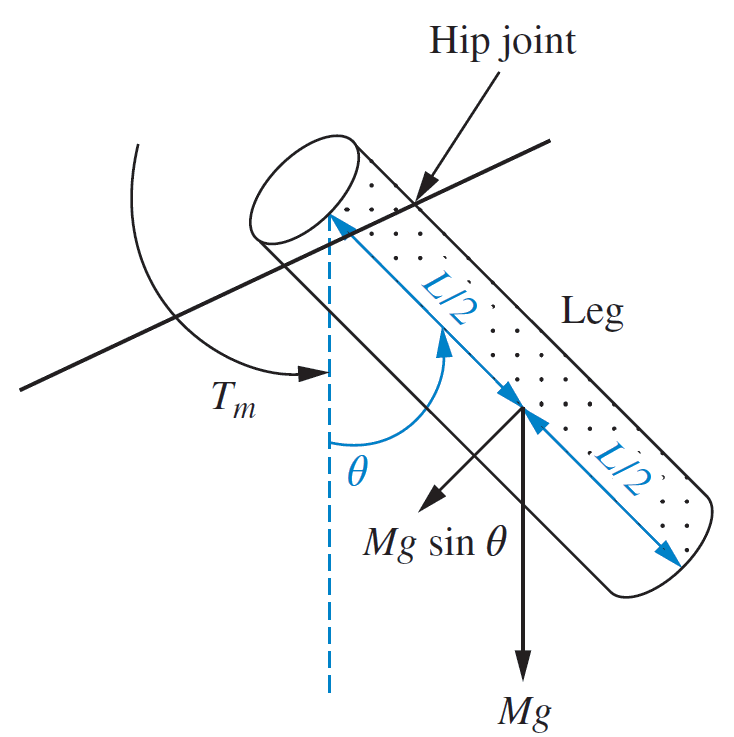
Ejemplo de aplicación
modelo simplificado de una pierna
¿Respuesta al escalón del modelo?
G(s)=\dfrac{\Delta \Theta(s)}{\mathrm{T}(s)}
G(s)=\dfrac{\frac{1}{J}}{s^2 + \frac{D}{J}s + \frac{Mg\ell}{2J}}
modelo simplificado de una pierna
Ejemplo de aplicación
Desafortunadamente MATLAB no puede linealizar directamente el modelo no lineal.
J = 30; D = 10; M = 15; ell = 1; g = 9.81;
G = tf(1/J, [1, D/J, M*g*ell/(2*J)]);
step(G);Desafortunadamente MATLAB no puede linealizar directamente el modelo no lineal.
J = 30; D = 10; M = 15; ell = 1; g = 9.81;
G = tf(1/J, [1, D/J, M*g*ell/(2*J)]);
step(G);pero Simulink sí
De ecuaciones diferenciales a diagramas de bloques
- Se despeja para la derivada más alta.
- Se grafica la secuencia de integradores.
- Se generan los términos asociados a la salida.
- Se combina con la entrada y se cierra el lazo.
Procedimiento
¿Cuál es el diagrama de bloques?
y^{(3)}-2\ddot{y}-5\dot{y}-6y=u
¿Cuál es el diagrama de bloques?
y^{(3)}-2\ddot{y}-5\dot{y}-6y=u
y^{(3)} = 2\ddot{y} + 5\dot{y} + 6y + u
Regresando al ejemplo de aplicación:
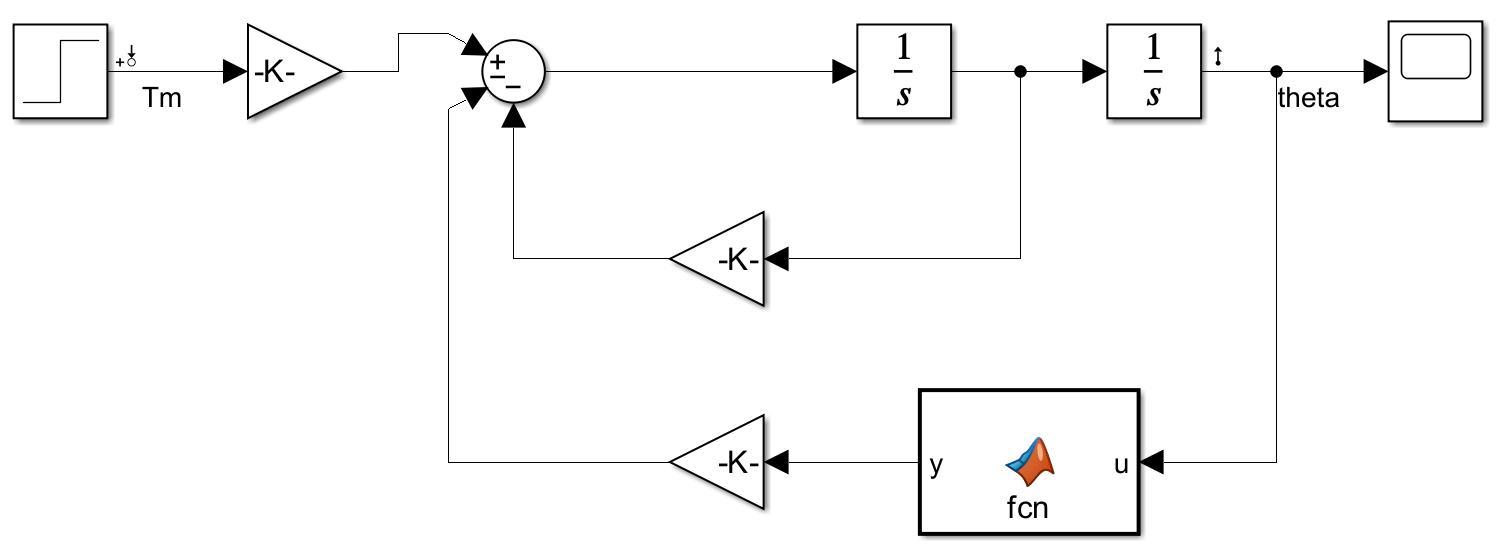
Luego se envía al Model Linearizer
Ejercicio 2
¿Cuál debería ser el punto de operación para la linealización?
\dot{y}+e^{-y}=1
IE3036 - Lecture 4 (2025)
By Miguel Enrique Zea Arenales
