REPETITION

OUTTAKES

Backtracking

Brute force in sensibility but...

...abandoning before exhaustive search

Useful when "dead ends" are recognizable

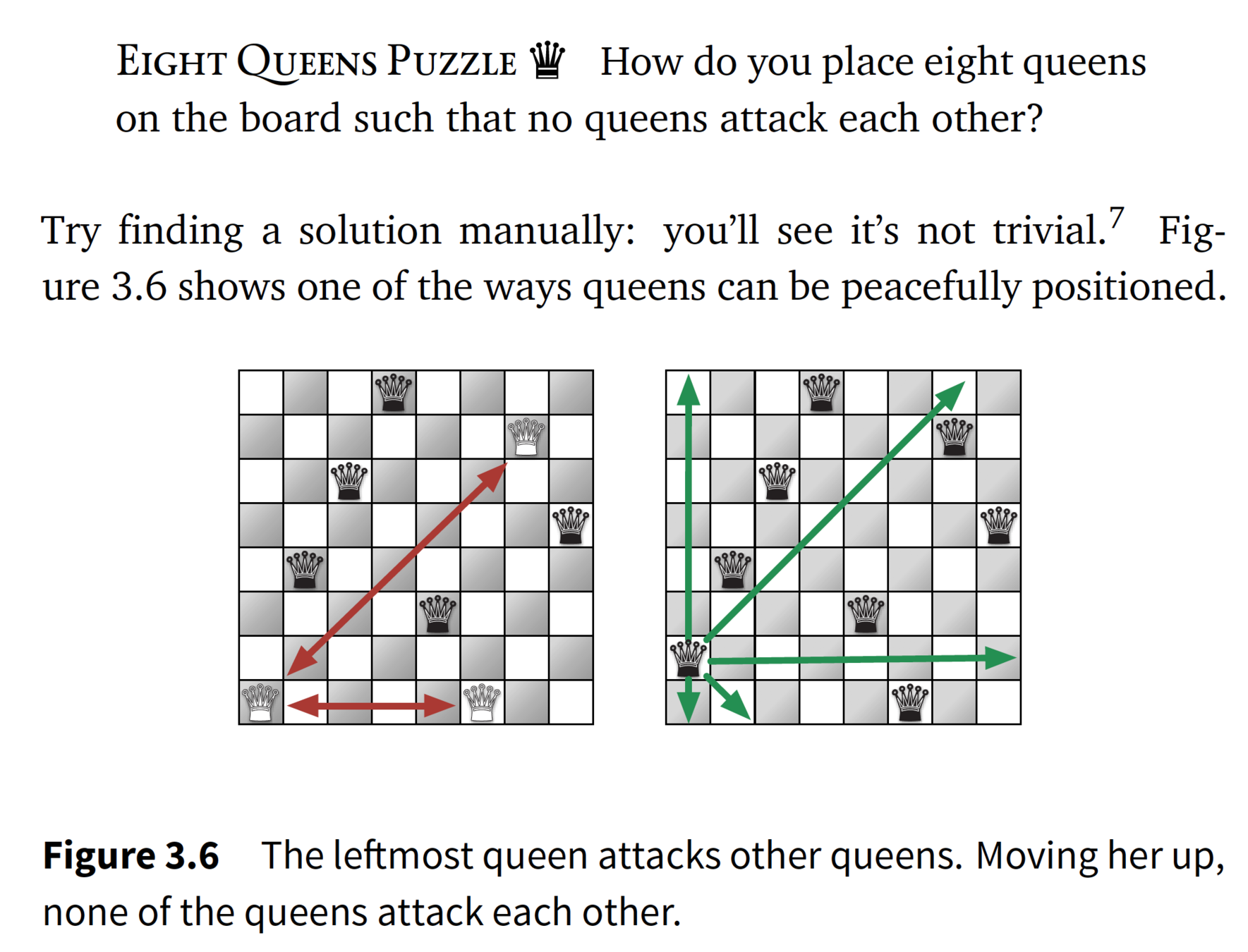
function queens(board)
    if board.has_8_queens //done
        return board
    for each position in board.unattacked_positions  
        //try next open position
        board.place_queen(position)
        //is there a solution from here?
        solution ← queens(board)
        if solution //a returned solution is "true"
           return solution
        //no solution from last placement:backtrack  
        board.remove_queen(position)

    //if all open positions have been tried
    return false

See Also

Finis

Back to Merge Sort

How many mergings?

6 repetitions of 52

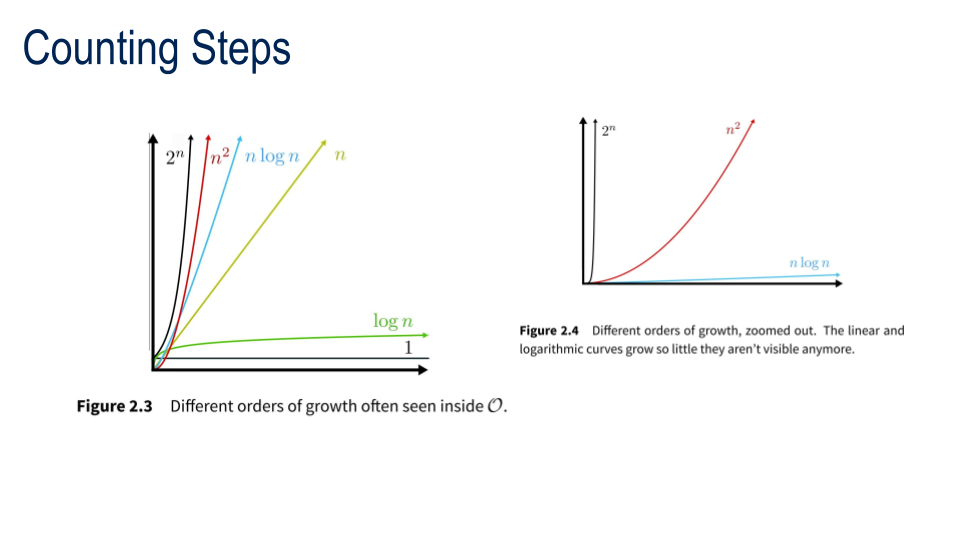
LOG N repetitions of N

NLOGN

Simple Iteration: Merge Sort

Complexity Take Away: Some tasks are a little harder than linear, but not as bad as the next level of complexity.

N log N

WE LIKE THIS.

Chapter 3

Nested Loops

Let's Make Soup

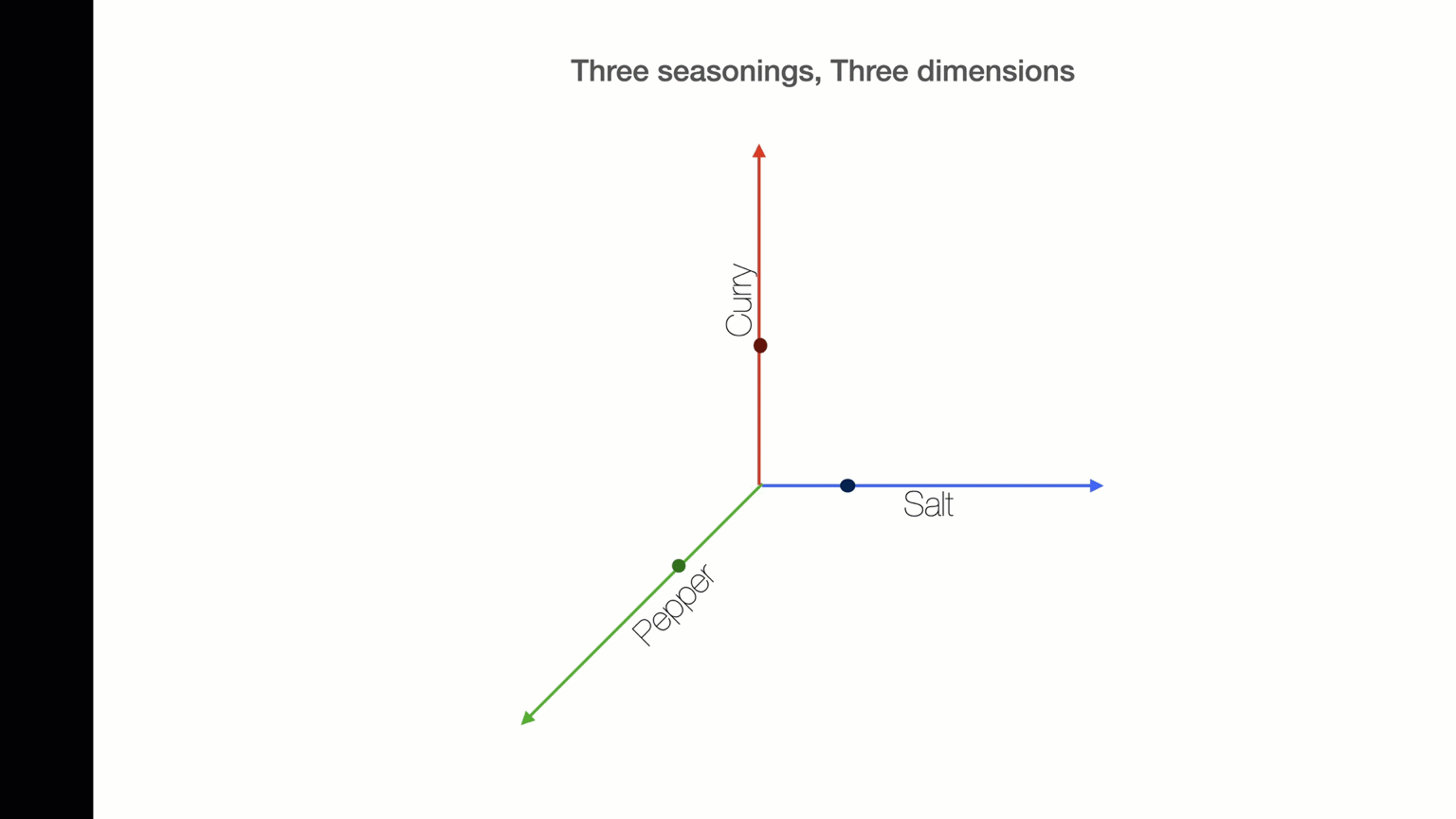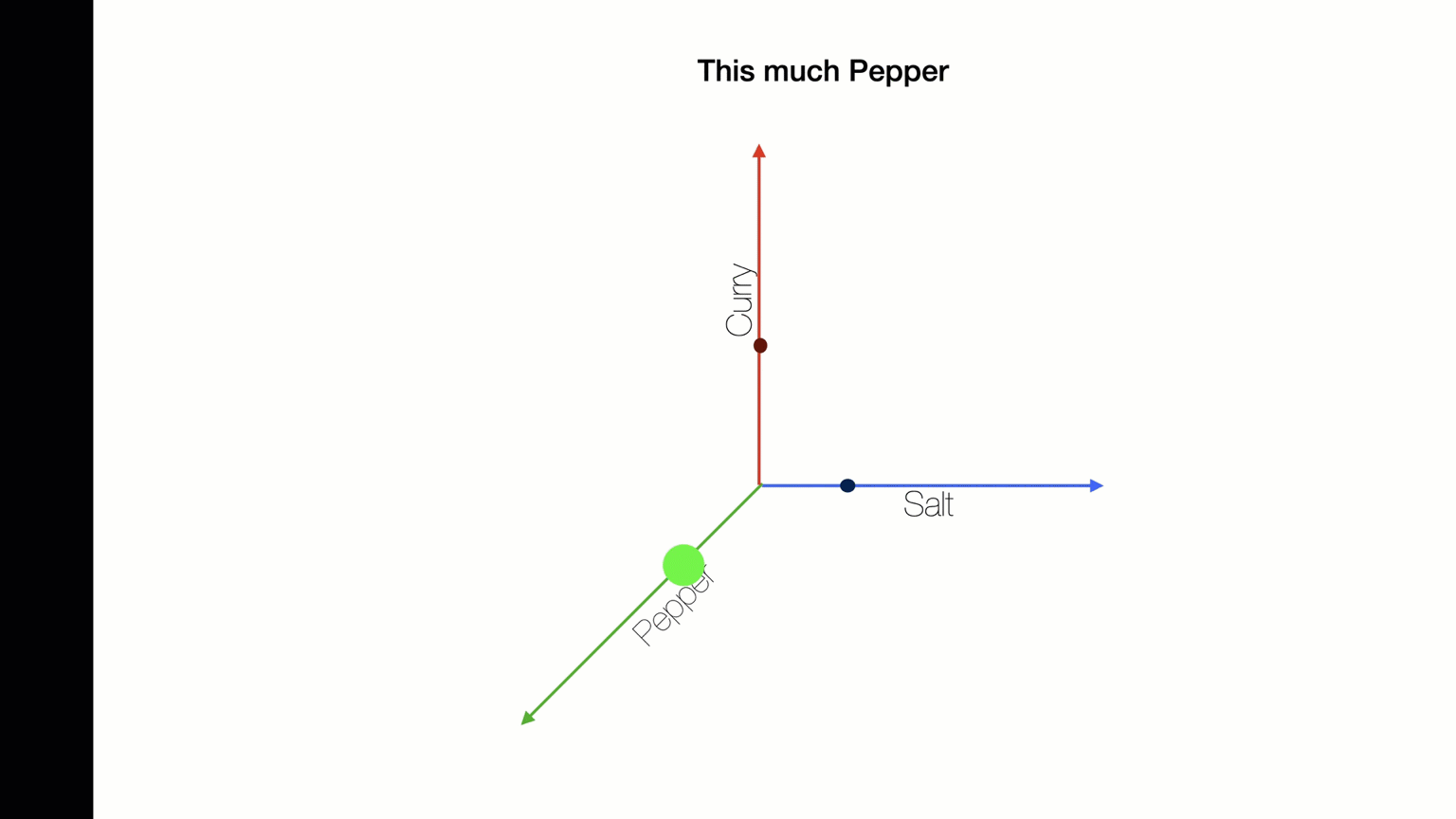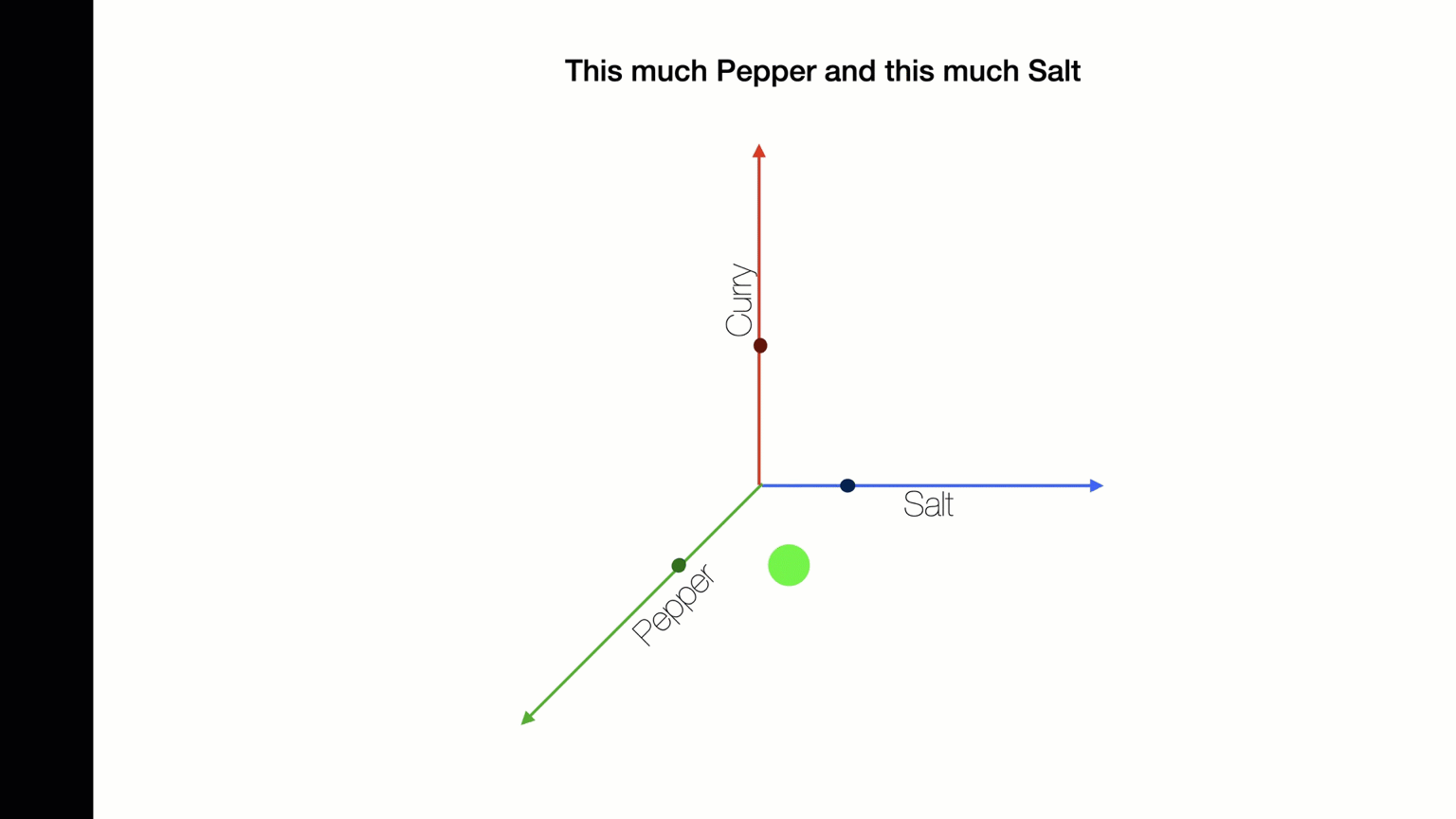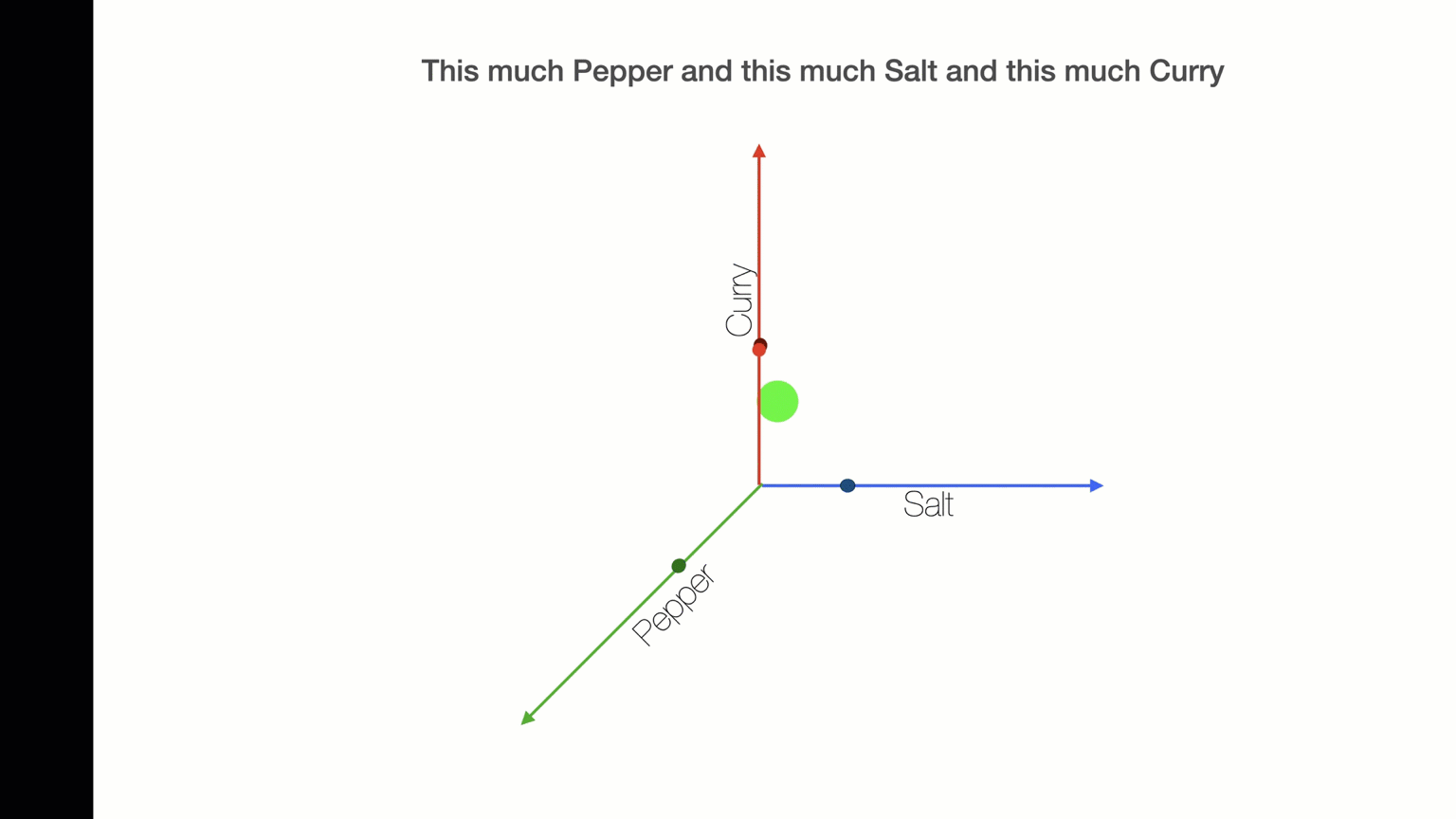
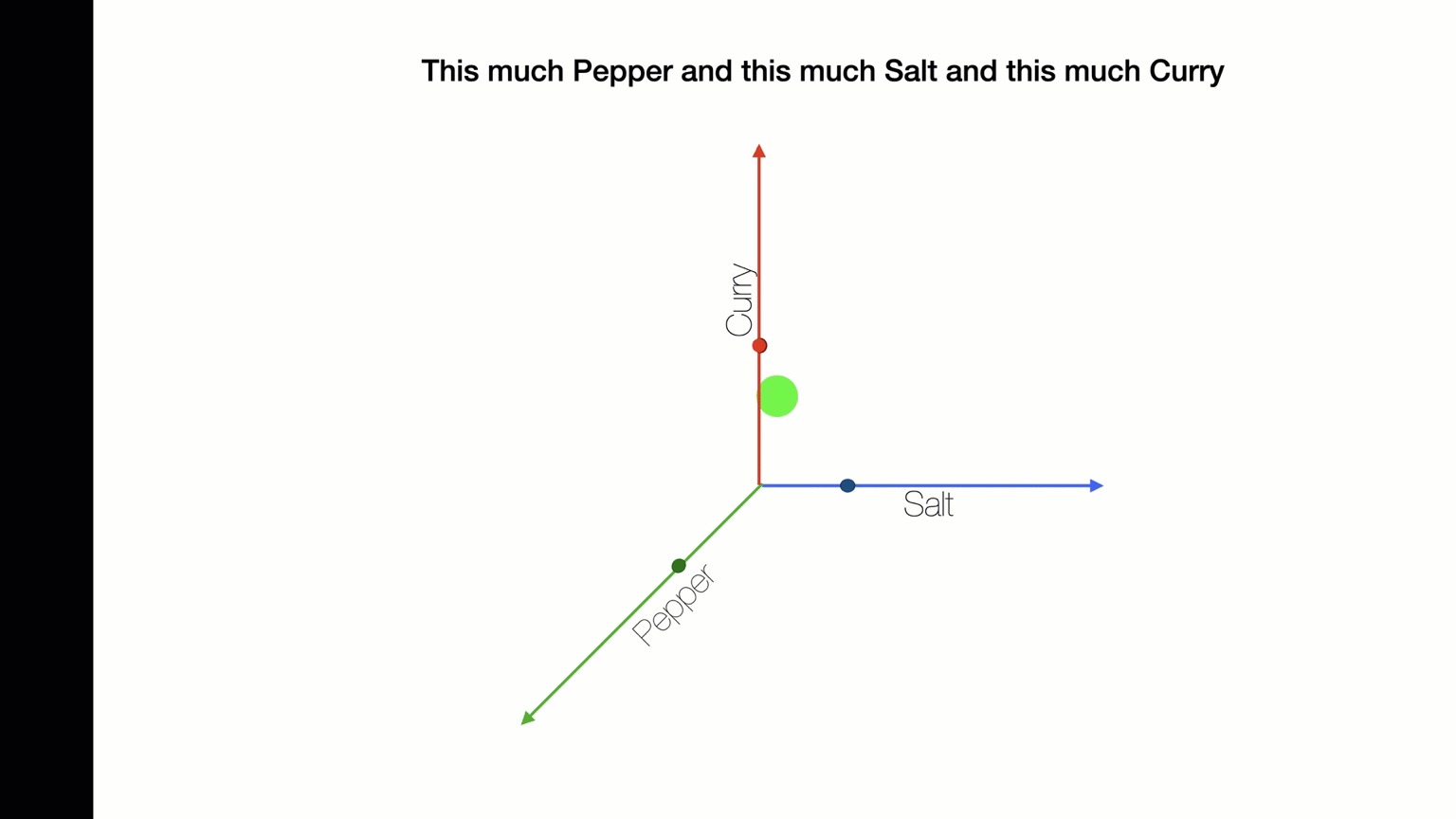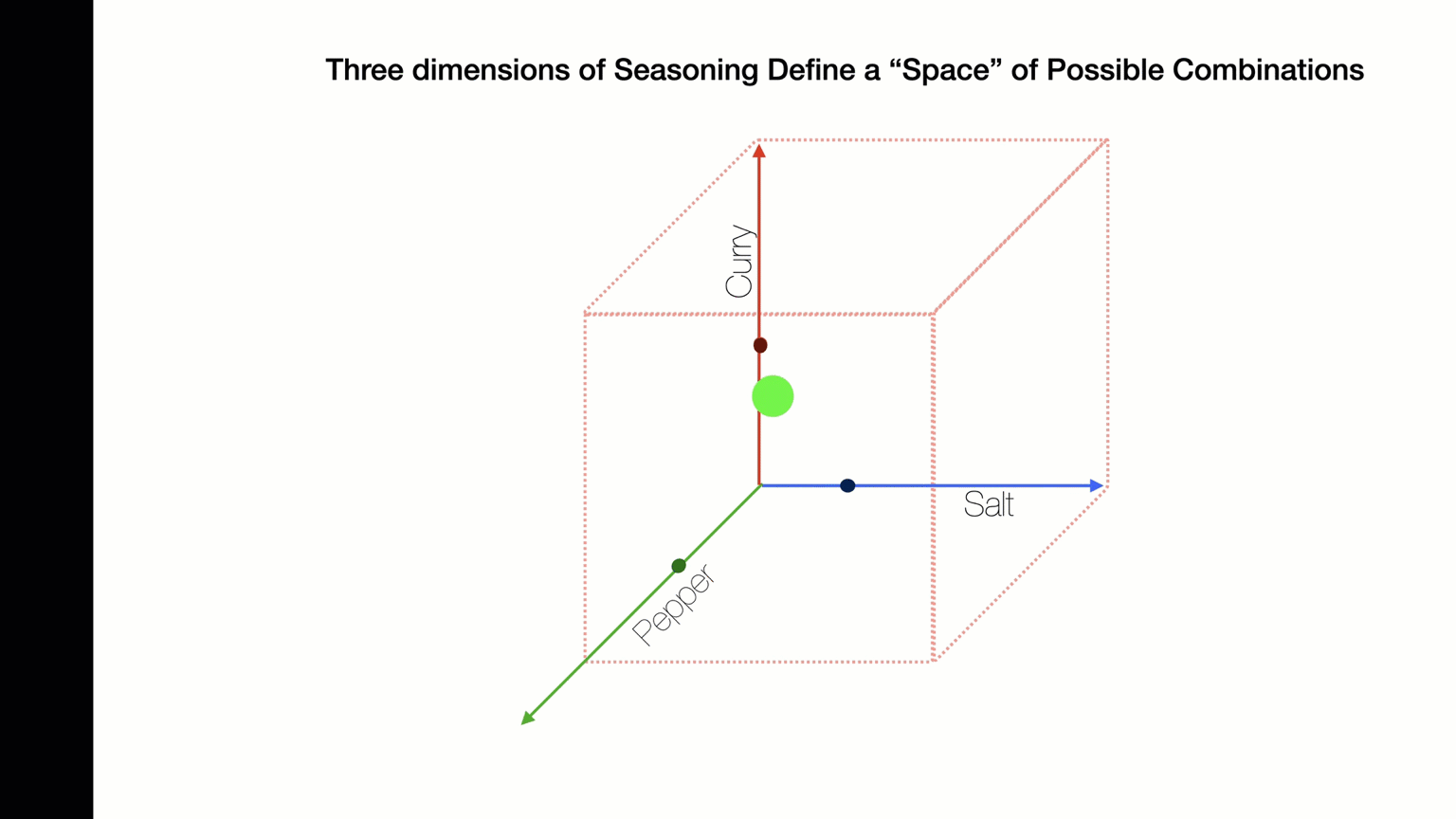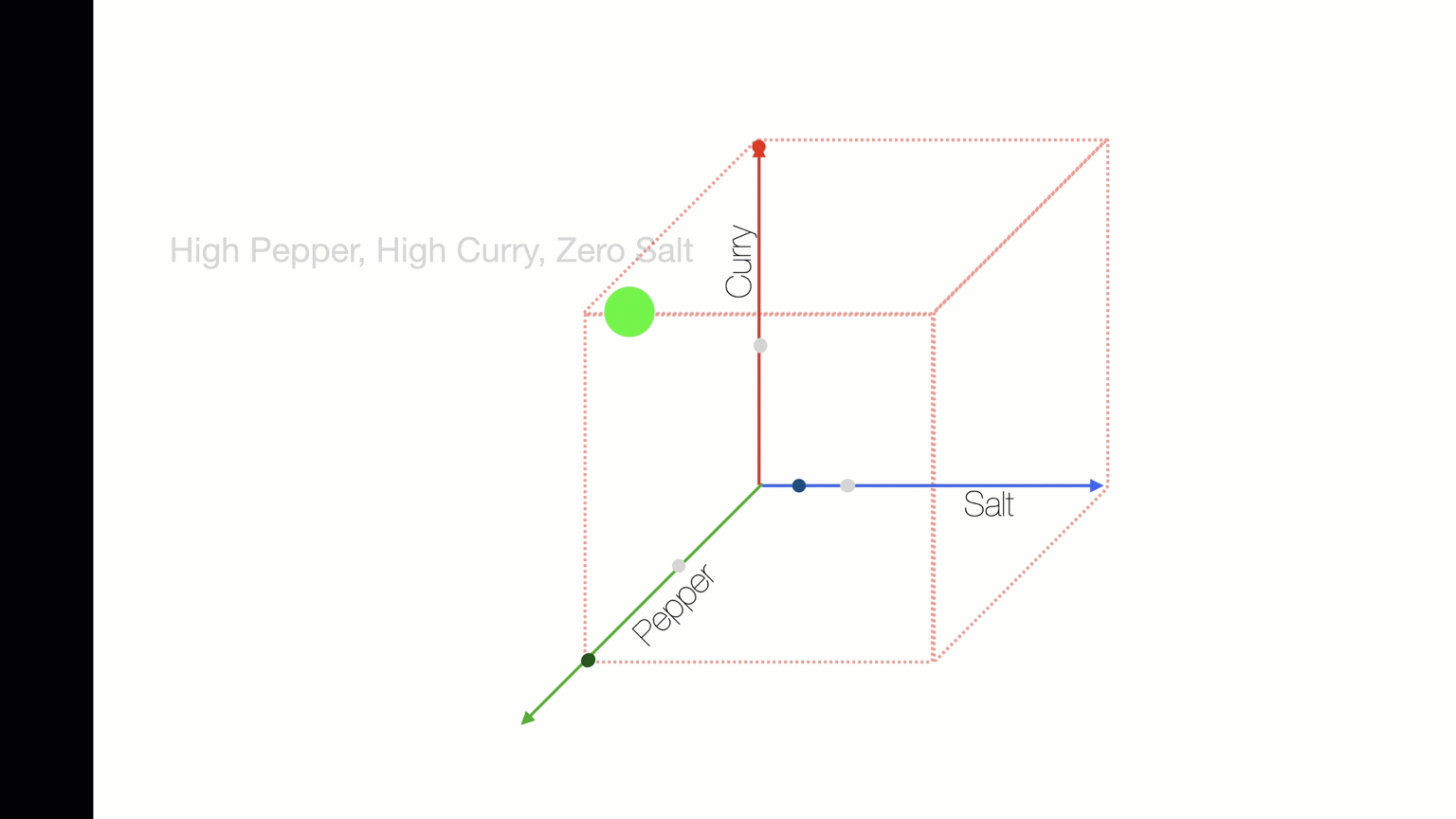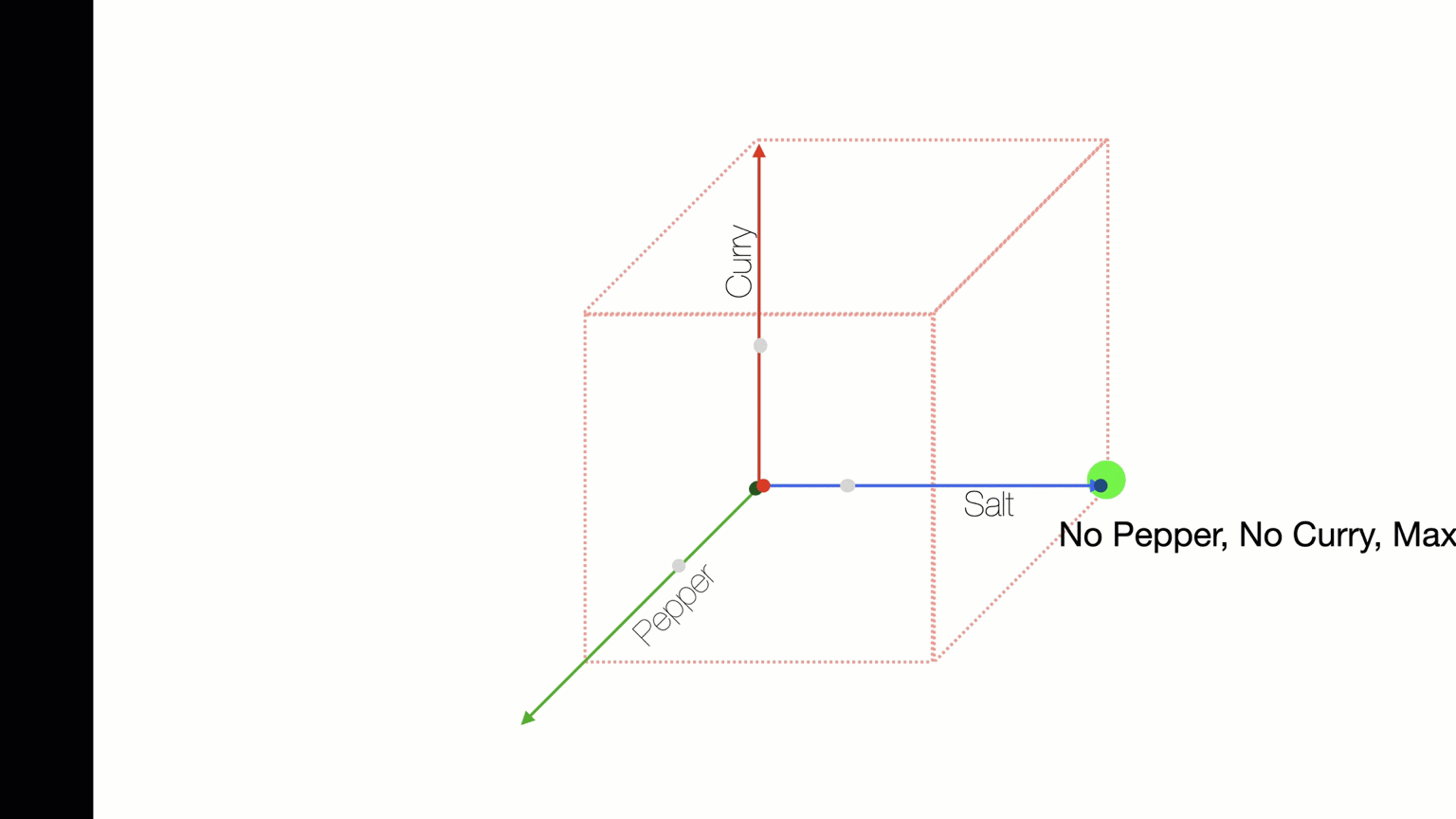
Nested Loops: Stop+Think

Nested Loops: Stop+Think

Nested Loops: Stop+Think

Nested Loops: Stop+Think

Nested Loops: Stop+Think

Chapter 4

This Leads to "Brute Force"

Brute Force

Brute Force

Def: consider every possible solution

Expensive : no clever cost-saving

Skills

Enumerating all the options

Not making it worse

Filho Example

Filho Example

STOP+THINK: What data jig would help us out here?

buyPrices = [10, 9, 7, 11, 10, 9]
sellPrices = [11, 12, 13, 12, 10, 9]

prices = [{"buy":10,"sell":11},

          {"buy":9,"sell":12,

          {"buy":7,"sell":13},

          {"buy":11, "sell":12},

          {"buy":10,"sell":10},

          {"buy":9, "sell":9}]

Filho Example

STOP+THINK: Write the refinement 0 pseudocode.

loop over buy days from 1 to end
   loop over sell days from buy day to end
     compute profit
     track days and amount of best trade

//assume data in array prices
var maxProfit = 0;
var bestBDay  = 0;
var bestSDay  = 0;

for (var bDay = 0; bDay < prices.length; bDay++) {
   for (var sDay = bDay; sDay < prices.length; sDay++) {
      var profit = prices[sDay].sell - prices[bDay].buy
      if (profit > maxProfit) {
         //if best so far, take notes
         maxProfit = profit;
         bestBday = bDay;
         bestSday = sDay;
      }
   }
}
//Prepare results
var result = "Buy on day " + bestBday + " and sell on day " +   
              bestSday + " to realize profit of " + maxProfit

How much computation?

Since we don't have
to compute profit
for sell dates that
are before buy
dates we have this
triangle of numbers
and the number of
computations is
n times n/2.  We would say "on the order of n²."

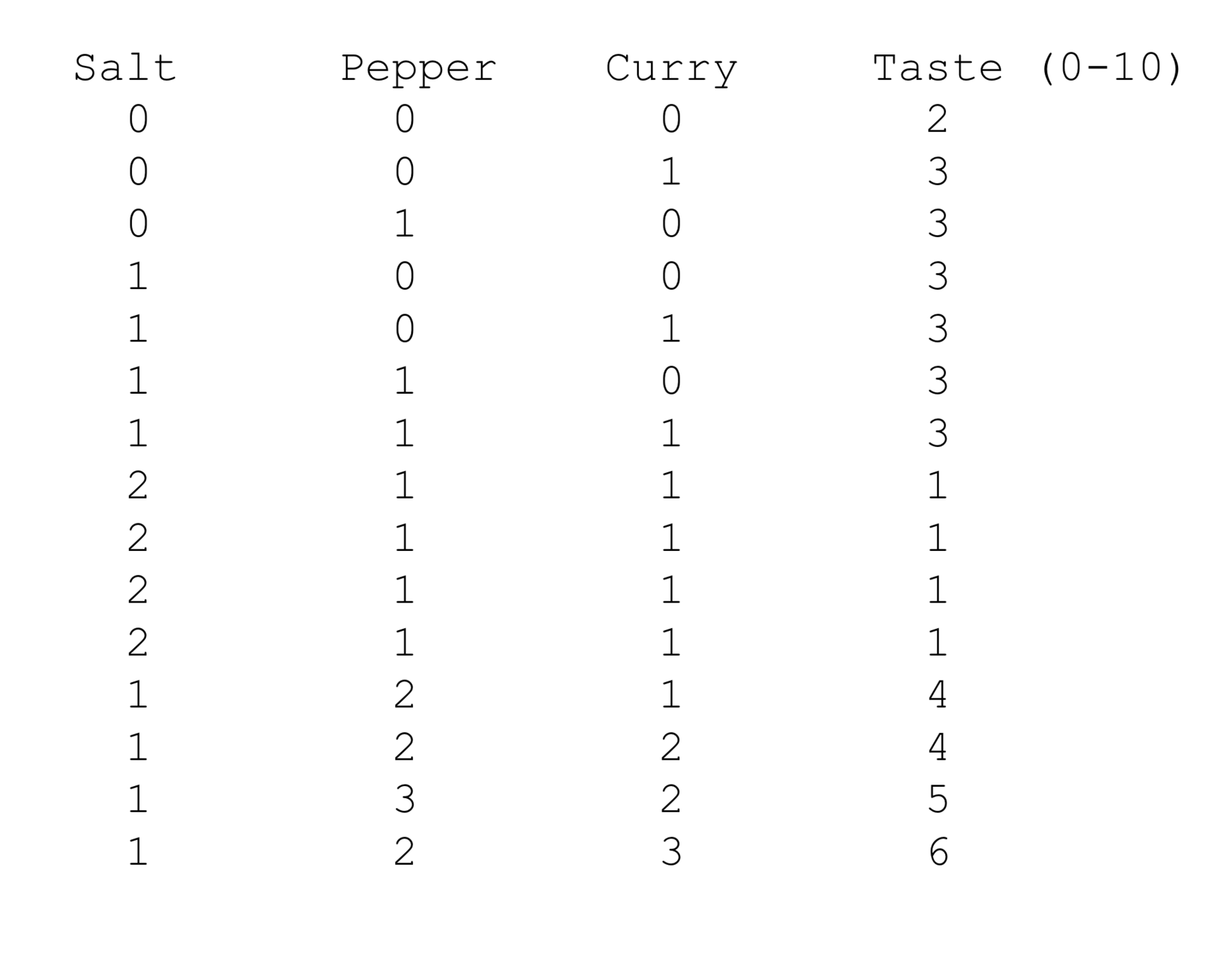
SKILL: Enumerating All the Cases

Outtakes

The merge sort algorithm sorts a list by repeatedly splitting the list in half until reaching pairs or single elements.

If the last step generates a pair, they are put in order and then the sorted pair is returned; otherwise the single is returned.

When the results of a split are returned the two sorted lists are merged.  And then the merged lists are returned and so on and so on.

If we start with 52 cards we split into 26 and 26 and then into 13s and 13s and then into 6s and 7s, and then into 3s and 3s or 3s and 4s, and finally into 2s and 1s.

Complexity Examples

O(1) - determining if a number is odd or even

O(log N) - finding a word in the dictionary

O(N) - reading a book

O(N log N) - merge sorting a deck of playing cards 

O(N^2) - checking combinations of two ingredients

https://stackoverflow.com/questions/7055652/real-world-example-of-exponential-time-complexity

See Also

Introducing Logarithms

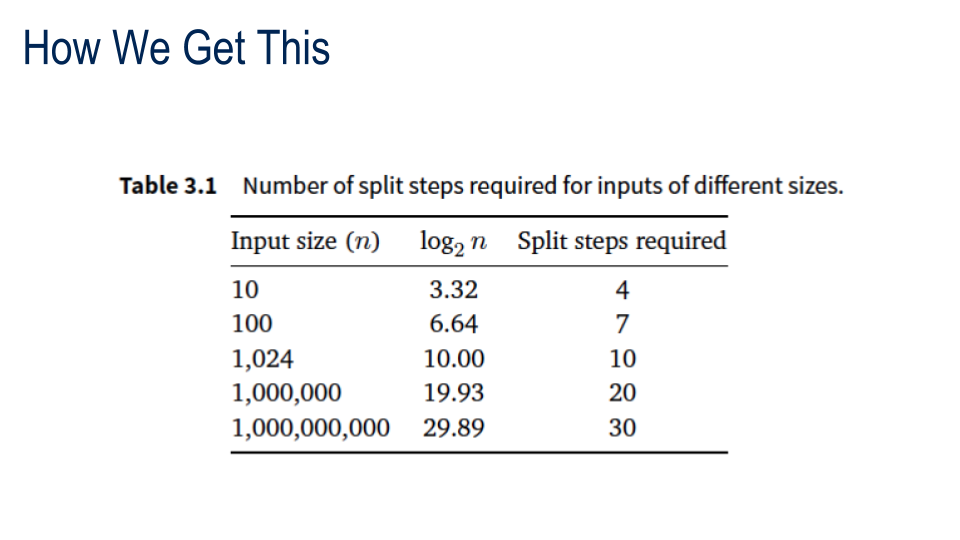
Introducing Logarithms

N > N/2 > N/4 > N/8 > ... 1 and DONE