Christopher Makler
Stanford University Department of Economics
Econ 51: Lecture 5
Specialization and Comparative Advantage
Back to the Edgeworth Box...
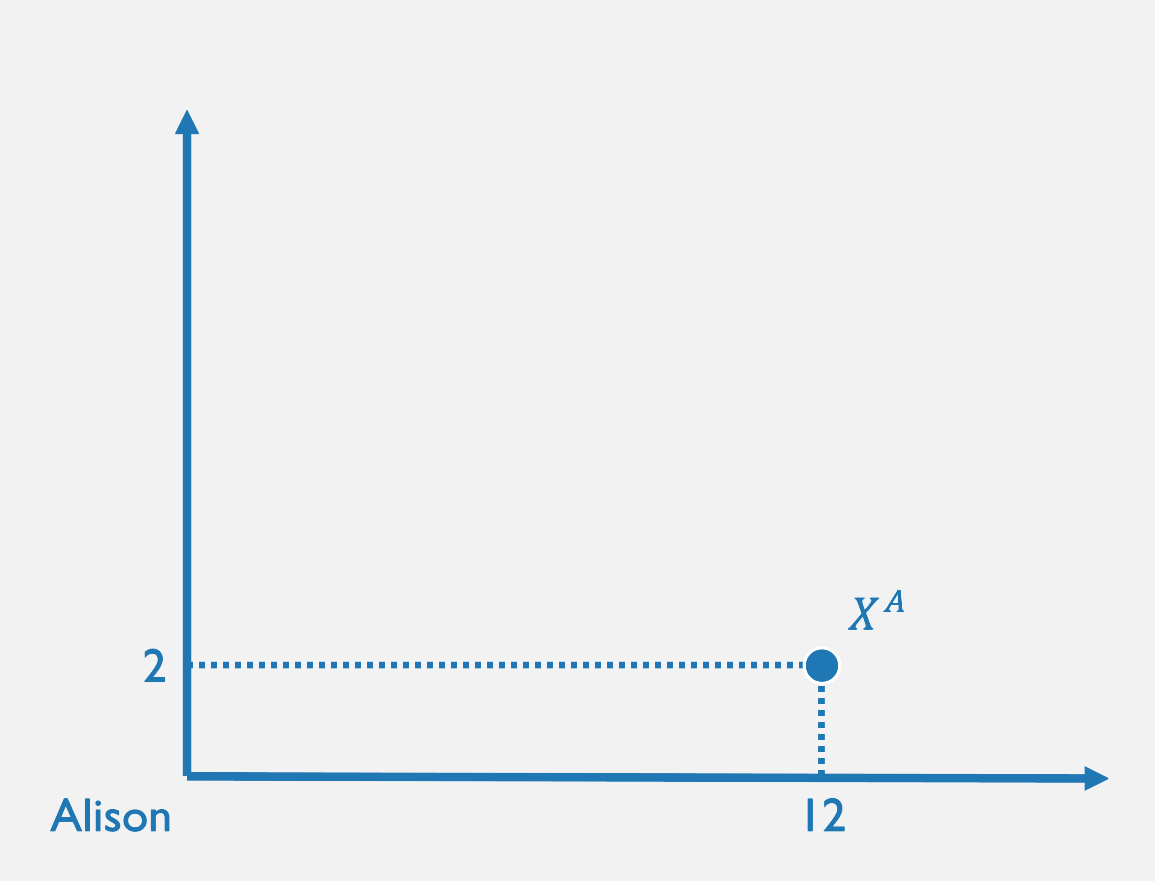
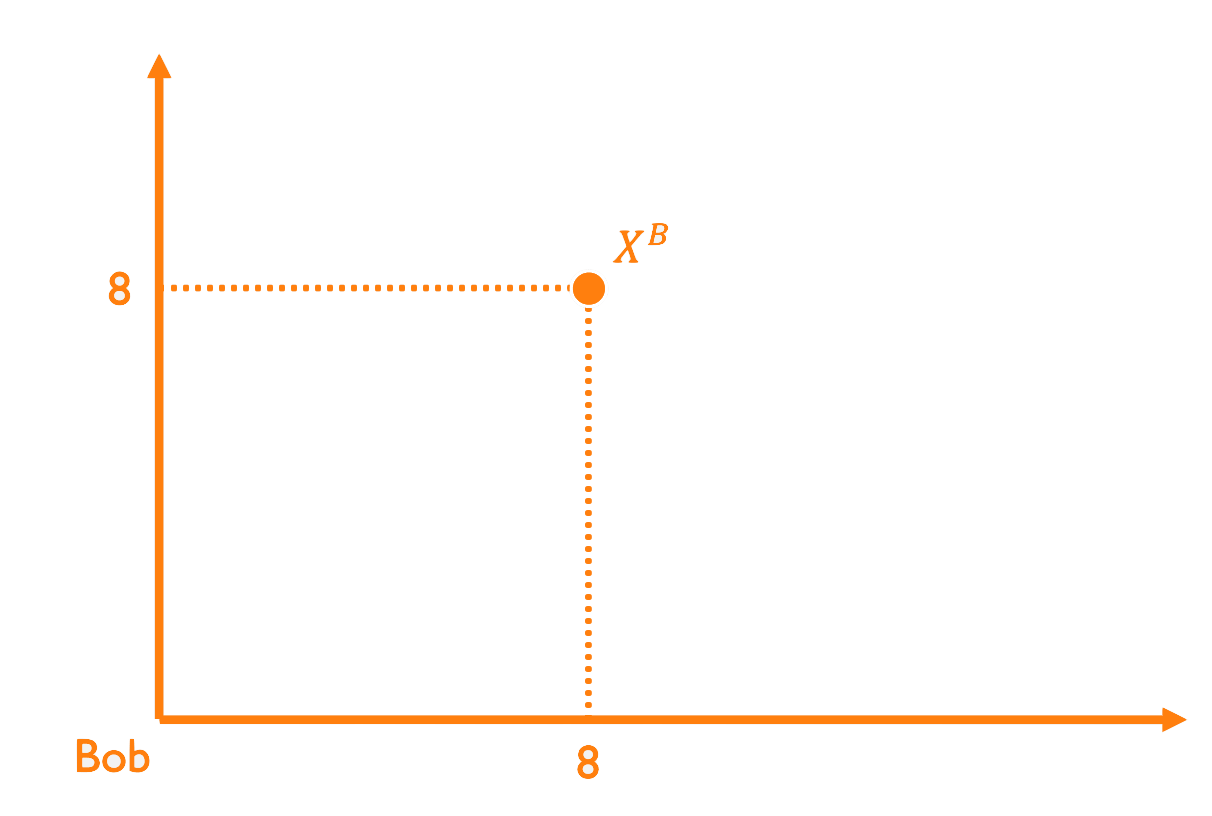
From Bundles to Allocations
From Bundles to Allocations
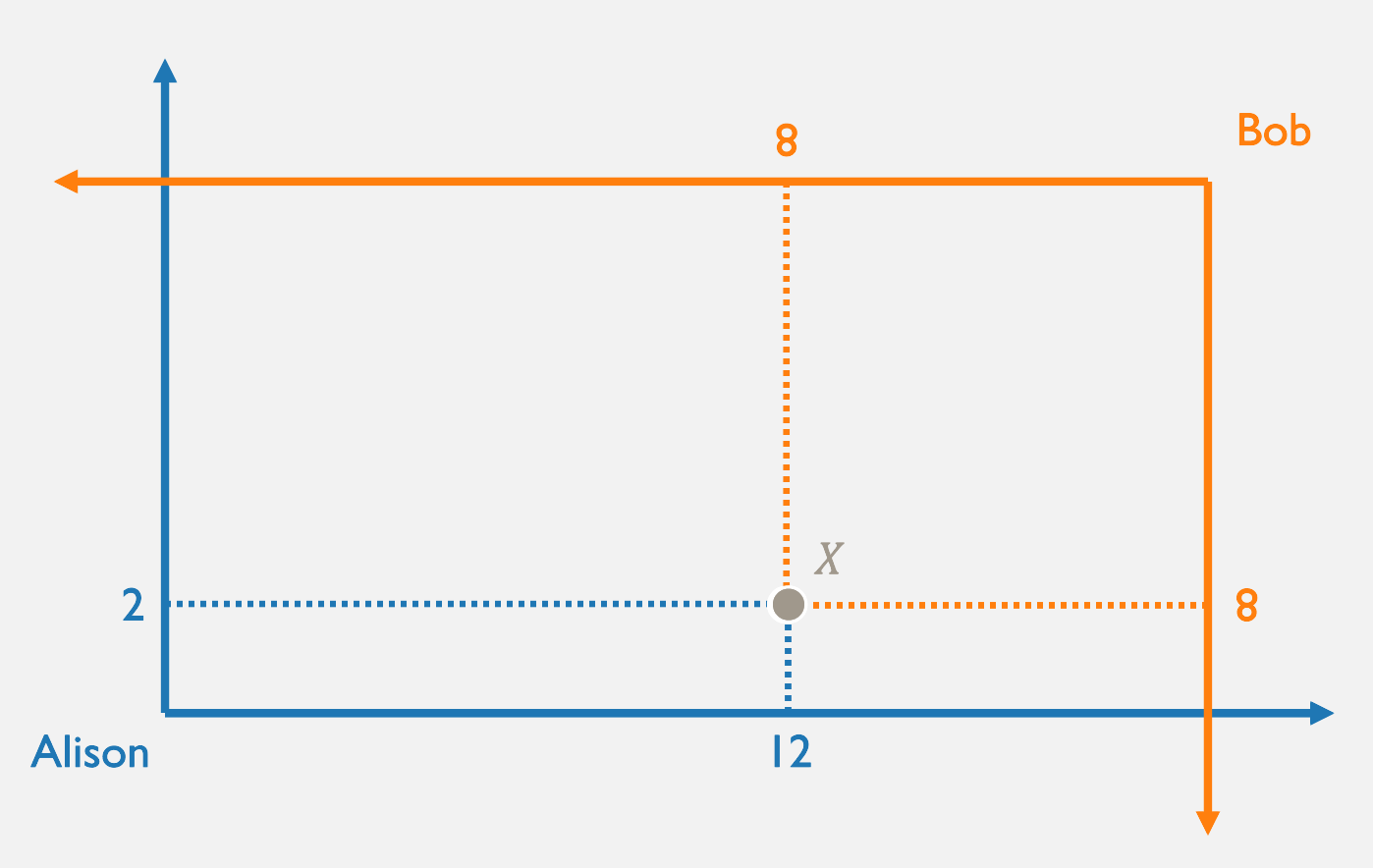
....but where did this "endowment" come from?
Today we will look at production decisions and extend our notion of equilibrium to include production, trade, and consumption.
Today's Agenda
Optimization for an Individual Producer
- Resources constraints and the PPF
- Opportunity Cost and the Marginal Rate of Transformation (MRT)
- Optimization in Autarky
- Buying and selling: specialization and trade from an individual's perspective
Comparative Advantage
- Absolute and Comparative Advantage
- Productive Pareto Efficiency and Specialization
- Competitive Equilibrium with Complete Specialization
Scarcity and Choice
Economics is the study of how
we use scarce resources
to satisfy our unlimited wants
Resources
Goods
Happiness
🌎
⌚️
🤓
Multiple Uses of Resources
Labor
Fish
🐟
Coconuts
🥥
[GOOD 1]
⏳
[GOOD 2]
L_1
L_2
\overline L
Resource Constraint
L_1
L_2
L_1 + L_2 = \overline L
\overline L
\overline L
\text{Total labor available }=\overline L
x_1 = f_1(L_1)
x_2 = f_2(L_2)
Production Possibilities
\text{Fish }(x_1)
\text{Coconuts }(x_2)
Resource Constraint
L_1
L_2
L_1 + L_2 = \overline L
\overline L
\overline L
\text{Total labor available }=\overline L
\text{(Good 1 - Good 2 space)}
x_1 = f_1(L_1)
x_2 = f_2(L_2)
f_1(\overline L)
f_2(\overline L)
Example:
\overline L = 12
f_1(L_1) = 2L_1
f_2(L_2) = L_2
RESOURCE CONSTRAINT
PRODUCTION FUNCTIONS
Example:
\overline L = 12
f_1(L_1) = 2L_1
f_2(L_2) = L_2
RESOURCE CONSTRAINT
PRODUCTION FUNCTIONS
How do we draw the PPF?
Method 1: Plot points
L_1
L_2
0
12
6
6
12
0
x_1
0
x_2
12
12
24
6
0
\text{Fish }(x_1)
\text{Coconuts }(x_2)
6
12
18
24
0
0
6
12
18
24
Example:
\overline L = 12
f_1(L_1) = 2L_1
f_2(L_2) = L_2
RESOURCE CONSTRAINT
PRODUCTION FUNCTIONS
How do we draw the PPF?
Method 2: Derive equation
\text{Fish }(x_1)
\text{Coconuts }(x_2)
6
12
18
24
0
0
6
12
18
24
L_1 + L_2 = 12
x_1 = 2L_1
Want to write in terms of \(x_1\) and \(x_2\)...
x_2 = L_2
L_1 = \tfrac{1}{2}x_1
L_2 = x_2
\tfrac{1}{2}x_1 + x_2 = 12
Slope of the PPF:
Marginal Rate of Transformation (MRT)
Rate at which one good may be “transformed" into another
...by reallocating resources from one to the other.
Opportunity cost of producing an additional unit of good 1,
in terms of good 2
Note: we will generally treat this as a positive number
(the magnitude of the slope), just like with did with MRS and the price ratio.
\overline L = 12
f_1(L_1) = 2L_1
f_2(L_2) = L_2
RESOURCE CONSTRAINT
PRODUCTION FUNCTIONS
\text{Fish }(x_1)
\text{Coconuts }(x_2)
6
12
18
24
0
0
6
12
18
24
\tfrac{1}{2}x_1 + x_2 = 12
Finding the MRT
\displaystyle{MRT = \left|{dx_2 \over dx_1}\right| = {1 \over 2}}
It takes \({1 \over 2}\) of an hour (30 minutes)
to make another
unit of good 1
It takes 1 hour to make another
unit of good 2
If you spend 30 more minutes to make another unit of good 1, how much good 2 could you have made in that same 30 minutes?
Suppose we're allocating 3 hours of labor to fish (good 1),
and 9 to coconuts (good 2).
Now suppose we shift
one hour of labor
from coconuts to fish.
How many fish do we gain?
\Delta_2
\Delta_1
9
8
6
8
How many coconuts do we lose?
\Delta_2 = MP_{L_2} = 1\text{ coconut}
\Delta_1 = MP_{L_1} = 2\text{ fish}
\left|\text{slope}\right| = \frac{MP_{L_2}}{MP_{L_1}}
Relationship between MPL's and MRT
x_1 = f_1(L_1) = 2L_1
x_2 = f_2(L_2) = L_2
Fish production function
Coconut production function
Resource Constraint
L_1 + L_2 = 150
PPF
pollev.com/chrismakler
Suppose Chuck can use labor
to produce fish (good 1)
or coconuts (good 2).
If we plot his PPF in good 1 - good 2 space, what are the units of Chuck's MRT?
Suppose Chuck could initially produce 3 fish (good 1) or 2 coconuts (good 2)
in an hour.
He gets better at fishing, which allows him to produce 4 fish per hour.
What effect will this have on his MRT?
CHECK YOUR UNDERSTANDING
pollev.com/chrismakler
Optimization in Autarky
Marginal Rate of Transformation (MRT)
- The number of coconuts you need to give up in order to get another fish
- Opportunity cost of fish in terms of coconuts
Marginal Rate of Substitution (MRS)
- The number of coconuts you are willing to give up in order to get another fish
- Willingness to "pay" for fish in terms of coconuts
Both of these are measured in
coconuts per fish
(units of good 2/units of good 1)
Marginal Rate of Transformation (MRT)
- The number of coconuts you need to give up in order to get another fish
- Opportunity cost of fish in terms of coconuts
Marginal Rate of Substitution (MRS)
- The number of coconuts you are willing to give up in order to get another fish
- Willingness to "pay" for fish in terms of coconuts
Opportunity cost of marginal fish produced is less than the number of coconuts
you'd be willing to "pay" for a fish.
Opportunity cost of marginal fish produced is more than the number of coconuts
you'd be willing to "pay" for a fish.
Better to spend less time fishing
and more time making coconuts.
Better to spend more time fishing
and less time collecting coconuts.
MRS
>
MRT
MRS
<
MRT
Utility of spending
another hour producing fish
Utility value of spending
another hour producing coconuts
MP_{L1}
=
Optimize by setting them equal to one another
\times
MU_1
MP_{L2}
\times
MU_2
MP_{L1}
=
Optimize by setting them equal to one another
MU_1
MP_{L2}
MU_2
MRS =
= MRT
Solving for the Optimal Bundle
Chuck has 12 hours of labor, and can produce 2 coconuts per hour or 1 fish per hour.
His preferences may be represented by the utility function \(u(x_1,x_2) = x_1x_2^2\)
\text{s.t. }
\mathcal{L}(x_1,x_2,\lambda)=
\displaystyle{\max_{x_1,x_2}}
x_1x_2^2
12 - {1 \over 2}x_1 - x_2
+ \lambda\ (
)
OBJECTIVE
FUNCTION
CONSTRAINT
x_1x_2^2
12 - {1 \over 2}x_1 - x_2 = 0
{1 \over 2}x_1 + x_2 = 12
UTILS
HOURS
What are the units?
UTILS
PER
HOUR
\mathcal{L}(x_1,x_2,\lambda)=
x_1x_2^2
12 - {1 \over 2}x_1 - x_2
+ \lambda\ (
)
\displaystyle{\partial \mathcal{L} \over \partial x_1} =
FIRST ORDER CONDITIONS
\displaystyle{\partial \mathcal{L} \over \partial x_2} =
\displaystyle{\partial \mathcal{L} \over \partial \lambda} =
x_2^2
2x_1x_2
12 - {1 \over 2}x_1 - x_2
=0
- \lambda\ \times
{1 \over 2}
1
- \lambda\ \times
=0
=0
\displaystyle{\Rightarrow \lambda\ = \ \ \ \ \ \ \ \ \ \ \ \times}
{1 \over 2}x_1 + x_2 = 12
\displaystyle{\Rightarrow \lambda\ = \ \ \ \ \ \ \ \ \ \ \ \times}
x_2^2
2x_1x_2
2
1
MU_1
MU_2
MP_{L1}
MP_{L2}
\Rightarrow
Utility from last hour spent fishing
Utility from last hour spent collecting coconuts
Equation of PPF
\displaystyle{\lambda\ = \ \ \ \ \ \ \ \ \ \ \ \times}
{1 \over 2}x_1 + x_2 = 12
\displaystyle{ = \ \ \ \ \ \ \ \ \ \ \ \times}
x_2^2
2x_1x_2
2
1
MU_1
MU_2
MP_{L1}
MP_{L2}
Utility from last hour spent fishing
Utility from last hour spent collecting coconuts
Equation of PPF
=
x_2^2
2x_1x_2
2
1
MU_1
MU_2
MP_{L1}
MP_{L2}
Equation of PPF
TANGENCY
CONDITION
MRS
MRT
CONSTRAINT
{1 \over 2}x_1 + x_2 = 12
{1 \over 2}x_1 + x_2 = 12
=
x_2^2
2x_1x_2
2
1
x_2 = x_1
{1 \over 2}x_1 + \ \ \ \ \ = 12
x_1
{3 \over 2}x_1 = 12
x_1^* = 8
x_2^* = 8
TANGENCY
CONDITION
CONSTRAINT
PLUG INTO
CONSTRAINT
PLUG BACK INTO TANGENCY CONDITION
x_1^*(p_1,p_2,m) = \frac{a}{a+b}\times \frac{m}{p_1}
For a Cobb-Douglas utility function of the form
Recall: The “Cobb-Douglas Rule"
u(x_1,x_2) = x_1^ax_2^b
The demand functions will be
x_2^*(p_1,p_2,m) = \frac{b}{a+b}\times \frac{m}{p_2}
That is, the consumer will spend fraction \(a/(a+b)\) of their income on good 1, and fraction \(b/(a+b)\) of their income on good 2.
This shortcut is very much worth memorizing! We'll use it a lot in the next few weeks in place of going through the whole optimization process.
For a Cobb-Douglas utility function of the form
The “Cobb-Douglas Rule" for Production
u(x_1,x_2) = x_1^ax_2^b
the producer/consumer will optimally spend fraction \(a/(a+b)\) of their total resource value on good 1, and fraction \(b/(a+b)\) on good 2.
Example: Chuck has 12 hours of labor, and can produce 2 coconuts per hour or 1 fish per hour.
His preferences may be represented by the utility function \(u(x_1,x_2) = x_1x_2^2\)
What does the Cobb-Douglas rule say he should do?
pollev.com/chrismakler
Suppose Chuck's utility function was
\(u(x_1,x_2) = 3x_1 + 4x_2\).
What would his optimal choice have been?
Equation of PPF
{1 \over 2}x_1 + x_2 = 12
Specialization and Trade
Now suppose Chuck can buy and sell these goods at prices \(p_1\) and \(p_2\).
\text{Monetary value of }(y_1,y_2)=p_1y_1 + p_2y_2
Notation: \(y_i\) is the amount he produces of good \(i\); \(x_i\) is the amount he consumes.
Money from spending
another hour producing fish
Money from spending
another hour
producing coconuts
MP_{L1}
\times
p_1
MP_{L2}
\times
p_2
With linear production functions, he should completely specialize in one or the other!
Two Agents
\overline L = 12
f_1(L_1) = 2L_1
f_2(L_2) = L_2
CHUCK
\overline L = 12
f_1(L_1) = 3L_1
f_2(L_2) = 3L_2
WILSON
DEFINITIONS
Absolute advantage: the ability to produce a good using fewer resources.
Comparative advantage: the ability to produce a good at a lower opportunity cost.
Productive Efficiency
Allocative Efficiency
You cannot reallocate goods
and make someone better off
without making someone else worse off.
You cannot reallocate resources
and produce more of one good
without making less of another good.
How to construct a joint PPF
- Start from the vertical intercept: its value is the quantity produced of good 2 if everyone completely specializes in good 2.
- As you increase good 1, think about who should produce each unit of the good.
- Continue until you hit the horizontal axis, at the point where everyone specializes in good 1.
- (It's pretty simple with two people and linear PPFs, but there are more complicated ones...)
Solving for Equilibrium I: Production
We know that Chuck and Wilson have different opportunity costs of producing fish:
MRT = {1 \over 2}
CHUCK
MRT = 1
WILSON
For what range of price ratios will each of them specialize in the good for which they have a comparative advantage?
Solving for Equilibrium II: Trade
Once everyone is specializing, we have the endowments:
(24,0)
CHUCK
(0,36)
WILSON
How much fish will each supply and demand at different prices?
u(x_1,x_2) = x_1x_2^2
Suppose both Chuck and Wilson have
Cobb-Douglas preferences given by
(24,0)
CHUCK
(0,36)
WILSON
u(x_1,x_2) = x_1x_2^2
Let's fix \(p_2 = 1\) and solve for \(p_1\).
VALUE OF ENDOWMENT
\hat m^A = 24p_1
\hat m^B = 36
OPTIMAL CHOICE
x_1^A = 8
x_1^B = {12 \over p_1}
x_1^* = {\hat m \over 3p_1}
SUPPLY AND DEMAND
s_1^A(p_1) = 16
d_1^B(p_1) = {12 \over p_1}
p_1^* = {3 \over 4}
Next time: we finish our 13-week investigation of the neoclassical model...
Econ 51 | 05 | Comparative Advantage
By Chris Makler
Econ 51 | 05 | Comparative Advantage
Comparative Advantage and the Gains from Trade
