\text{Chapter 11}
\text{Chapter 11}
\text{Chapter 11}
\text{Chapter 11}
\begin{align*}
&\text{A uniform wheel of radius } 0.5\,\text{m rolls without slipping on a horizontal surface.} \\
&\text{Starting from rest, the wheel moves with constant angular acceleration } \\
&6.0\,\text{rad/s}^2. \\
&\text{The distance traveled by the center of mass of the wheel from } t=0 \text{ to } t=3\,\text{s is:} \\
\\
&\text{A) } 0 \text{ m} \\
&\text{B) } 27 \text{ m} \\
&\text{C) } 13.5 \text{ m} \\
&\text{D) } 18 \text{ m} \\
&\text{E) none of other answers}
\end{align*}
\text{Answer C}
\begin{align*}
&\text{A thin hoop rolls without sliding along the floor.} \\
&\text{The ratio of its translational kinetic energy of the center of mass} \\
&\text{to its rotational kinetic energy about an axis through its center of mass is:} \\
\\
&\text{A) } 3 \\
&\text{B) } 2 \\
&\text{C) } 1 \\
&\text{D) } 4 \\
&\text{E) } \frac{1}{2}
\end{align*}
\text{Answer C}
\begin{align*}
&\text{A hoop has a mass of 200 grams and a radius of 25 cm.} \\
&\text{It rolls without slipping along level ground at } 500\,\text{cm/s}. \\
&\text{Its total kinetic energy is:} \\
\\
&\text{A) } 2\,\text{J} \\
&\text{B) } 25\,\text{J} \\
&\text{C) } 10\,\text{J} \\
&\text{D) } 5\,\text{J} \\
&\text{E) } 0\,\text{J}
\end{align*}

\begin{align*}
&\text{A uniform solid sphere of radius } 0.10\,\text{m rolls smoothly across a horizontal table} \\
&\text{at a speed of } 0.50\,\text{m/s} \text{ with total kinetic energy } 0.70\,\text{J}. \\
&\text{Find the mass of the sphere.} \\
\\
&\text{A) } 5.0\,\text{kg} \\
&\text{B) } 8.0\,\text{kg} \\
&\text{C) } 2.0\,\text{kg} \\
&\text{D) } 1.0\,\text{kg} \\
&\text{E) } 4.0\,\text{kg}
\end{align*}
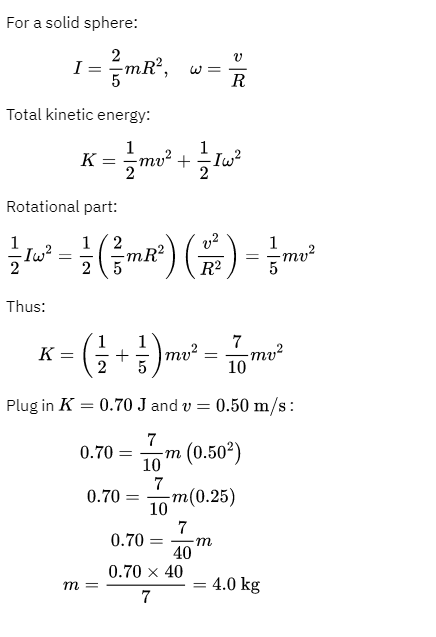
\begin{align*}
&\text{A 3.0 kg wheel, rolling smoothly on a horizontal surface, has a rotational inertia} \\
&\text{about its axis } = \frac{MR^2}{2}, \text{ where } M \text{ is its mass and } R \text{ is its radius.} \\
&\text{A horizontal force is applied to the axle so that the center of mass has an} \\
&\text{acceleration of } 2.0\,\text{m/s}^2. \\
&\text{The magnitude of the frictional force of the surface is:} \\
\\
&\text{A) } 3.0\,\text{N} \\
&\text{B) } 6.0\,\text{N} \\
&\text{C) } 9.0\,\text{N} \\
&\text{D) } 12\,\text{N} \\
&\text{E) } 0\,\text{N}
\end{align*}

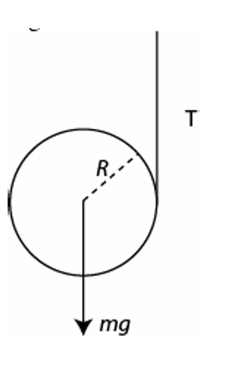
\begin{align*}
&\text{A string is wrapped around a solid disk of mass } m \text{ and radius } R. \\
&\text{The string is vertical and the disk is released from rest.} \\
&\text{Find the tension } T \text{ in the string.}
\end{align*}

\begin{align*}
&\text{What is the net torque about the origin on an object located at } (0,\,-5.0,\;5.0)\,\text{m} \\
&\text{when forces } \vec{F}_1 = (-3.0\,\mathbf{k})\,\text{N} \text{ and } \vec{F}_2 = (2.0\,\mathbf{j})\,\text{N} \text{ act on the object?} \\
\\
&\text{A) } (15\,\mathbf{i})\,\text{N.m} \\
&\text{B) } (5.0\,\mathbf{i})\,\text{N.m} \\
&\text{C) } (10\,\mathbf{j})\,\text{N.m} \\
&\text{D) } (-3.0\,\mathbf{k} + 2.0\,\mathbf{j})\,\text{N.m} \\
&\text{E) Zero}
\end{align*}
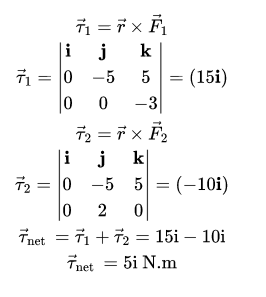
\begin{align*}
&\text{A 2.0 kg particle is moving such that its position vector relative to the origin is} \\
&\quad \mathbf{r} = (-2.0 t^{2}\,\mathbf{i} + 3.0\,\mathbf{j}) \,\text{m}. \\
&\text{What is the torque (about the origin) acting on the particle at } t = 2.0\,\text{s}? \\
\\
&\text{A) } -24\,\mathbf{k}\,\text{N.m} \\
&\text{B) } -36\,\mathbf{k}\,\text{N.m} \\
&\text{C) } 24\,\mathbf{k}\,\text{N.m} \\
&\text{D) } -48\,\mathbf{k}\,\text{N.m} \\
&\text{E) } 0
\end{align*}

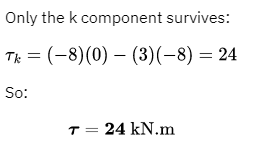
\begin{align*}
&\text{A 2.0 kg stone is tied to a 0.50 m string and swung around a circle} \\
&\text{at a constant angular velocity of } 12\,\text{rad/s}. \\
&\text{The net torque on the stone about the center of the circle is:} \\
\\
&\text{A) } 0 \\
&\text{B) } 6.0\,\text{N.m} \\
&\text{C) } 12\,\text{N.m} \\
&\text{D) } 72\,\text{N.m} \\
&\text{E) } 140\,\text{N.m}
\end{align*}

\begin{align*}
&\text{A particle located at the position vector } \mathbf{r} = (1.2\,\mathbf{i} + 1.2\,\mathbf{j})\,\text{m} \\
&\text{has a force } \mathbf{F} = (150\,\mathbf{i})\,\text{N} \text{ acting on it.} \\
&\text{The torque (in N.m) of the force about the origin is:} \\
\\
&\text{A) } -180\,\mathbf{j} \\
&\text{B) } 180\,\mathbf{k} \\
&\text{C) } 180\,\mathbf{i} \\
&\text{D) } 180(\mathbf{i} + \mathbf{j}) \\
&\text{E) } -180\,\mathbf{k}
\end{align*}
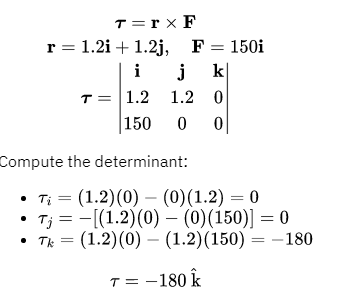
\begin{align*}
&\text{A particle, held by a string whose other end is attached to a fixed point } C, \\
&\text{moves in a circle on a horizontal frictionless surface. If the string is cut,} \\
&\text{the angular momentum of the particle about the point } C: \\
\\
&\text{A) increases} \\
&\text{B) changes direction but not magnitude} \\
&\text{C) does not change} \\
&\text{D) decreases} \\
&\text{E) becomes zero}
\end{align*}
\text{Answer c}
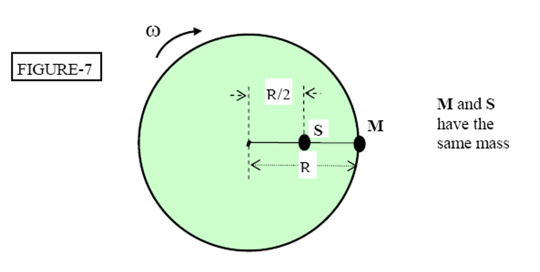
\begin{align*}
&\text{Mohammed (M) and Salim (S) have the same mass and are riding on a merry-go-round} \\
&\text{rotating at a constant rate. Salim is halfway in from the edge. Let the angular} \\
&\text{momenta of Salim and Mohammed about the axis of rotation be } L_s \text{ and } L_m, \text{ respectively.} \\
&\text{Which of the following relations is correct?} \\
\\
&\text{A) } L_m = 2 L_s \\
&\text{B) } L_m = L_s \\
&\text{C) } L_m = \frac{L_s}{4} \\
&\text{D) } L_m = 4 L_s \\
&\text{E) } L_m = \frac{L_s}{2}
\end{align*}
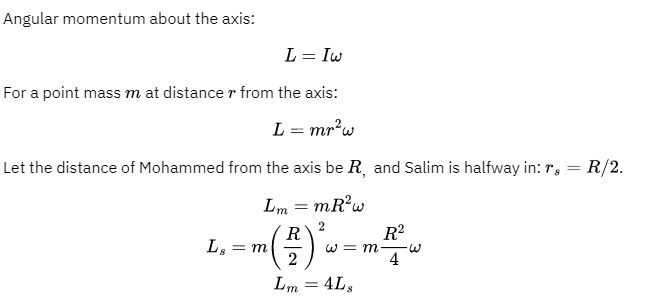
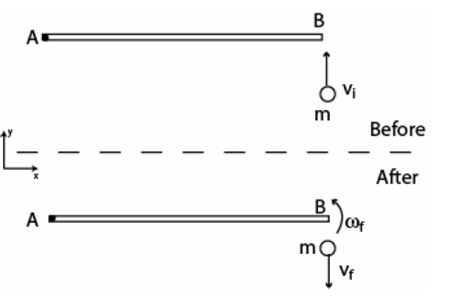
\begin{align*}
&\text{Fig. 7 shows an overhead view of a thin rod of mass } M = 2.0\,\text{kg} \text{ and length } L = 2.0\,\text{m} \\
&\text{which can rotate horizontally about a vertical axis through the end } A. \\
&\text{A particle of mass } m = 2.0\,\text{kg} \text{ traveling horizontally with velocity } \mathbf{v}_i = 10\,\mathbf{j}\,\text{m/s} \\
&\text{strikes the rod at point } B \text{ and rebounds with velocity } \mathbf{v}_f = -6.0\,\mathbf{j}\,\text{m/s}. \\
&\text{Find the angular speed } \omega_f \text{ of the rod just after the collision.} \\
\\
&\text{A) } 24\,\text{rad/s} \\
&\text{B) } 2.0\,\text{rad/s} \\
&\text{C) } 10\,\text{rad/s} \\
&\text{D) } 50\,\text{rad/s} \\
&\text{E) } 30\,\text{rad/s}
\end{align*}
\text{Answer A}
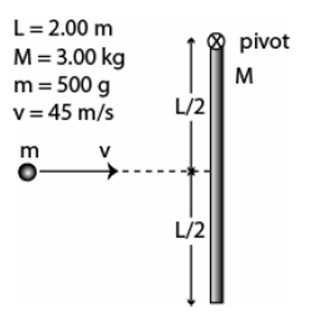
\begin{align*}
&\text{A thin uniform rod of mass } M = 3.0\,\text{kg} \text{ and length } L = 2.0\,\text{m} \\
&\text{is suspended vertically from a frictionless pivot at its upper end.} \\
&\text{An object of mass } m = 0.5\,\text{kg}, \text{ traveling horizontally with speed } v = 45\,\text{m/s}, \\
&\text{strikes the rod at its center of mass and sticks there (see Fig. 6).} \\
&\text{Find the angular velocity of the system just after the collision.} \\
\\
&\text{A) } 0.57\,\text{rad/s} \\
&\text{B) } 2.1\,\text{rad/s} \\
&\text{C) } 4.3\,\text{rad/s} \\
&\text{D) } 3.7\,\text{rad/s} \\
&\text{E) } 5.0\,\text{rad/s}
\end{align*}
\text{Answer E}
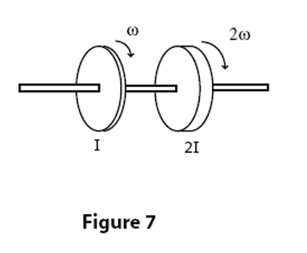
\begin{align*}
&\text{Fig. 7 shows two disks mounted on bearings on a common axis.} \\
&\text{The first disk has rotational inertia } I \text{ and is spinning with angular velocity } \omega. \\
&\text{The second disk has rotational inertia } 2I \text{ and is spinning in the same direction with angular velocity } 2\omega. \\
&\text{The two disks are slowly forced toward each other along the axis until they stick.} \\
&\text{Find the final common angular velocity } \omega_f. \\
\\
&\text{A) } \mathrm{~\omega} \\
&\text{B) } \mathrm{~\omega} \sqrt{3} \\
&\text{C) } \frac{5\mathrm{~\omega}}{3} \\
&\text{D) } 3\mathrm{~\omega} \\
&\text{E) } 2\mathrm{~\omega}
\end{align*}
\text{Answer C}
\begin{align*}
&\text{A man, with his arms at his sides, is spinning on a light turntable} \\
&\text{that can rotate freely about a vertical frictionless axis. When he extends his arms:} \\
\\
&\text{A) his angular momentum will increase} \\
&\text{B) his angular velocity will decrease} \\
&\text{C) his angular velocity remains the same} \\
&\text{D) his rotational inertia decreases} \\
&\text{E) his rotational kinetic energy remains the same}
\end{align*}
\text{Answer B}
\begin{align*}
&\text{A disk with rotational inertia } 2I \text{ rotates with angular velocity } \omega_0 \\
&\text{about a vertical, frictionless axle. A second disk with rotational inertia } I \\
&\text{and initially at rest drops onto the first disk (see Fig. 5). The two disks stick together.} \\
&\text{Find the final angular velocity } \omega \text{ of the system.} \\
\\
&\text{A) } \frac{2}{3} \mathrm{~\omega_0} \\
&\text{B) } \frac{1}{2} \mathrm{~\omega_0}\\
&\text{C) } \frac{3}{4} \mathrm{~\omega_0} \\
&\text{D) } \mathrm{~\omega_0} \\
&\text{E) } 2 \mathrm{~\omega_0}
\end{align*}

\begin{align*}
&\text{A star of radius } R \text{ is spinning with angular velocity } \omega. \\
&\text{If it shrinks so that its radius becomes } R/2, \\
&\text{find the ratio of the final angular momentum to its initial angular momentum.} \\
\\
&\text{A) } 4 \\
&\text{B) } 2 \\
&\text{C) } 1 \\
&\text{D) } 1/2 \\
&\text{E) } 1/4
\end{align*}

Chapter 11-Phys101
By smstry
Chapter 11-Phys101
- 106



