Book 4. Valuation and Risk Models

FRM Part 1

VRM 9. Pricing Conventions, Discounting and Arbitrage

Presented by: Sudhanshu

Module 1. Discount Factors And Arbitrage

Module 2. Bond Components and Pricing

Module 1. Discount Factors And Arbitrage

Topic 1. Fundamentals of Bond Valuation

Topic 2. Calculating the Value of a Coupon Bond

Topic 3. Valuation with Semiannual Discounting

Topic 4. Price-Yield Curve

Topic 5. Discount Factors and Bond Pricing

Topic 6. Discount Factors for Treasury Bills

Topic 7. Discount Factors for Treasury Bonds

Topic 8. Determining Value Using Discount Functions

Topic 1. Fundamentals of Bond Valuation

  • Bond value = Present Value (PV) of all expected future cash flows.

  • Cash flows from a bond:

    • Periodic coupon payments.

    • Repayment of principal at maturity.

  • Steps:
    1. Estimate all future cash flows.
    2. Determine appropriate discount rate.
    3. Calculate PV using:
      • ​​
  • Where
    • CCC = Coupon, FFF = Face Value, rrr = discount rate, NNN = periods.
  • For a Treasury-bond, r= risk-free rate
  • For a non-Treasury bond, a risk premium is added to risk-free rate.
\text { Bond Price }=\sum_{t-1}^N \frac{C}{(1+r)^t}+\frac{F}{(1+r)^N}

Topic 2. Calculating the Value of a Coupon Bond

  • Coupon bonds are valued using the present value of an annuity and lump-sum repayment.
  • Example:
    • Annual coupon = $100
    • Maturity = 10 years
    • Face value = $1,000
    • Discount rate = 8%
  • Compute using:

 

 

 

 

  • This implies a buyer is willing to pay $1,134 today for $100 annual coupons and $1,000 principal in 10 years.
\begin{aligned} &\begin{gathered} P V_{\text {coupon }}=100 \times\left[\frac{1-(1+0.08)^{-10}}{0.08}\right]=671 \\ P V_{\text {principal }}=\frac{1000}{(1+0.08)^{10}}=463 \end{gathered}\\ &\text { Total Bond Value }=671+463=1,134 \end{aligned}

Topic 3.  Valuation with Semiannual Discounting

  • Bonds often pay coupons semiannually. Adjustments:

    • Divide annual coupon and rate by 2.

    • Double the number of periods.

  • Example:

    • $100 annual coupon → $50 every 6 months.

    • 8% annual rate → 4% per 6 months.

    • 10 years → 20 periods.

  • 10 years → 20 periods.

 

 

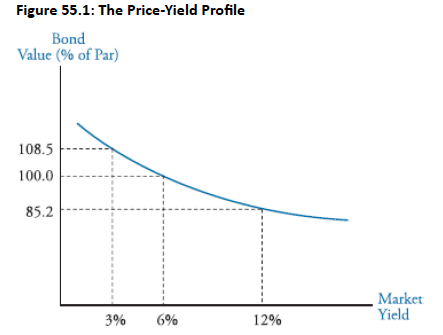
P V=50 \times\left[\frac{1-(1+0.04)^{-20}}{0.04}\right]+\frac{1000}{(1+0.04)^{20}}=1,135.90

Topic 4.  Price-Yield Curve

  • Bond values and yields are inversely related
  • Discount rate increases → Present value of cash flows decreases → Bond price falls
  • Discount rate decreases → Present value of cash flows increases → Bond price rises
  • Price change calculation: Difference between present values at two different discount rates
  • Key characteristic: Higher prices associated with lower yields
  • Shape: Curved (not straight line)
  • For option-free bonds: Convex toward origin (looks like half of a smile)
  • Convexity: Important property affecting bond price sensitivity to yield changes

Topic 5. Discount Factors and Bond Pricing

  • Discount Factor d(n)d(n)d(n): Present value of $1 received n periods in the future.
  • General formula:​

 

  • Present Value of any cash flow:​
  • Example: ​d(0.5)=0.92432
    • ​
d(n)=\frac{1}{(1+r)^n}
P V=\text { Cash Flow } \times d(n)
\$ 100 \text { in } 6 \text { months } \rightarrow 100 \times 0.92432=92.43

Topic 6. Discount Factors for Treasury Bills

  • T-bills are short-term (<1 year) zero-coupon securities.
  • Price formula using quoted price (Q) & no of calendar days until maturity (n) 
    • ​

  • Example:

    • Bid = 99.60, Ask = 99.65 → Mid = 99.625 → DF = 0.99625​

    • Interpretation: A security worth $100,000 in 80 days is worth $99,625 today.

\text { Cash Price }=100-\frac{\mathrm{Qn}}{360}

Topic 7. Discount Factors for Treasury Bonds

  • Securities issued by government to finance their mid- or long-term needs.
  • T-bonds provide periodic coupons and face value at maturity.
  • Use T-bond prices to generate discount function.
  • Example:
    • ​
  • If d(1) = 0.9939, then:
    • ​
  • Using d(2), a T-bond with 2 years of maturity can be priced.
  • Repeat recursively to derive entire discount function.
3.625 \cdot d(1)+103.625 \cdot d(2)=105.98
d(2)=\frac{105.98-(3.625 \cdot 0.9939)}{103.625}=0.9880

Practice Questions: Q1

 

 

 

 

Q1. Which of the following is the closest to the discount factor for the 6-month discount factor, d(0.5)?
A. 0.8923.
B. 0.9304.
C. 0.9525.
D. 0.9863.

\begin{array}{ccc} \hline \text { Maturity } & \text { Coupon } & \text { Price } \\ \hline \text { 6 months } & 5.5 \% & 101.3423 \\ \text { 1 year } & 14.0 \% & 102.1013 \\ \text { 2 years } & 8.5 \% & 99.8740 \\ \hline \end{array}

Practice Questions: Q1 Answer

Explanation: D is correct.

 

 

\begin{aligned} & 101.3423=102.75 \times d(0.5) \\ & d(0.5)=0.9863 \end{aligned}

Practice Questions: Q2

 

 

 

 

Q2. Which of the following is the closest to the discount factor for the 1-year discount factor, d(1)?
A. 0.8897.
B. 0.9394.
C. 0.9525.
D. 0.9746.

\begin{array}{ccc} \hline \text { Maturity } & \text { Coupon } & \text { Price } \\ \hline \text { 6 months } & 5.5 \% & 101.3423 \\ \text { 1 year } & 14.0 \% & 102.1013 \\ \text { 2 years } & 8.5 \% & 99.8740 \\ \hline \end{array}

Practice Questions: Q2 Answer

Explanation: A is correct.

 

 

 

 

\begin{aligned} & 102.1013=[7 \times \mathrm{d}(0.5)]+[107 \times \mathrm{d}(1)] \\ & 102.1013=7(0.9863)+107 \times \mathrm{d}(1) \\ & 95.1972=107 \times \mathrm{d}(1) \\ & \mathrm{d}(1)=0.8897 \end{aligned}

Topic 8. Determining Value Using Discount Functions

  • Law of One Price:

    • Identical future cash flows → Same present value.

    • If violated, leads to arbitrage opportunity.
  • Bond Pricing Using Discount Functions:

 

  • Arbitrage Strategy:

    • Buy undervalued bond.

    • Short overvalued bond with identical cash flows.

    • Profit from price difference with no risk.

  • Example: If 2-year coupon bond is underpriced vs. STRIPS, buy bond, strip it, and sell the components.
\text { Bond Value }=\sum C F_t \cdot d(t)

Module 2. Bond Components and Pricing

Topic 1. STRIPS

Topic 2. Constructing a Replicating Portfolio

Topic 3. Constructing a Replicating Portfolio: Example

Topic 3. Pricing Conventions Between Coupon Dates

Topic 5. Accrued Interest (AI)

Topic 6. Day Count Conventions

Topic 1. STRIPS

  • STRIPS = Separate Trading of Registered Interest and Principal Securities.

  • Treasury bonds split into:

    • P-STRIPS: Principal components.

    • C-STRIPS: Coupon components.

  • No reinvestment risk → pure zero-coupon.
  • Arbitrage when:

​

\text { Price of Bond } \neq \sum \text { (P-STRIPS + C-STRIPS) }

Topic 2. Constructing a Replicating Portfolio

  • Goal: Replicate a bond’s cash flows using other bonds.
  • Steps:
    • Identify bond to replicate.
    • Match cash flows using other available bonds.
    • Solve backward from last payment.
  • If total price of replicating portfolio ≠ target bond → arbitrage exists.

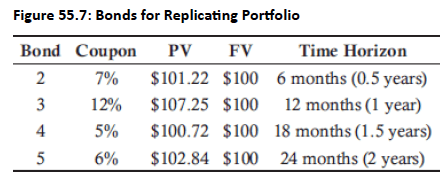
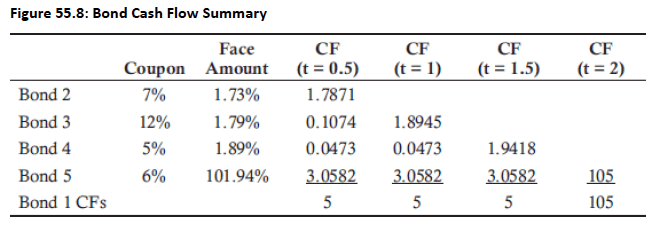
Topic 3. Replicating Portfolio: Example

  • Suppose a 2-year fixed-income security exists with $100 face value and a 10% coupon rate. The coupons are paid on a semiannual basis, and the security’s YTM is assumed to be 4.5%.
    •  
    •  
  • Bond 1 can be replicated using appropriate FV of bond 2, bond 3, bond 3 and bond 4.
    •  
    •  
  • It is easier to start from end:
    • ​
    •  
  • Similarly, we can calculate F3 and F2.
\mathrm{PV}_{\mathrm{B} 1}=\frac{5}{1.0225^1}+\frac{5}{1.0225^2}+\frac{5}{1.0225^3}+\frac{105}{1.0225^4}=\$ 110.41
\text { Bond 1 } \mathrm{CF}_{\mathrm{t}}=\mathrm{F}_2 \times \frac{7 \%}{2}+\mathrm{F}_3 \times \frac{12 \%}{2}+\mathrm{F}_4 \times \frac{5 \%}{2}+\mathrm{F}_5 \times \frac{6 \%}{2}
\text{F5: }\mathrm{FV}_5 \times \frac{100+\frac{6}{2}}{100}=\$ 105; \text{and F4: }\mathrm{FV}_4 \times \frac{100+\frac{5}{2}}{100}+101.94 \times \frac{3}{100}=\$ 5

Topic 4. Pricing Conventions Between Coupon Dates

  • Bonds often trade between coupon dates.
  • Pricing must include interest earned since last coupon.
  • Clean Price = Quoted market price (excludes interest).
  • Dirty Price = Clean Price + Accrued Interest.

 

  • When bond is sold between coupon dates:
    • ​Buyer pays seller for interest accrued up to settlement.
\text { Dirty Price }=\text { Clean Price }+ \text { AI }

Topic 5. Accrued Interest (AI)

  • Interest earned since last coupon:

 

  • Example:
    • ​$1,000 par bond, 10% annual coupon → $50 every 6 months.
    • 90 days elapsed in a 180-day period:

​

  • Buyer pays  this accrued amount to the seller.
\text { Accrued Interest }=\text { Coupon Payment } \times \frac{\text { Days Elapsed }}{\text { Days in Period }}
A I=50 \times \frac{90}{180}=25

Topic 6. Day Count Conventions

  • Used to calculate accrued interest and fractional periods.
  • Common conventions:
    • Actual/Actual: U.S. government bonds.
    • 30/360: U.S. corporates and municipal bonds.
    • Actual/360: Many money markets.
    • Actual/365: Used in Canada, New Zealand and Australia.
  • Example:
    • Semiannual coupon bond, 30/360 → 180 days per period.

 

  • Impacts:
    • Accrued interest.
    • Pricing between coupon dates.
  • Adjusts the denominator in the accrued interest formula based on standard day assumptions.
\text { Fraction }=\frac{\text { Days Since Last Coupon }}{180}

Practice Questions: Q3

Q3. Which of the following day count conventions would most likely be used in pricing an Australian money market security?
A. 30/360.
B. Actual/360.
C. Actual/365.
D. Actual/actual.

Practice Questions: Q3 Answer

Explanation: C is correct.

The actual/365 day count convention is typically used for money market securities in Canada, New Zealand, and Australia.

Practice Questions: Q4

Q4. A EUR 100,000 par value French corporate bond pays 3.5% coupon with a semiannual frequency. Assume the last coupon was paid 75 days ago and there are 30 days in each month. The accrued interest is closest to:
A. 729.
B. 1,094.
C. 1,458.
D. 2,917.

Practice Questions: Q2 Answer

Explanation: A is correct.

 

 

 

\begin{aligned} & 100,000 \times 3.5 \% / 2=1,750 \\ & 1,750 \times \frac{75}{180}=\text { EUR } 729.17 \end{aligned}

Copy of VRM 9. Pricing Conventions, Discounting and Arbitrage

By Prateek Yadav

Copy of VRM 9. Pricing Conventions, Discounting and Arbitrage

  • 25

More from Prateek Yadav

  • MR 13. Expectations, Risk Premium, Convexity, and the Shape of the Term Structure
    Prateek Yadav
    0
  • MR 11. Regression Hedging and Principal Component Analysis
    Prateek Yadav
    5
  • MR 10. Financial Correlation Modeling-Bottom up Approaches
    Prateek Yadav
    1