Book 4. Valuation and Risk Models

FRM Part 1

VRM 12. Applying Duration, Convexity and DV01

Presented by: Sudhanshu

Module 1. Dollar Value of a Basis Point

Module 2. Duration and Convexity

Module 1. Dollar value of a Basis point

Topic 1. One-factor Interest Rate Model

Topic 2. DV01 Of a Fixed Income Security

Topic 3. DV01 Application to Hedging

Topic 1. One-factor Interest Rate Model

Interest rate factors are random variables that influence individual interest rates along the yield curve.
A one-factor model assumes that all interest rate movements can be explained by a single source of randomness.
This single factor often represents the overall level of interest rates (e.g., the short-term rate).
Limitation: The most limiting assumption of portfolio duration is that rate changes are assumed to be parallel across the yield curve. This may not hold true in reality.
Examples:
- If the 2-year spot rate increases by 3 basis points, all other spot rates are assumed to increase by 3 basis points.
- Interest rates could move in the same direction, but not in a parallel way. For example, short-term interest rates could increase more than long-term rates.

Topic 2. DV01 of a Fixed Income Security

DV01 (Dollar Value of a 01): The dollar value change in a fixed-income security’s price for a one basis point (0.01%) change in interest rates.
Formula:
Types of DV01:
- Yield-based DV01: Changes in bond prices from changes in YTM.
- DVDZ or DPDZ: Changes in bond prices from changes in spot rates.
- DVDF or DPDF: Changes in bond prices from changes in forward rates.

DV01=-\Delta P/\Delta y

\Delta P = \text{Change in Portfolio Value}

\Delta Y = \text{Size of a Parallel Shift in Interest Rate Term Structure}

Practice Questions: Q1

Q1. An investor has a short position valued at $100 in a 10-year, 5% coupon bond with a 7% yield to maturity (YTM). Assume discounting occurs on a semiannual basis.
Which of the following is closest to the dollar value of a basis point (DV01)?

A. 0.033.

B. 0.047.

C. 0.056.

D. 0.065.

Practice Questions: Q1 Answer

Explanation: D is correct.

For a 7.01% bond,

For a 6.99% bond,

N = 20; I/Y = 7.01 / 2 = 3.505\%; PMT = 2.5; FV = 100; CPT → PV = –85.723

N = 20; I/Y = 6.99 / 2 = 3.495\%; PMT = 2.5; FV = 100; CPT → PV = –85.852

DV01 = |85.852 – 85.723| / 2 = 0.0645

Topic 3. DV01 Application to Hedging

Goal of Hedging:
- To produce a combined investment + hedge position that will not change in value for a small change in yield.
Hedge Ratio (HR) Calculation (Bond with another bond):
Applying the Hedge Ratio:
- The calculated HR is multiplied by the face value of the initial position to arrive at the face value of the hedging instrument required.

HR=\frac{\text{DV01 (Initial Position)}}{\text{DV01 (Hedging Instrument)}}

\text {Face Value of Hedging Instrument }=\text {Face Value of Initial Position } \times \mathrm{HR}

Practice Questions: Q2

Q2. An investor has a short position valued at $100 in a 10-year, 5% coupon bond with a 7% yield to maturity (YTM). Assume discounting occurs on a semiannual basis.

Using a 20-year T-bond with a DV01 of 0.085 to hedge the interest rate risk in the 10-year bond with a DV01 of 0.065, which of the following actions should the investor take?

A. Buy $76.50 of the hedging instrument.

B. Sell $76.50 of the hedging instrument.

C. Buy $130.75 of the hedging instrument.

D. Sell $130.75 of the hedging instrument.

Practice Questions: Q2 Answer

Explanation: A is correct.

The HR is 0.065/0.085 = 0.765. Since the investor has a short position in the bond, this means the investor needs to buy $0.765 of par value of the hedging instrument for every $1 of par value for the 10-year bond.

Module 2. Duration And Convexity

Topic 1. Duration

Topic 2. Callable and Putable Bonds

Topic 3. DV01 Vs Duration

Topic 4. Convexity

Topic 5. Price Change Using Both Duration and Convexity

Topic 6. Portfolio Duration and Portfolio Convexity

Topic 7. Hedging Example

Topic 8. Barbell and Bullet Portfolios

Topic 9. Barbell and Bullet Portfolios: Example

Topic 1. Duration

Duration:
- Duration is the most widely used measure of bond price volatility.
- A bond’s price volatility is a function of its coupon, maturity, and initial yield.
- Duration captures the impact of all three of these variables in a single measure.
Effective Duration:
- Measures the percentage change in a security’s value for a particular unit’s change in rates.
- It can be interpreted as the percentage change in a bond’s price for a 100 basis point change in rates.
- Formula:
From above formula, bond pricing can be approximated as:
- $Δ P$ = Change in bond price, $D$ = Duration, $P$ = Initial bond price, $Δ y$ = Change in yield

\Delta P \approx -D \times P \times \Delta y

D=-\frac{\Delta P / P}{\Delta y}=-\frac{\Delta P}{P \Delta y}

Callable Bonds:
- Calculation Approaches for Duration:
  1. Assume the bond would not be called in the future.
  2. Calculate duration as the weighted probability that the bond would not be called and the probability that it would be called.
  3. More Precise Approach: Calculate duration by valuing the bond’s price today, revaluing the price for an assumed 1 basis point parallel change in interest rates, and calculating duration from the percentage change in the bond’s price.
Putable Bonds:
- The effective duration of a putable bond is calculated similarly to callable bonds.

Topic 2. Callable and Putable Bonds

\mathrm{D}=P_{\text{called}}\left(\mathrm{D}_{\text {called }}\right)+P_{\text{non-called}}\left(\mathrm{D}_{\text {not called }}\right)

Topic 3. DV01 Vs Duration

DV01 measures the change in dollar value of a security for every basis point change in rates, duration measures the percentage change in a security’s value for a unit change in rates.
Duration is more convenient for traditional investors who are interested in the percentage change in price and overall interest rate sensitivity.
DV01 is more suitable for hedgers who are interested in the absolute dollar change in price for a small interest rate movement.

Topic 4. Convexity

Definition:
- Convexity is the sensitivity of duration to changes in interest rates.
- It measures the curvature of the bond price-yield relationship.
Characteristics:
- Convexity is generally positive for standard bonds.
- Positive convexity will always increase the price calculated by duration only (meaning it's beneficial for investors).
Calculation:
- Where:
  - $P$ = Initial bond price
  - $P_{+}$ = Price after a small increase in yield
  - $P_{-}$ = Price after a small decrease in yield
  - $Δ y$ = Small change in yield

C=\frac{1}{P} \times \left[\frac{P_{+}+P_{-}-2P}{(\Delta y)^{2}}\right]

Topic 5. Price Change Using Both Duration and Convexity

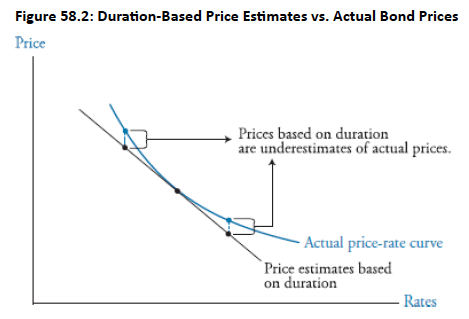
Convexity is important and why estimates of price changes based solely on duration alone are inaccurate.
Combining Duration and Convexity:
- Provides a more accurate estimate of bond price changes, especially for larger interest rate movements.
Combined Effect Calculation:

\Delta P \approx -D \times P \times \Delta y+\frac{1}{2} \times C \times P \times (\Delta y)^{2}

Practice Questions: Q3

Q3. What is the estimate for the percentage price change in bond price from a 25 basis point increase in rates on a bond with a duration of 7 and a convexity of 243?

A. 1.67% decrease.

B. 1.67% increase.

C. 1.75% increase.

D. 1.75% decrease.

Practice Questions: Q3 Answer

Explanation: A is correct.

\begin{aligned} \Delta \mathrm{P} & =[-7 \times 0.0025 \times \mathrm{P}]+\left[\frac{1}{2} \times 243 \times(0.0025)^2\right] \times \mathrm{P} \\ & =-1.67 \% \times \mathrm{P}, \text { or a decrease of } 1.67 \% \end{aligned}

Topic 6. Portfolio Duration and Portfolio Convexity

Portfolio Duration:
- If rate changes are parallel, the duration of a portfolio of individual securities equals the value-weighted sum of the individual durations.
- Where:
  - $D_{i}$ = Duration of bond $i$
  - $w_{i}$ = Market value of bond $i$ / Market value of portfolio
  - $K$ = Number of bonds in portfolio
Portfolio Convexity:
- Similar to portfolio duration, convexity for the entire portfolio is simply the value-weighted average of each individual security’s convexity within the portfolio.

\text{Duration of Portfolio}=\sum_{i=1}^{K} w_{i} \times D_{i}

Practice Questions: Q4

Q4. The duration of a portfolio can be computed as the sum of the value-weighted durations of the bonds in the portfolio. Which of the following is the most limiting assumption of this approach?

A. All weights must be different.

B. The portfolio must be equally weighted.

C. The rate changes are assumed to be parallel.

D. All the bonds in the portfolio must be in the same risk class or along the same yield curve.

Practice Questions: Q4 Answer

Explanation: C is correct.

Duration measures assume a parallel shift in the yield curve. Duration is not a good measure of nonparallel shifts.

Topic 7. Hedging Example

Hedging with One Bond (Duration Only):
- To fully hedge an investment with value $V$ and duration $D_{V}$ using a bond with value $P$ and duration $D_{P}$ :
For a full hedge ( $Δ V = Δ P$ ):

Hedging with Two Bonds (Duration and Convexity):
- An investor can hedge using two bonds with prices $P_{1}$ , $P_{2}$ , durations $D_{1}$ , $D_{2}$ , and convexities $C_{1}$ , $C_{2}$ .
- The conditions for a duration and convexity hedge are:
  1. (Matching durations)
  2. (Matching convexities)

\begin{aligned} & \Delta V=-D_V \times V \times \Delta y \\ & \Delta P=-D_P \times P \times \Delta y \end{aligned}

V \times D_V=P \times D_P \Longrightarrow P=\frac{V \times D_V}{D_P}

D _{V} ×V−P_{ 1} ×D_{ 1} −P _{ 2} ×D _{ 2} =0

C _{V} ×V−P_{ 1} ×C_{ 1} −P _{ 2} ×C_{ 2} =0

Topic 8. Barbell and Bullet Portfolios

Barbell Strategy:
- An investment manager uses bonds with short and long maturities, thus forgoing any intermediate-term bonds.
- Benefit: Typically has higher convexity than a bullet portfolio of the same duration.
- Performance:
  - Outperforms in parallel increases in interest rates due to higher convexity.
  - Often underperforms in nonparallel changes in interest rates.
Bullet Strategy: An investment manager buys a single bond, typically concentrated in the intermediate maturity range.
Arbitrage Opportunities: Arbitrageurs might exploit differences in expected performance between bullet and barbell strategies based on anticipated interest rate changes.
For example, if the manager believes that rates will be especially volatile, the barbell portfolio would be preferred over the bullet portfolio.

Topic 9. Barbell and Bullet Portfolios: Example

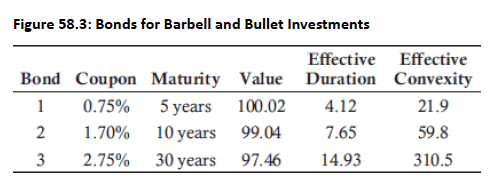
Assume that an investor is looking to construct a $100,000 portfolio with a duration of 7.65.
Bullet Portfolio: The investor could buy $100,000 of the 10-year bond (Bond 2) with a duration of 7.65.
Barbell Portfolio: The investor could construct a portfolio using a shorter and longer maturity bond (using the 5-year and 30-year bonds) with a weighted duration of 7.65. Assume weight in 5-year bond to be
- Therefore, the investor could construct a portfolio with a duration of 7.65 by investing 67.35% of funds in the 5-year Bond 1 and investing (1 – 67.35%) = 32.65% in the 30-year Bond 3.
- The barbell portfolio's convexity is:
- A higher convexity is beneficial because it improves the investor’s position for parallel changes in interest rates.

w_1.

4.12 w_1+14.93\left(1-w_1\right)=7.65 \implies w_1=0.6735

0.6735 \times 21.9+0.3265 \times 310.5=116.1

Copy of VRM 12. Applying Duration, Convexity and DV01

By Prateek Yadav

Copy of VRM 12. Applying Duration, Convexity and DV01

Book 4. Valuation and Risk Models

FRM Part 1

VRM 12. Applying Duration, Convexity and DV01

Presented by: Sudhanshu

Module 1. Dollar Value of a Basis Point

Module 2. Duration and Convexity

Module 1. Dollar value of a Basis point

Topic 1. One-factor Interest Rate Model

Topic 2. DV01 of a Fixed Income Security

Practice Questions: Q1

Practice Questions: Q1 Answer

Topic 3. DV01 Application to Hedging

Practice Questions: Q2

Practice Questions: Q2 Answer

Module 2. Duration And Convexity

Topic 1. Duration

Topic 2. Callable and Putable Bonds

Topic 3. DV01 Vs Duration

Topic 4. Convexity

Topic 5. Price Change Using Both Duration and Convexity

Practice Questions: Q3

Practice Questions: Q3 Answer

Topic 6. Portfolio Duration and Portfolio Convexity

Practice Questions: Q4

Practice Questions: Q4 Answer

Topic 7. Hedging Example

Topic 8. Barbell and Bullet Portfolios

Topic 9. Barbell and Bullet Portfolios: Example

Copy of VRM 12. Applying Duration, Convexity and DV01

More from Prateek Yadav