Book 1. Market Risk

FRM Part 2

MR 9. Empirical Properties of Correlation

Presented by: Sudhanshu

Module 1.  Empirical Properties of Correlation

Module 1.  Empirical Properties of Correlation

Topic 1. Correlations During Different Economic States

Topic 2. Mean Reversion

Topic 3. Autocorrelation

Topic 4. Best-Fit Distributions for Correlations

Topic 5. Johnson SB Distributions

Topic 6. Generalized Extreme Value (GEV) Distribution

Topic 1. Correlations During Different Economic States

• Findings:Empirical Study (1972–2017):
  • Analyzed 30 Dow stocks each month (480,600 correlations over 534 months).
  • Formed 30×30 correlation matrices.
• Economic State Classification (based on GDP):
  • Expansionary: GDP > 3.5%
  • Normal: GDP between 0% and 3.5%
  • Recession: Two consecutive quarters of negative GDP
• Findings:
  • Average Correlation Levels:
    • Recession: 37.0%
    • Normal: 33.0%
    • Expansion: 27.5%

• Findings:
  • Correlation Volatility:
    • Recession: 80.5%
    • Normal: 83.0% (Highest)
    • Expansion: 71.2%
• ​Interpretation:
  • Correlations rise during recessions due to systemic market moves.
  • Volatility is surprisingly highest in normal periods due to market uncertainty.
  • Expansion periods reflect more idiosyncratic stock behavior.
• Key takeaway: Risk managers must model higher correlations and volatility during recessions.

Practice Questions: Q1

Q1. Suppose a risk manager examines the correlations and correlation volatility of stocks in the Dow Jones Industrial Average (Dow) for the period beginning in 1972 and ending in 2017. Expansionary periods are defined as periods where the U.S. gross domestic product (GDP) growth rate is greater than 3.5%, periods are normal when the GDP growth rates are between 0 and 3.5%, and recessions are periods with two consecutive negative GDP growth rates. Which of the following statements characterizes correlation and correlation volatilities for this sample? The risk manager will most likely find that:
A. correlations and correlation volatility are highest for recessions.
B. correlations and correlation volatility are highest for expansionary periods.
C. correlations are highest for normal periods, and correlation volatility is highest for recessions.
D. correlations are highest for recessions, and correlation volatility is highest for normal periods.

Practice Questions: Q1 Answer

Explanation:  D is correct.

Findings of an empirical study of monthly correlations of Dow stocks from 1972 to 2017 revealed the highest correlation levels for recessions and the highest correlation volatilities for normal periods. The correlation volatilities during a recession and normal period were 80.5% and 83.0%, respectively.

Topic 2.  Mean Reversion 

Definition:

Tendency for a variable to revert to its long-term average over time.

Equation:

•      value at time $t$,
•     long-term mean,
•   : mean reversion rate

Example:

• If
  • $a=0.5$ → Expected change = 15
  • $a=1.0$ → Expected change = 30

• Estimation using Regression:
  • Reformulated as:
    •  
    •  
    •  
• Empirical Result (1972–2017):
  • Regression:

Conclusion:

Equity correlations exhibit high mean reversion – a sharp pullback toward mean after deviation.

Topic 3. Autocorrelation

• Definition:

Measures persistence in a variable; how much current values depend on past values.

• Opposite of Mean Reversion:

• If mean reversion = 78%, autocorrelation = 22%
• Formula:

• Findings from Study:
  • 1-month lag autocorrelation: ~21%
  • 2-month lag (highest): ~26%
  • Decay: Down to ~10% by 10-month lag
• Interpretation:
  • Correlations in financial time series are not persistent long-term.
  • Supports modeling via mean-reverting processes.

Topic 4.  Best-Fit Distributions for Correlations

• Goal: Identify statistical distributions that best fit historical correlation data for equities, bonds, and defaults.
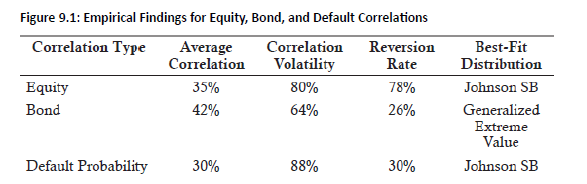
• Equity Correlations:
  • Best Fit: Johnson SB distribution
    • ​Flexible: 2 shape + 1 location + 1 scale parameter
    • Superior to normal, lognormal, and beta
  • Empirical Result: 77% of equity correlations were positive.
• Bond Correlations:
  • Average Correlation: 42%
  • Volatility: 64%
  • Mean Reversion Rate: 26%
  • Best Fit: Generalized Extreme Value (GEV)
    • ​Normal distribution also acceptable.

• Default Correlations:
  • Average: 30%,
  • Volatility: 88%,
  • Mean Reversion Rate: 30%
  • Best Fit: Johnson SB, like equities

Topic 5.  Johnson SB Distribution

• Definition:
  • A flexible distribution suited for bounded variables.
  • Defined by:
    • 2 shape parameters,
    • 1 location parameter,
    • 1 scale parameter
• Why it fits well:
  • Accurately captures asymmetry and bounded behavior of correlation data (which must lie between –1 and +1).
  • Handles fat tails and skewed distributions better than normal/lognormal.
• Empirical Support:
  • Best fit for:
    • Equity correlation distributions (Dow 1972–2017)
    • Default probability correlation distributions
  • ​Outperformed:​
    • Normal, lognormal, and beta distributions

Topic 6. Generalized Extreme Value (GEV) Distribution

• Definition:
  • A family of distributions used to model extreme outcomes, such as maxima or minima.
  • Includes three types: Gumbel, Frechét, Weibull (depending on shape parameter).
• Why it fits bond correlations:
  • Captures tail risk and extreme co-movements in bond markets.
  • Bond correlations exhibit less volatility than equity but still show fat-tail behavior.
• Empirical Support:

  • Best fit for:

    • Bond correlation distributions (7,645 bond correlations studied)
  • Normal distribution also acceptable, but less accurate in tail behavior.

• Key Statistics:
  • Bond Correlation Mean: 42%
  • Volatility: 64%
  • Mean Reversion Rate: 26%

Practice Questions: Q2

Q2. Suppose mean reversion exists for a variable with a value of 30 at time period t − 1. Assume that the long-run mean value for this variable is 40 and ignore the stochastic term included in most regressions of financial data. What is the expected change in value of the variable for the next period if the mean reversion rate is 0.4?
A. −10.
B. −4.
C. 4.
D. 10.

Practice Questions: Q2 Answer

Explanation:  C is correct.

The mean reversion rate,    , indicates the speed of the change or reversion back to the mean. If the mean reversion rate is 0.4 and the difference between the last variable and long-run mean is 10 (= 40 − 30), the expected change for the next period is 4 (i.e., 0.4 × 10 = 4).

Practice Questions: Q3

Q3. A risk manager uses the past 480 months of correlation data from the Dow Jones Industrial Average (Dow) to estimate the long-run mean correlation of common stocks and the mean reversion rate. Based on historical data, the long-run mean correlation of Dow stocks was 32%, and the regression output estimates the following regression relationship: Y = 0.24 − 0.75X. Suppose that in April 2014, the average monthly correlation for all Dow stocks was 36%. What is the expected correlation for May 2014 assuming the mean reversion rate estimated in the regression
analysis?
A. 32%.
B. 33%.
C. 35%.
D. 37%.

Practice Questions: Q3 Answer

Explanation:  B is correct.

There is a −4% difference from the long-run mean correlation and April 2014 correlation (32% − 36% = −4%). The inverse of the β coefficient in the regression relationship implies a mean reversion rate of 75%. Thus, the expected correlation for May 2014 is 33.0%:

Practice Questions: Q4

Q4. A risk manager uses the past 480 months of correlation data from the Dow Jones Industrial Average (Dow) to estimate the long-run mean correlation of common stocks and the mean reversion rate. Based on this historical data, the long-run mean correlation of Dow stocks was 34%, and the regression output estimates the following regression relationship: Y = 0.262 − 0.77X.
Suppose that in April 2014, the average monthly correlation for all Dow stocks was 33%. What is the estimated one-period autocorrelation for this time period based on the mean reversion rate
estimated in the regression analysis?
A. 23%.
B. 26%.
C. 30%.
D. 33%.

Practice Questions: Q4 Answer

Explanation:  A is correct.

The autocorrelation for a one-period lag is 23% for the same sample. The sum of the mean reversion rate (77% given the beta coefficient of −0.77) and the one period autocorrelation rate will always equal 100%.

Practice Questions: Q5

Q5. In estimating correlation matrices, risk managers often assume an underlying distribution for the correlations. Which of the following statements most accurately describes the best-fit distributions for equity correlation distributions, bond correlation distributions, and default probability correlation distributions? The best-fit distribution for the equity, bond, and default probability
correlation distributions, respectively, are:
A. lognormal, generalized extreme value, and normal.
B. Johnson SB, generalized extreme value, and Johnson SB.
C. beta, normal, and beta.
D. Johnson SB, normal, and beta.

Practice Questions: Q5 Answer

Explanation: B is correct.

Equity correlation distributions and default probability correlation distributions are best fit with the Johnson SB distribution. Bond correlation distributions are best fit with the generalized extreme value distribution.