Book 1. Market Risk

FRM Part 2

MR 2. Non-Parametric Approaches

Presented by: Sudhanshu

Module 1. Nonparametric Approaches

Module 1. Nonparametric Approaches

Topic 1. Introduction to Nonparametric Approaches

Topic 2. Bootstrap Historical Simulation & Limitations of Traditional Methods

Topic 3.  Nonparametric Density Estimation (NDE)

Topic 4.  Weighted Historical Simulation – Overview

Topic 5.  Age-Weighted Historical Simulation

Topic 6.  Volatility-Weighted Historical Simulation

Topic 7. Correlation-Weighted Historical Simulation

Topic 8. Filtered Historical Simulation (FHS)

Topic 9. Advantages and Disadvantages of Nonparametric Methods

Topic 1. Introduction to Nonparametric Approaches

• Definition: Nonparametric estimation does not assume a fixed form for the distribution (unlike normal/lognormal in parametric models).
• Approach: Fully data-driven. Suitable for modeling tail risks where assumptions like normality break down.
• Main Use: Value at Risk (VaR) estimation and Expected Shortfall (ES) under flexible assumptions.
• Key Point: Smoother and more adaptable than traditional methods.

Topic 2. Bootstrap Historical Simulation & Limitations of Traditional Methods

• Traditional Historical Simulation: Limitations
  • VaR is computed from sorted historical returns.
  • With $n$ observations, VaR can only be calculated at n discrete confidence levels (e.g., 95%, 96%, ..., 99%).
  • Example: With 100 observations, 95.5% VaR cannot be computed.
  • Leads to coarse estimations and poor resolution for confidence levels between two points.
• ​Bootstrap Historical Simulation: A Better Approach
  • Resampling technique to enhance estimation accuracy and flexibility.
  • Process:
    • Draw random samples (with replacement) from the historical dataset.
    • Compute VaR or ES for each sample.
    • Repeat this process $B$ times.
    • Final estimate = Average of all computed risk measures.

• Equation for VaR using Bootstrapping:

• Equation for Expected Shortfall (ES):
  • Slice the tail of each sample into $n$ slices and average the VaRs at each of the $n-1$ quantiles.
• ​Benefits Over Traditional Simulation:
  • Resolves the discreteness issue—better resolution at any confidence level.

  • Improves estimation precision by accounting for data variability.

  • Can be easily extended to compute Expected Shortfall as well.

Practice Questions: Q1

Q1. Johanna Roberto has collected a data set of 1,000 daily observations on equity returns. She is
concerned about the appropriateness of using parametric techniques as the data appears skewed.
Ultimately, she decides to use historical simulation and bootstrapping to estimate the 5% VaR.
Which of the following steps is most likely to be part of the estimation procedure?
A. Filter the data to remove the obvious outliers.
B. Repeated sampling with replacement.
C. Identify the tail region from reordering the original data.
D. Apply a weighting procedure to reduce the impact of older data.

Practice Questions: Q1 Answer

Explanation:  B is correct.

Bootstrapping from historical simulation involves repeated sampling with replacement. The 5% VaR is recorded from each sample draw. The average of the VaRs from all the draws is the VaR estimate. The bootstrapping procedure does not involve filtering the data or weighting observations. Note that the VaR from the original data set is not used in the analysis.

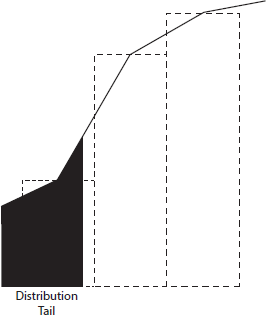
Topic 3. Nonparametric Density Estimation (NDE)

Solution to discreteness problem

• Key Idea: Smooth the histogram to allow continuous VaR estimation.
• Method: Connect the midpoints between bars (histogram columns).
• Outcome: Create a continuous, surrogate density function.
• Shows area redistribution between bars.
• Shaded area = Confidence interval (e.g., VaR at 95.5%).
• Advantage: Enables VaR at any confidence level.
• Advanced methods: Use curves (e.g., kernel smoothing) instead of straight lines for higher accuracy.

Topic 4. Weighted Historical Simulation – Overview

• Traditional historical simulation assigns equal weights to all $n$ observations.
• Observations beyond the cutoff get zero weight.
• Problems:
  • No differentiation between recent and old data.
  • Ghost effects: Past extreme events may affect current risk estimates unnecessarily.

Practice Questions: Q2

Q2. All of the following approaches improve the traditional historical simulation approach for estimating VaR except the:
A. volatility-weighted historical simulation.
B. age-weighted historical simulation.
C. market-weighted historical simulation.

D. correlation-weighted historical simulation.

Practice Questions: Q2 Answer

Explanation:  C is correct.

Market-weighted historical simulation is not discussed in this reading. Ageweighted historical simulation weights observations higher when they appear closer to the event date. Volatility-weighted historical simulation adjusts for changing volatility levels in the data. Correlation-weighted historical simulation incorporates anticipated changes in correlation between assets in the portfolio.

Topic 5. Age-Weighted Historical Simulation

• Proposed by Boudoukh, Richardson, Whitelaw (1998).

• Assign exponentially decaying weights to past data:

  • More recent data → higher weight.

  • Older data → lower weight.

• Equation:

Where:

• $\lambda \in [0,1]$ is the decay parameter.
• $i$ is the age of the observation (1 = most recent).
• If $\lambda =1$, → equal weights (traditional historical simulation).
• If $\lambda \to 0$, → only the most recent data matters.

Advantage: Smoothly fades out old events, reducing ghost effects.

Topic 6.  Volatility-Weighted Historical Simulation

• Developed by Hull and White (1998).
• Weigh observations by adjusting them for current vs historical volatility.
• Volatility-adjusted return formula:

Where:

•            original return on day $i$
•          volatility on day $i$
•          current volatility estimate
• Current risk is better captured if recent volatility ≠ historical volatility.
• Model used for σ: GARCH or EWMA.

​Pros:

• Adapts to changing volatility.

• Allows for estimation of losses larger than historical losses.

Topic 7. Correlation-Weighted Historical Simulation

• ​​Extends volatility-weighted method by adjusting for correlation.
• Updates variance-covariance matrix:
  • Diagonal: variances of individual assets.
  • Off-diagonal: covariances between asset pairs.
• Instead of raw returns:

• No manual calculation needed for FRM exam—just conceptual understanding.

Advantage: Captures co-movement of assets more effectively in dynamic markets.

Practice Questions: Q3

Q3. Which of the following statements about age-weighting is most accurate?
A. The age-weighting procedure incorporates estimates from GARCH models.
B. If the decay factor in the model is close to 1, there is persistence within the data set.
C. When using this approach, the weight assigned on day i is equal to

D. The number of observations should at least exceed 250.

Practice Questions: Q3 Answer

Explanation: B is correct.

If the intensity parameter (i.e., decay factor) is close to 1, there will be persistence (i.e., slow decay) in the estimate. The expression for the weight on day i has i in the exponent when it should be n. While a large sample size is generally preferred, some of the data may no longer be representative in a large sample.

Topic 8. Treasury Bond Futures Price

• Combines:
  • Bootstrapping
  • Historical Simulation
  • Volatility modeling (GARCH or asymmetric GARCH)

Steps:

• Forecast daily volatility using GARCH.
• Standardize historical returns:

• Bootstrap standardized returns.
• Multiply bootstrapped returns by current volatility to get simulated returns.
• Compute VaR from simulated data.

​Pros:

• Captures volatility clustering and asymmetry.
• More robust for tail risk estimation.
• Efficient for large portfolios.

Topic 9. Advantages and Disadvantages of Nonparametric Methods

Advantages:

• Flexible and easy to implement (Excel-friendly)
• No distributional assumptions (works with skewed/fat-tailed data)
• Avoids complex matrix calculations
• Can be enhanced (e.g., combine age-weighted + volatility-weighted)

Disadvantages:

• Dependent on historical data:
  • Doesn’t predict what hasn’t happened.
• Doesn’t adapt well to:
  • Regime shifts
  • Market structure changes
• May under- or over-estimate risk:
  • Quiet periods → underestimation
  • Volatile periods → overestimation

Practice Questions: Q4

Q4. Which of the following statements about volatility-weighting is true?
A. Historic returns are adjusted, and the VaR calculation is more complicated.
B. Historic returns are adjusted, and the VaR calculation procedure is the same.
C. Current period returns are adjusted, and the VaR calculation is more complicated.
D. Current period returns are adjusted, and the VaR calculation is the same.

Practice Questions: Q4 Answer

Explanation: B is correct.

The volatility-weighting method adjusts historic returns for current volatility. Specifically, return at time t is multiplied by (current volatility estimate / volatility estimate at time t). However, the actual procedure for calculating VaR using a historical simulation method is unchanged; it is only the inputted data that changes.

Topic 2. Limitations of Duration

• Duration assumes:

  • Linear price/yield relationship

  • Parallel shifts in yield curve

• Limitations:

  • Inaccuracy for large changes in rates

  • Cannot handle non-parallel yield curve shifts

  • Ignores convexity of bond pricing

Practice Questions: Q5

Q5. All of the following items are generally considered advantages of nonparametric estimation methods except:
A. ability to accommodate skewed data.
B. availability of data.
C. use of historical data.
D. little or no reliance on covariance matrices.

Practice Questions: Q5 Answer

Explanation: C is correct.

The use of historical data in nonparametric analysis is a disadvantage, not an
advantage. If the estimation period was quiet (volatile) then the estimated risk measures may understate (overstate) the current risk level. Generally, the largest VaR cannot exceed the largest loss in the historical period. On the other hand, the remaining choices are all considered advantages of nonparametric methods. For instance, the nonparametric nature of the analysis can accommodate skewed data, data points are readily available, and there is no requirement for estimates of covariance matrices.