Book 4. Valuation and Risk Models

FRM Part 1

VRM 16. Option Sensitivity Measures- The Greeks

Presented by: Sudhanshu

Module 1. Naked and Covered Positions

Module 2. Delta and Delta Hedging

Module 3. Theta, Gamma, Vega and Rho

Module 1. Naked And Covered Positions

Topic 1. Risks in Naked and Covered Option Positions

Topic 2. Stop-Loss Strategy

Topic 1. Risks in Naked and Covered Option Positions

  • Naked Call Position: Occurs when a party sells a call option without owning the underlying asset.

    • Potential Loss: Unlimited, as the stock price can rise without bound.
    • Maximum Gain: Capped at the premium received.
    • Example: Selling 10,000 call options at a $23 strike price for a $4 premium on a stock trading at $20. Revenue is $40,000. If the stock expires at $30, the loss is $70,000, resulting in a net loss of $30,000.

  • Covered Call Position: Occurs when the party selling a call option owns the underlying asset.

    • Risk Mitigation: Minimizes the cost of short options by locking in revenue from the option sale, as the firm already owns the shares if the option is exercised.
    • Potential Loss: If the stock price falls significantly, the loss on the long stock position can be substantially larger than the premium received.
    • Example: Owning 10,000 shares and selling call options. If the stock falls to $10, the long stock position decreases by $100,000, which is greater than the option premium.

Practice Questions: Q1

Q1. An investor takes a short position in a call option on ABC stock with a current price of $15 and a strike price of $18. If the investor does not own the underlying stock, the biggest risk to the investor is:

A. a loss on the premium paid.

B. the stock price rising above $18.

C. the stock price falling below $15.

D. a decline in the overall stock market.

Practice Questions: Q1 Answer

Explanation: B is correct. Selling a call without the underlying stock to support it is called a naked call position, and the investor who sells the call is therefore vulnerable to the underlying stock increasing above the strike price. The higher the price goes above the strike price, the more likely it is that the call will be exercised and the investor will then have to go out into the market and buy the stock (at now higher prices) to cover the call. The seller of the option receives the premium, so there will not be a loss on the premium paid for the seller.

Topic 2. Stop-Loss Strategy

  • Purpose: Designed to limit losses associated with short option positions (call writers).
  • Mechanism:
    • Requires purchasing the underlying asset for a naked call position when the asset rises above the option's strike price.
    • The asset is then sold when it falls below the strike price.
    • Objective: To maintain a naked position when the option is out of the money and a covered position when it is in the money.
  • Advantages: Tends to work well when an option is initially in the money.
  • Disadvantages:
    • Transaction Costs: Can become high due to frequent buying and selling of the asset if the stock price fluctuates around the exercise price.
    • Price Uncertainty: Uncertainty about whether the asset will be above or below the strike price at expiration.

Practice Questions: Q2

Q1. Stop-loss strategies with call options require purchasing the underlying asset for a:

A. naked call position when the asset falls below the option’s strike price.

B. naked call position when the asset rises above the option’s strike price.

C. covered call position when the asset falls below the option’s strike price.

D. covered call position when the asset rises above the option’s strike price.

Practice Questions: Q2 Answer

Explanation: B is correct. Stop-loss strategies with call options are designed to limit the losses associated with short option positions. The strategy requires purchasing the underlying asset for a naked call position when the asset rises above the option’s strike price.

Module 2. Delta And Delta Hedging

Topic 1. Option Delta

Topic 2. Forward Delta and Futures Delta

Topic 3. Dynamic Aspects of Delta Hedging

Topic 4. Maintaining the Hedge

Topic 5. Other Portfolio Hedging Approaches

Topic 1. Option Delta

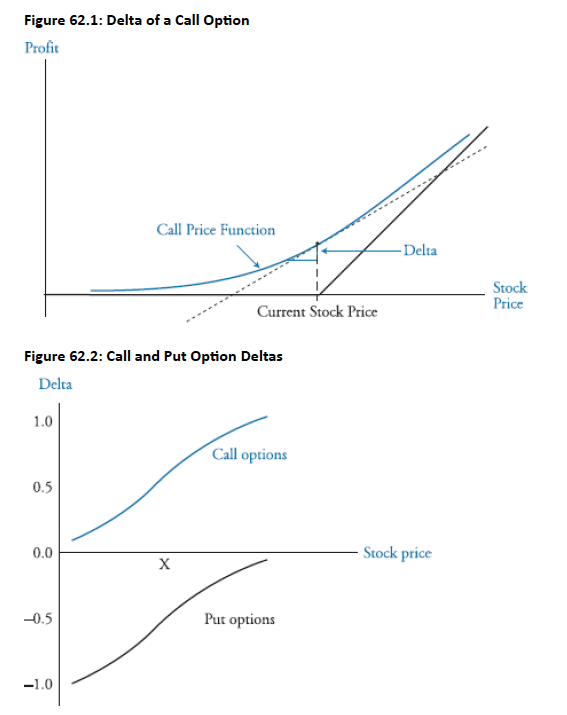
  • Definition: The ratio of the change in price of an option to the change in price of the underlying asset, for small changes in the underlying asset's price.
  • Formula (for a call option): ​ 
    •     = change in the call option price
    •     = change in the stock price
  • Interpretation: Represents the slope of the call option pricing function at the current stock price.
  • Range of Values:
    • Call option deltas range from 0 to +1.
    • Put option deltas range from -1 to 0.
  • Example: A call delta of 0.60 means the call option price will change by approximately $0.60 for a $1.00 change in the stock value.
  • Delta-Neutral Hedging: To completely hedge a long stock or short call position, an investor must purchase (or short) the number of shares of stock equal to delta times the number of options sold. This creates a delta-neutral position.
    • For a short 1,000 call options with a delta of 0.6, the investor needs to be long 600 (0.6 x 1,000) shares of the underlying.
  • Black-Scholes-Merton Model: Delta can also be calculated as the N(d1) in the Black-Scholes-Merton option pricing model.
\Delta=\partial c/\partial s
\partial c
\partial s

Topic 1. Option Delta

Practice Questions: Q3

Q3. Which of the following choices will effecively hedge a short call option position that exhibits a delta of 0.5?

A. Sell two shares of the underlying for each option sold.

B. Buy two shares of the underlying for each option sold.

C. Sell the number of shares of the underlying equal to half the options sold.

D. Buy the number of shares of the underlying equal to half the options sold.

Practice Questions: Q3 Answer

Explanation: D is correct.

To hedge a short call option position, a manager would have to buy enough of the underlying to equal the delta times the number of options sold. In this case, delta = 0.5, so for every two options sold, the manager would have to buy a share of the underlying security.

  • Forward Delta:

    • The delta of a forward position is equal to one.
    • Implies a one-to-one relationship between the value of the forward contract and its underlying asset.
    • Easily hedged with an offsetting underlying asset position with the same number of securities.
    • Adjusted for Dividends (q): If a dividend yield exists, the delta of a forward contract is         

  • Futures Delta:

    • Generally not one due to the spot-futures parity relationship.
    • For non-dividend-paying stock/index: Delta is         , where r is the risk-free rate and T is time to maturity.
    • For assets with dividend yield (q): Delta is              
    • Short futures positions are hedged by going long the deliverable asset.

Topic 2. Forward Delta and Future Delta

e^{- qT}.
e^{rT}
e^{(r- q) T}.

Practice Questions: Q4

Q4. If the risk-free rate is 3% and the time to maturity is nine months, the delta of a forward position is closest to:

A. 0.98.

B. 1.00.

C. 1.02.

D. 2.25.

Practice Questions: Q4 Answer

Explanation: B is correct.

This question does not require any calculations, as the relationship between a forward and the underlying asset is one to one, making the delta equal to exactly 1.00.

Topic 3. Dynamic Aspects of Delta Hedging

  • Delta as a Function of Stock Price: The delta of an option changes as the underlying stock price changes.
  • Rebalancing: When delta changes, the portfolio is no longer hedged, requiring the investor to buy or sell the underlying asset continually to maintain a delta-neutral position.
  • Goal of Delta-Neutral Portfolio: To combine an asset position with an option position such that the portfolio's value remains unchanged by fluctuations in the asset's value.
  • Creating a Delta-Neutral Portfolio: For a stock position, a risk-free combination can be a long stock position and a short call position, where the number of calls to short is given by

​ 

 

  • Example: An investor owning 60,000 shares of ABC stock  with a call option (strike $50, delta 0.60) needs to short 100,000 call options to create a delta-neutral hedge.  ​
1/ \Delta_C .
\left(60,000/0.6 = 100,000\right)
\text { Number of options needed }=\frac{\text { number of shares hedged }}{\text { delta of call option }}

Topic 4. Maintaining the Hedge

  • Limited Effectiveness of Delta-Neutral Position: A delta-neutral position only holds for very small changes in the underlying stock's value.
  • Frequent Rebalancing (Dynamic Hedging): The delta-neutral portfolio must be frequently or continuously rebalanced to maintain the hedge because the option's delta changes as the underlying stock price changes.
  • Costly Process: Continuously maintaining a delta-neutral position can be very costly due to transaction costs from closing out options or selling additional contracts.
  • Dynamic vs. Static Hedging:
    • Dynamic Hedging: Adjusting the hedge on a frequent basis.
    • Static Hedging (Hedge-and-Forget): Setting up the hedge initially and never adjusting it.
  • Example of Rebalancing: If the stock price moves from 50 to $51, and the call option delta changes from 0.60 to 0.62, the investor needs to adjust the number of short call options. If they initially shorted 100,000 options for 60,000 shares, they now need to short 96,774 options (                                    ), meaning 32 option contracts would need to be purchased.
60,000/0.62 \approx 96,774

Practice Questions: Q5

Q5. A static hedging strategy will be least effective when the underlying stock price:

A. increases from $4 to $6.

B. increases from $20 to $21.

C. decreases from $26 to $25.

D. decreases from $35 to $34.

Practice Questions: Q5 Answer

Explanation: A is correct.

An increase in the underlying stock price from $4 to $6 is not only the largest dollar change of the choices given, but also it is the largest percentage change. Static hedging (the hedge-and-forget strategy) is only effective when there are small changes in the stock price. To protect against larger changes, dynamic hedging needs to be deployed.

Topic 5. Other Portfolio Hedging Approaches

  • A delta-neutral hedge can be achieved by buying enough put options to offset the gain or loss on the underlying asset.
  • Relationship: Value of puts = -Δ value of long stock position.
  • Number of Puts: Purchase [1/ (call delta - 1)] put options to protect each long share of stock.
  • Rebalancing: Just as important as with calls.
  • Example (using puts): For 60,000 shares of ABC stock (long) and a call option with delta 0.60, the put option delta is (0.60 - 1) = -0.40. To hedge, the investor needs to purchase 150,000 put options:

 

(-60,000)/(-0.4)=150,000

Module 3. Theta, Gamma, Vega, And Rho

Topic 1. Theta

Topic 2. Gamma

Topic 3. Relationship Between Delta, Theta, and Gamma

Topic 4. Vega

Topic 5.Rho

Topic 6. Delta, Gamma, and Vega Of a Portfolio

Topic 7. Hedging Activities in Practice

Topic 8. Portfolio Insurance

Topic 1. Theta

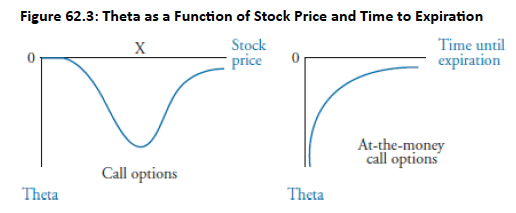
  • Definition: Measures an option's sensitivity to a decrease in time to expiration; also known as time decay. For a call option,
  • Variation: Theta varies with changes in stock prices and as time passes.
  • Black-Scholes-Merton Formula for European Calls (non-dividend-paying):  
    • ​
  • Characteristics:
    • Generally affects put and call options similarly (most decrease in value as time passes).
    • Most pronounced when the option is at-the-money, especially nearer to expiration.
    • Usually negative, indicating option value decreases closer to expiration.
    • Increases in absolute value as expiration approaches.
    • Possible for in-the-money European put options to have positive theta.
\Theta=\partial c/\partial t
\Theta(call)=-\frac{S_0 N^{\prime}\left(d_1\right) \sigma}{2 \sqrt{T}}-r X e^{-r T} N\left(d_2\right);
\Theta(put)=-\frac{S_0 N^{\prime}\left(d_1\right) \sigma}{2 \sqrt{T}}+r X e^{-r T} N\left(-d_2\right)
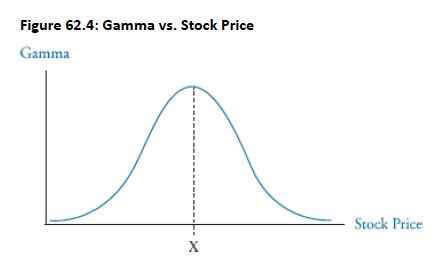
  • Definition: Represents the expected change in the delta of an option. It measures the curvature of the option price function not captured by delta. For a call option,  
  • Calculation (for European call or put options on non-dividend-paying stocks): ​​
  • Interpretation: For a $1 change in stock price, delta will change by the gamma value.
  • Relationship with Stock Price: Gamma is largest when an option is at-the-money. Deep in-the-money or out-of-the-money options have little sensitivity to gamma.
  • Hedging:
    • When gamma is large, delta changes rapidly; when small, delta changes slowly.
    • Delta-neutral positions hedge against small stock price changes, while gamma helps hedge against large changes.
    • It is desirable to create both delta-neutral and gamma-neutral positions to protect against both small and large stock price changes.

Topic 2. Gamma

\Gamma=\partial^2 c/\partial s^2
\Gamma=N' (d_1)/S_0 \sigma \sqrt{T}

Practice Questions: Q6

Q6. A delta-neutral position exhibits a gamma of –3,200. An existing option with a delta equal to 0.5 exhibits a gamma of 1.5. Which of the following will generate a gamma-neutral position for the existing portfolio? 

A. Buy 2,133 of the available options.

B. Sell 2,133 of the available options.

C. Buy 4,800 of the available options.

D. Sell 4,800 of the available options.

Practice Questions: Q6 Answer

Explanation: A is correct.

To create a gamma-neutral position, a manager must add the appropriate number of options that equals the existing portfolio gamma position. In this case, the existing gamma position is –3,200, and an available option exhibits a gamma of 1.5, which translates into buying approximately 2,133 options (= 3,200 /1.5).

Practice Questions: Q7

Q7. Which of the following actions would have to be taken to restore a delta-neutral hedge to the gamma-neutral position?

A. Buy 1,067 shares of the underlying stock.

B. Sell 1,067 shares of the underlying stock.

C. Buy 4,266 shares of the underlying stock.

D. Sell 4,266 shares of the underlying stock

Practice Questions: Q7Answer

Explanation: B is correct.

The gamma-neutral hedge requires the purchase of 2,133 options, which will then increase the delta of the portfolio to 1,067 (= 2,133 × 0.5). Therefore, this would require selling approximately 1,067 shares to maintain a delta-neutral position.

Practice Questions: Q8

Q8. An option with a strike price of $12 and a current stock price of $12 that has one week until expiration is likely to have a gamma to an option seller that is:

A. positive and large.

B. positive and small.

C. negative and large.

D. negative and small.

Practice Questions: Q8 Answer

Explanation: C is correct.

Gamma is the most negative for at-the-money options near expiration for an option seller. An option with a strike price and current price of $12 will be at the money.

Topic 3. Relationship Between Delta, Theta, and Gamma

  • Stock option prices are directly affected by their sensitivities to Delta, Theta, and Gamma.
    • ​
  • For a delta-neutral portfolio (Δ = 0), so
    • ​
  • The left side of the equation is the dollar risk-free return on the option.

  • Assuming the risk-free rate is small, this demonstrates that for large positive values of theta, gamma tends to be large and negative, and vice versa, which explains the common practice of using theta as a proxy for gamma.

r \Pi=\Theta+r S \Delta+0.5 \sigma^2 S^2 \Gamma
r \Pi=\Theta+r S \Delta+0.5 \sigma^2 S^2 \Gamma
r \Pi=\Theta+0.5 \sigma^2 S^2 \Gamma
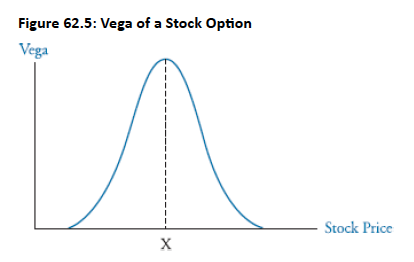
  • Definition: Measures the sensitivity of an option's price to changes in the volatility of the underlying stock. For a call option:
    • ​
  • It can be noted that vega is not a Greek letter).
  • Interpretation: A vega of 8 indicates that for a 1% increase in volatility, the option's price will increase by 0.08.
  • For a given maturity, exercise price, and risk-free rate, the vega of a call is equal to the vega of a put.
  • Options are most sensitive to volatility changes when they are at-the-money. Deep out-of-the-money or deep in-the-money options have little sensitivity to volatility (vega is close to zero).
  • Vega for European calls and puts on non-dividend-paying stocks is calculated as:
    • ​

Topic 4. Vega

vega =\partial c/\partial \sigma
vega =S_0 N^{\prime}\left(d_1\right) \sqrt{T}
  • Definition: Measures an option's sensitivity to changes in the risk-free rate.
    • ​
  • Equity Options: Equity options are less sensitive to interest rate changes compared to other variables like volatility and stock price. Large rate changes have only small effects on equity option prices.
  • Importance: Rho is a much more important risk factor for fixed-income derivatives.
  • Sensitivity to Rates: In-the-money calls and puts are more sensitive to rate changes than out-of-the-money options.
    • Increased rates lead to larger increases for in-the-money call prices and larger decreases for in-the-money put prices.
  • For European options on a non-dividend-paying stock, rho is measured as:
    • ​
    •  

Topic 5. Rho

rho =\partial c/\partial r
\operatorname{rho}( call )=\mathrm{XTe}^{-\mathrm{rT}} \mathrm{N}\left(\mathrm{d}_2\right)
\operatorname{rho}( call )=\mathrm{-XTe}^{-\mathrm{rT}} \mathrm{N}\left(\mathrm{-d}_2\right)

Practice Questions: Q9

Q9. Which of the following statements about the Greeks is true?

A. Rho for fixed-income options is small.

B. Call option deltas range from –1 to +1.

C. A vega of 10 suggests that for a 1% increase in volatility, the option price will increase by 0.10.

D. Theta is the most negative for out-of-the-money options.

Practice Questions: Q9 Answer

Explanation: C is correct.

Theta is the most negative for at-the-money options. Call option deltas range from 0 to 1. A vega of 10 suggests that for a 1% increase in volatility, the option price will increase by 0.10. Rho for equity options is small.

  • Portfolio Delta: Calculated as the weighted average delta of each option position in the portfolio. It represents the expected change in the overall option portfolio value for a small change in the underlying asset's price.
    • ​
    •  
  • Portfolio Vega and Gamma: Also computed as the weighted sum of the corresponding vega and gamma positions of the individual options in the portfolio.

Topic 6. Delta, Gamma, and Vega of a Portfolio

\text{Portfolio Delta} =\Delta_p=\sum_{i=1}^n w_i \Delta_i

Practice Questions: Q10

Q10. A portfolio consists of three options. Option 1 has a weighting of 20% and a delta of 0.75, Option 2 has a weighting of 35% and a delta of 0.45, and Option 3 has a weighting of 45% and a delta of 0.60. The portfolio delta is closest to:

A. 0.27.

B. 0.58.

C. 0.60.

D. 1.80.

Practice Questions: Q10 Answer

Explanation: B is correct.

The portfolio delta is a weighted average of the individual option deltas, calculated as follows: (0.20)(0.75) + (0.35)(0.45) + (0.45)(0.60) = 0.58.  

  • Expense of Maintaining Greek-Neutral Positions: A significant challenge for options traders is the cost of trying to maintain positions that are neutral to all "Greeks."
  • Difficulty with Gamma and Vega: While delta-neutral positions are achievable, it's harder to find securities at reasonable prices that can mitigate the negative effects of gamma and vega.
  • Trading Limits: Traders face limits on Greek exposures (e.g., delta limits, gamma limits, vega limits).
  • Common Practice for Financial Institutions: Large financial institutions typically adjust to a delta-neutral position and then monitor their exposure to other Greeks.
  • Offsetting Situations: Institutions selling options often have negative gamma and vega, which worsen over time if the option stays near the money.
    • However, when options are initially sold at the money, their sensitivity to gamma and vega is highest. As time passes, options tend to move in or out of the money, reducing the impact of gamma and vega on the delta-neutral position.
  • Additional Greeks: Traders may also calculate charm (delta sensitivity over time), vanna (delta sensitivity to volatility), and vomma (vega sensitivity to implied volatility change).

Topic 7. Hedging Activities in Practice

  • Definition: The combination of an underlying instrument and either cash or a derivative that establishes a floor value for the portfolio if market values decline, while still allowing for upside potential.
  • Comparison with Delta Hedging: Delta hedging involves combining an initial investment with an opposite position (e.g., hedging a short call with a long underlying stock position). Portfolio insurance involves hedging a long position or portfolio using long put options (or synthetic put options).
  • Implementation:
    • Buying Put Options: The simplest method is to buy put options on the underlying portfolio. Losses on the portfolio can be offset by gains on the long put position.
    • Synthetic Put Position: If direct put options are unavailable or impractical, a synthetic put position can be created using index futures contracts. This involves selling index futures contracts in an amount equivalent to the proportion dictated by the required put option's delta.
  • Advantages of Synthetic Creation with Futures: Substantially lower trading costs and relatively higher levels of liquidity.

Topic 8. Portfolio Insurance

Practice Questions: Q11

Q11. Portfolio insurance payoffs would not involve which of the following?

A. Selling call options in the proportion 1/delta.

B. Buying put options one to one relative to the underlying.

C. Buying and selling the underlying in the proportion of delta of a put.

D. Buying and selling futures in the proportion of delta of a put.

Practice Questions: Q11 Answer

Explanation: A is correct.

Portfolio insurance can be created by all of the statements except selling call options in the proportion 1/delta. This action generates a delta-neutral hedge, not portfolio insurance.