Book 4. Valuation and Risk Models

FRM Part 1

VRM 11. Bond Yields and Returns Calculations

Presented by: Sudhanshu

Module 1. Realized Returns And Bond Spreads

Module 2. Yield To Maturity

Module 3. Bond Return Decomposition

Module 1. Realized Returns And Bond Spreads

Topic 1. Gross and Net Realized Returns

Topic 2. Spread of a Bond

Topic 1. Gross and Net Realized Returns

A bond's realized return compares its ending investment value with its beginning value, incorporating any coupon payments or coupon reinvestment.
The gross realized return (or simply gross return) of a bond is calculated as its end-of-period total value minus its beginning-of-period value, divided by its beginning-of-period value, without factoring in financing costs. The end-of-period total value includes both the ending bond price and any coupons paid during the period.
The formula for realized return from time period $t - 1$ to $t$ is:
Net Realized Return: The net realized return (or simply net return) of a bond is its gross realized return minus per-period financing costs.
Financing costs arise from borrowing cash to purchase the bond.
Reinvestment Risk: Reinvestment risk is the possibility that an investor will earn less when reinvesting the cash flows from an investment than they were previously earning. This can happen when interest rates fall during an investor's investment horizon.

(R_{t-1,t})

R_{t-1,t}=\frac{BV_{t}+C_{t}-BV_{t-1}}{BV_{t-1}}

Practice Questions: Q1

Q1. Reinvestment risk would not occur if:

A. interest rates shifted over the time period the bond is held.

B. the bonds were callable.

C. bonds are issued at par.

D. only zero-coupon bonds are purchased.

Practice Questions: Q1 Answer

Explanation: D is correct.

Callable bonds have reinvestment risk because the principal can be prematurely retired. The higher the coupon, the higher the reinvestment risk, holding all else constant. A bond being issued at par has nothing to do with reinvestment risk.

Topic 2. Spread of a Bond

The market price of a bond may differ from its computed price using spot or forward rates.
This difference is known as the bond spread.
An investor might want to know the spread necessary to add to Treasury forward rates to make the present value of bond cash flows equal the bond price.
The spread (s) can be added to the forward rates (or discount factors) to equate discounted cash flows to the market price:

Deriving this spread helps identify whether the bond is trading cheap or rich in terms of its return.
Spreads generally increase with maturity.

\begin{aligned}\text { Bond Value }&=\frac{\text { Coupon }}{(1+0-12-\text { month forward rate }+s)}\\ &+\frac{(\text { coupon }+ \text { principal })}{[(1+0-12-\text { month forward rate }+s) \times(1+12-24-\text { month forward rate }+s)]}\end{aligned}

Module 2. Yield to Maturity

Topic 1. Yield to maturity (YTM) and Bond’s Pricing

Topic 2. Annuity and Perpetuity
Topic 3. Spot Rates and YTM
Topic 4. Relationship Between YTM, Coupon Rate, and Price
Topic 5. Japanese Yields

Topic 1. Yield to maturity (YTM) and Bond’s Pricing

Definition and Interpretation of YTM: The Yield to Maturity (YTM) of a fixed-income security is equivalent to its internal rate of return.
YTM is the single discount rate that equates the present value of all cash flows from the instrument to its price.
Relationship between YTM, Coupon Rate, and Price:
- If YTM < Coupon Rate, the bond trades at a premium.
- If YTM > Coupon Rate, the bond trades at a discount.
- If YTM = Coupon Rate, the bond trades at par.
Calculation of YTM: For a security with known annual cash flows, the YTM (y) is found by solving:

$P$ = price of the security
= annual cash flow in year k
$N$ = term to maturity in years
$y$ = annual yield or YTM

P=\frac{C_1}{(1+y)^1}+\frac{C_2}{(1+y)^2}+\frac{C_3}{(1+y)^3}+\ldots+\frac{C_N}{(1+y)^N}

C_k

Periodic Yield and YTM (Non-Annual Cash Flows): If cash flows occur more frequently than annually, the equation becomes:

$n = N \times m$ = number of periods (years multiplied by payments per year)
= periodic cash flow in time period k
$y$ = periodic yield or periodic interest rate
Reinvestment Risk and YTM: Reinvestment risk is a significant threat to a bond's computed YTM because YTM calculations assume that coupon cash flows are reinvested at a rate equal to the computed yield. If the average reinvestment rate is below the YTM, the realized yield will also be below the YTM.

P=\frac{C_1}{(1+y)^1}+\frac{C_2}{(1+y)^2}+\frac{C_3}{(1+y)^3}+\ldots+\frac{C_n}{(1+y)^n}

C_k

Topic 1. Yield to maturity (YTM) and Bond’s Pricing

Practice Questions: Q2

Q2. A $1,000 par bond carries a coupon rate of 10%, pays coupons semiannually, and has 13 years remaining to maturity. Market rates are currently 9.25%. The price of the bond is closest to:

A. $586.60.

B. $1,036.03.

C. $1,055.41.

D. $1,056.05.

Practice Questions: Q2 Answer

Explanation: D is correct.

N=26; PMT=50; I/Y=4.625; FV=1000; CPT->PV=\$1056.05

Topic 2. Annuity and Perpetuity

Annuity: An annuity is a series of equal payments made at regular intervals over a specified period of time.
The price (present value) of cash flows (annuities) can be calculated given the YTM (y) and cash flows (C).
Price of a Perpetuity: The perpetuity formula is straightforward:

where:
- $C$ = cash flow that will occur every period into perpetuity
- $y$ = yield to maturity

\text{PV of an Annuity}=\frac{[1-(1+y)^{-n}])}{y}

\text{PV of a perpetuity}=\frac{C}{y}

Practice Questions: Q3

Q3. An annuity pays $10 every year for 100 years and currently costs $100. The YTM is closest to:

A. 5%.

B. 7%.

C. 9%.

D. 10%

Practice Questions: Q3 Answer

Explanation: D is correct.

N=100; PMT=10; PV=-100; CPT-> I/Y =10\%

Practice Questions: Q4

Q4. An investment pays $50 annually into perpetuity and yields 6%. Which of the following is closest to the price?

A. $120.

B. $300.

C. $530.

D. $830.

Practice Questions: Q4 Answer

Explanation: D is correct.

PV=C/I=\$50/0.06=\$833.33

Topic 3. Spot Rates and YTM

The relationship between spot rates and YTM is complex.
With larger coupons, earlier spot rates become more significant in determining the YTM.
Upward Sloping Term Structure: If the term structure of interest rates is upward sloping, earlier spot rates are lower than the spot rate for the final payment date because the largest cash flow occurs at maturity. In this scenario, the YTM declines as the coupon rate increases.
Flat Spot Curve: If the spot curve is flat, the spot rate for early payments is the same as for the final maturity.
Downward Sloping Term Structure: If the term structure of interest rates is downward sloping, the YTM increases as the coupon rate increases.

Topic 4. Relationship Between YTM, Coupon Rate, and Price

Coupon Effect: The coupon effect describes a scenario where two bonds with identical maturities but different coupons will have different yields to maturity.
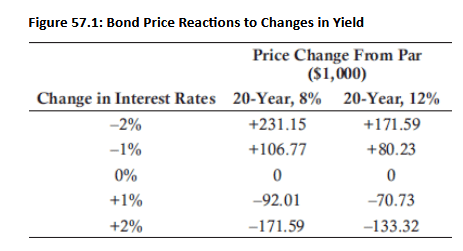
A bond with a smaller coupon will be more sensitive to interest rate changes if all other factors are identical. This means that for any given change in yield, the smaller-coupon bond will experience a larger percentage change in price than the larger-coupon bond.
Interest Rate Risk:
- Lower coupon rate implies greater interest rate risk.
- Higher coupon rate implies lower interest rate risk.

Practice Questions: Q5

Q5. A $1,000 par bond carries a 7.75% semiannual coupon rate. Prevailing market rates are 8.25%. What is the price of the bond?

A. Less than $1,000.

B. $1,000.

C. Greater than $1,000.

D. Not enough information to determine.

Practice Questions: Q5 Answer

Explanation: A is correct.

Because the coupon rate is less than the market interest rate, the bond is a discount bond and trades less than par.

Topic 5. Japanese Yields

Japanese bond yields are typically quoted on a simple yield basis, without factoring in compounding, differing from the U.S. yield convention.
The simple yield is calculated as:

where:

$c$ = coupon
$p$ = principal
$T$ = maturity

\text{yield}=\frac{c}{p}+\frac{(100-p)}{pT}

Module 3. Bond Return Decomposition

Topic 1. Decomposition of the Profit and Loss (P&L) for a Bond Position or Portfolio

Topic 2.Carry Roll-Down Scenarios

Topic 1. Decomposition of the Profit and Loss (P&L) for a Bond Position or Portfolio

Return decomposition for a bond breaks down bond profit and loss (P&L) into component parts. This helps investors understand the sources of their bond investment gains or losses.
The change in a bond's price can be broken down into three component parts for price effect analysis:
1. Carry Roll-Down: The estimated return from bond price movements and coupon payments, assuming no change to interest rate expectations (i.e., expected forward rates are realized and become spot rates). This component does not account for spread changes.
2. Rate Change: The realized return when this realized return differs from what was assumed under the carry roll-down. This component also does not account for spread changes.
3. Spread Change: Accounts for price changes due to changes in the bond's spread relative to other bonds.

Extensions to P&L Analysis:
- Impact of Financing: If financing is considered, the cost of financing should be added as a fourth component of the P&L, and both gross and net returns should be calculated.
- Accrued Interest: If initial and final bond valuations occur between coupon dates, it is necessary to add a fourth component for the impact of accrued interest.

Topic 1. Decomposition of the Profit and Loss (P&L) for a Bond Position or Portfolio

Topic 2. Carry Roll-Down Scenarios

Carry roll-down is the estimated return from bond price movements and coupon payments, assuming no change to interest rate expectations.
Traders often consider "no-change scenarios" for interest rates when making investment return calculations. These include realized forward, unchanged term structure, and unchanged yields.
Realized Forward Scenario:
- This scenario assumes that forward rates for future periods remain unchanged as time passes.
- As forward rates are realized, they become equal to the expected future spot rates.
- When the beginning of a forward period is reached, the forward rate becomes the spot rate.

Unchanged Term Structure Scenario
- This scenario assumes the term structure will remain unchanged over the investment horizon.
- The gross realized return will largely depend on the relationship between the bond's coupon rate and the last forward rate before maturity.
- This implies a risk premium built into forward rates. For example, an upward-sloping term structure that remains unchanged implies an increasing investor risk premium over the investment horizon.
Unchanged Yields Scenario
- This scenario assumes that bond yields remain unchanged over the investment horizon.
- The 1-period gross realized return will equal a bond's yield (i.e., its YTM).
- This scenario assumes that bond coupon payments are reinvested at the YTM. This assumption has limitations because the term structure is unlikely to be flat and remain unchanged.

Topic 2. Carry Roll-Down Scenarios

Practice Questions: Q6

Q6. Assume the 1-year spot rate is 4%, the 1-year forward rate starting in 1 year is 5%, and the 1-year forward rate starting in 2 years is 6%. Under the realized forward scenario, the realized 1-year rate in 1 year would be:

A. 4%.

B. 4.5%.

C. 5%.

D. 5.5%.

Practice Questions: Q6 Answer

Explanation: C is correct.

Under the realized forward scenario, as forward rates are realized, they will be equal to the expected future spot rates. As a result, the realized 1-year rate in 1 year would be 5%.