Book 2. Quantitative Analysis

FRM Part 1

QA 7. Linear Regression

Presented by: Sudhanshu

Module 1. Regression Analysis

Module 2. Ordinary Least Squares Estimation

Module 3. Hypothesis Testing

Module 1. Regression Analysis

Topic 1. Examples of Linear Models

Topic 2. Linear Regression Conditions

Topic 1. Examples of Linear Models

Regression: Measures how changes in a dependent (explained) variable can be explained by changes in one or more independent (explanatory) variables.
Linear relationship: The relationship between variables is captured by estimating a linear equation that quantifies these dependencies.
General Form:
- Where:
  - $E (Y)$ is the expected value of the dependent (or explained) variable.
  - $α$ is the intercept.
  - $β$ is the slope coefficient.
  - $X$ is the independent (or explanatory) variable.
Including the Error Term:
- $ϵ$ (epsilon) represents the random error or shock, which is the unexplained component of Y.
Example: Hedge Fund Returns and Lockup Periods
- $E (re t u r n) = α + β \times (l oc k u p p er i o d)$
Interpretation of $α$ and $β$ :
- $β$ : Regression or slope coefficient; sensitivity of Y to changes in X.
- $α$ : Value of Y when X = 0. If X cannot realistically be 0, $α$ ensures the mean of Y lies on the fitted line.

E(Y)=\alpha+\beta \times (X)

Y=\alpha+\beta \times (X)+\epsilon

Practice Questions: Q1

Q1. Generally, if the value of the independent variable is zero, then the expected value of the dependent variable would be equal to the:

A. slope coefficient.

B. intercept coefficient.

C. error term.

D. residual.

Practice Questions: Q1 Answer

Explanation: B is correct.

The regression equation can be written as: E(Y) = α + β × X. If X = 0, then Y = α
(i.e., the intercept coeficient).

Practice Questions: Q2

Q2. The error term represents the portion of the:

A. dependent variable that is not explained by the independent variable(s) but could possibly be explained by adding additional independent variables.

B. dependent variable that is explained by the independent variable(s).

C. independent variables that are explained by the dependent variable.

D. dependent variable that is explained by the error in the independent variable(s).

Practice Questions: Q2 Answer

Explanation: A is correct.

The error term represents effects from independent variables not included in the model. It could be explained by additional independent variables.

Topic 2. Linear Regression Conditions

To effectively use linear regression, three key conditions must be satisfied:
1. Linear Relationship: The relationship between the dependent variable (Y) and independent variable(s) (X) should be linear.
  - Note: Nonlinear relationships can be made amenable to linear models through appropriate transformations of independent variables (e.g., using $ln (X)$ instead of $X$ ).
2. Additive Error Term: The error term must be additive, meaning its variance is independent of the observed data.
3. Observable X Variables: All independent variables (X) should be observable. Missing data makes the model inappropriate.
Linearity in Coefficients: The dependent variable must be a linear function of the unknown parameters (coefficients). For example, is not linear in coefficients if 'p' is an unknown parameter.

Y=\alpha+\beta X^p +\epsilon

Practice Questions: Q3

Q3. A linear regression function assumes that the relation being modeled must be linear in:

A. both the variables and the coefficients.

B. the coefficients but not necessarily the variables.

C. the variables but not necessarily the coefficients.

D. neither the variables nor the coefficients.

Practice Questions: Q3 Answer

Explanation: B is correct.

Linear regression refers to a regression that is linear in the
coefficients/parameters; it may or may not be linear in the variables, which can enter a linear regression after appropriate transformation.

Module 2. Ordinary Least Squares Estimation

Topic 1. Ordinary Least Squares (OLS) Regression

Topic 2. Interpreting OLS Regression Results

Topic 3. Dummy Variables

Topic 4. Coefficient of Determination of a Regression

Topic 5. Assumptions Underlying Linear Regression

Topic 6. Properties of OLS Estimators

Topic 1. Ordinary Least Squares Regression

Purpose: Ordinary Least Squares (OLS) is a widely used method to estimate the parameters ( $α$ and $β$ ) in a regression equation.
Minimization Objective: OLS minimizes the sum of squared errors (residuals) in the sample data.
- Mathematically, OLS seeks to minimize:

Calculations for Simple Linear Regression:
- Slope Coefficient ( $β$ ): Describes the change in Y for a one-unit change in X.

Intercept Term ( $α$ ): The value of Y when X=0, representing the line's intersection with the Y-axis.
- The regression line estimated by OLS always passes through the point , which are the means of the independent and dependent variables, respectively.

\sum \epsilon_i^2=\sum[Y_i-(\alpha+\beta \times X_i)]^2

\beta=\frac{\sum_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{\sum_{i=1}^n\left(X_i-\bar{X}\right)^2}=\frac{\operatorname{Cov}(X, Y)}{\operatorname{Var}(X)}

\alpha=\bar{Y}-\beta \bar{X}

(\bar{X},\bar{Y})

Practice Questions: Q4

Q4. Ordinary least squares (OLS) refers to the process that:

A. maximizes the number of independent variables.

B. minimizes the number of independent variables.

C. produces sample regression coefficients.

D. minimizes the sum of the squared error terms.

Practice Questions: Q4 Answer

Explanation: D is correct.

OLS is a process that minimizes the sum of squared residuals to produce estimates of the population parameters known as sample regression coefficients.

Practice Questions: Q5

Q5. What is the most appropriate interpretation of a slope coefficient estimate equal to 10.0?

A. The predicted value of the dependent variable when the independent variable is zero is 10.0.

B. The predicted value of the independent variable when the dependent variable is zero is 0.1.

C. For every one unit change in the independent variable, the model predicts that the dependent variable will change by 10 units.

D. For every one unit change in the independent variable, the model predicts that the dependent variable will change by 0.1 units.

Practice Questions: Q5 Answer

Explanation: C is correct.

The slope coefficient is best interpreted as the predicted change in the dependent variable for a one-unit change in the independent variable. If the slope coefficient estimate is 10.0 and the independent variable changes by one unit, the dependent variable will change by 10 units. The intercept term is best interpreted as the value of the dependent variable when the independent variable is equal to zero.

Practice Questions: Q6

Q6. The mean inflation over the past 108 months is 0.01. Mean unemployment during that same time period is 0.044. The variance-covariance matrix for these variables is as follows:

What is the estimated slope coefficient and intercept, respectively?

A. 2.72 and −0.11.

B. 1.89 and 0.01.

C. 3.44 and −0.52.

D. 1.44 and 1.23.

(\bar{Y})

(\bar{X})

\left(\begin{array}{ll}\sigma_y^2 & \sigma_{xy}\\ \sigma_{xy} & \sigma_x^2 \end{array}\right)=\left(\begin{array}{ll}2.54 & 45.76 \\ 45.76 & 16.84 \end{array}\right)

Practice Questions: Q6 Answer

Explanation: A is correct.

\begin{aligned} & \beta=\frac{\operatorname{Cov}(\mathrm{X}, \mathrm{Y})}{\operatorname{Var} \mathrm{X}}=\frac{\sigma_{\mathrm{X}, \mathrm{Y}}}{\sigma_{\mathrm{X}}^2}=\frac{45.76}{16.84}=2.72 \\ & \alpha=\overline{\mathrm{Y}}-\beta \overline{\mathrm{X}}=0.01-2.72 \times 0.044=-0.11 \end{aligned}

Topic 2. Interpreting OLS Regression Results

Intercept Term ( $α$ ):
- Represents the value of the dependent variable when the independent variable(s) are equal to zero.
- Example: If market return is 0%, Stock A's return would be 4.9% (from the example calculation).
Slope Coefficient ( $β$ ):
- Represents the estimated change in the dependent variable for a one-unit change in that independent variable.
- Example: If $β = 0.73$ , a 1% increase in market returns would lead to a 0.73% increase in the stock's return.
- Multiple Independent Variables: In models with multiple independent variables, the slope coefficient for a given variable captures the change in the dependent variable for a one-unit change in that specific independent variable, while holding all other independent variables constant. These are sometimes called partial slope coefficients.

Topic 3. Dummy Variables

Definition: Dummy variables are independent variables that are binary in nature, taking on values of either 0 or 1.
Purpose: They are often used to quantify the impact of qualitative variables or categorical information.
Example:
- In a time series regression of monthly stock returns, a "January dummy variable" could be used.
- It would take a value of 1 if a stock return occurred in January, and 0 if it occurred in any other month.
- This allows analysis of whether stock returns in January are significantly different from returns in other months.

Topic 4. Coefficient of Determination of a Regression

Definition: The coefficient of determination, , measures the "fit" of the regression model.
Interpretation: It represents the proportion of the total variation in the dependent variable that is explained by the independent variable(s) in the model.
Single Explanatory Variable: For a regression model with only one independent variable, is simply the square of the correlation coefficient ( $r$ ) between the independent and dependent variables.
Implication of : If the slope coefficient is 0, implying no linear relationship between X and Y, then will also be 0, as variation in Y is unrelated to variation in X.

R^2

R^2=0

R^2=r_{X,Y}^2

R^2

Practice Questions: Q7

Q7. A researcher estimates that the value of the slope coefficient in a single explanatory variable linear regression model is equal to zero. Which one of the following is most appropriate interpretation of this result?

A. The mean of the Y variable is zero.

B. The intercept of the regression is zero.

C. The relation between X and Y is not linear.

D. The coefficient of determination of the model is zero.

(R^2)

Practice Questions: Q7 Answer

Explanation: D is correct.

When the slope coefficient is 0 , variation in Y is unrelated to variation in X and correlation . Therefore,

Alternatively, recall that . If and therefore:

r_{X, Y}=\frac{\operatorname{Cov}(X, Y)}{\sigma_X \sigma_Y}=\frac{0}{\sigma_X \sigma_Y}=0

r_{X, Y}=0

R^2=r^2{ }_{X, Y}=0

\beta=\frac{\operatorname{Cov}(X, Y)}{\operatorname{Var} X}

\beta=0, \operatorname{Cov}(X, Y)=0

Topic 5. Assumptions Underlying Linear Regression

OLS regression relies on several assumptions, primarily concerning the error term:
- Expected Value of Error Term is Zero: The expected value of the error term, conditional on the independent variable, is zero $[E (ϵ_{i} ∣ X_{i}) = 0]$ . This implies X provides no information about the error. Violations can include:
  - Survivorship/Sample Selection Bias: Observations are collected after the fact or contingent on specific outcomes.
  - Simultaneity Bias: X and Y values are determined simultaneously.
  - Omitted Variables: Important explanatory variables are not included, leading to biased coefficients.
  - Attenuation Bias: X variables are measured with error, leading to underestimation of coefficients.
- I.I.D. Observations: All (X, Y) observations are independent and identically distributed.
- Positive Variance of X: The variance of the independent variable (X) must be positive.
- Constant Variance of Errors (Homoskedasticity): The variance of the errors is constant across all levels of the independent variable.
- No large outliers: Large outliers are unlikely to be observed in the data. OLS estimates are sensitive to outliers, and large outliers have the potential to create misleading regression results.
Collectively, these assumptions ensure that the regression estimators are unbiased. Secondly, they ensure that the estimators are normally distributed and, as a result, allowed for hypothesis testing.

Topic 6. Properties of OLS Estimators

Random Variables: OLS estimators ( $α$ and $β$ ) are random variables themselves because they are derived from random samples and vary from sample to sample.
Sampling Distributions: Consequently, OLS estimators have their own probability distributions, known as sampling distributions. These distributions are crucial for estimating population parameters.
Unbiased Estimators: OLS estimators ( $α$ and $β$ ) are unbiased, meaning the expected value of the estimator is equal to the true population parameter.

Consistent Estimators: For large sample sizes, OLS estimators are consistent. A consistent estimator's accuracy increases as the sample size grows.
Normal Distribution: Given the Central Limit Theorem (CLT), for large sample sizes, the sampling distributions of OLS estimators will approach a normal distribution. This property is vital for statistical inference (e.g., hypothesis testing).
Reliability of Slope Coefficient: The variance of the slope ( $β$ ) increases with the variance of the error term, indicating lower reliability. The variance of the slope ( $β$ ) decreases with the variance of the explanatory variable (X), indicating higher reliability and confidence in the estimate.

(E(\hat{\alpha}=\alpha \text{ and } E(\hat{\beta})=\beta)

Practice Questions: Q8

Q8. The reliability of the estimate of the slope coefficient in a regression model is most likely:

A. positively affected by the variance of the residuals and negatively affected by the variance of the independent variables.

B. negatively affected by the variance of the residuals and negatively affected by the variance of the independent variables.

C. positively affected by the variance of the residuals and positively affected by the variance of the independent variables.

D. negatively affected by the variance of the residuals and positively affected by the variance of the independent variables.

Practice Questions: Q8 Answer

Explanation: D is correct.

The reliability of the slope coefficient is inversely related to its variance and the variance of the slope coefficient (β) increases with variance of the error term and decreases with the variance of the explanatory variable.

Module 3. Hypothesis Testing

Topic 1. Hypothesis Testing Procedure

Topic 2. Confidence Intervals

Topic 3. The p-value

Topic 1. Hypothesis Testing Procedure

Hypothesis testing for regression coefficients allows us to make inferences about the true population parameters.
Procedure:
1. Specify the Hypothesis: Define the null hypothesis ( $H_{0}$ ) and the alternative hypothesis ( $H_{A}$ ).
  - Example: versus
2. Calculate the Test Statistic: For regression coefficients, a t-statistic is typically used.
3. Make a Decision (Reject or Fail to Reject): Compare the absolute value of the calculated test statistic to a critical t-value (obtained from a t-table with $n - 2$ degrees of freedom and a chosen significance level).
  - If , reject the null hypothesis.
  - If , fail to reject the null hypothesis.

H_A: \beta \neq \beta_0

H_A: \beta = \beta_0

t=(\beta-\beta_0)/S_b

|t|>t_{critical}

|t| \leq t_{critical}

Topic 2. Confidence Intervals

Purpose: Confidence intervals provide a range of values within which the true population parameter (e.g., the slope coefficient) is likely to fall, with a certain level of confidence.
Formula: The confidence interval of the slope coefficient is calculated as:
- Confidence Interval
- Where:
  - is the estimated slope coefficient.
  - is the critical t-value for the given level of significance and degrees of freedom ( $n - 2$ ).
  - $S_{b}$ is the standard error of the slope coefficient.
Relationship to Hypothesis Testing:
- If the hypothesized value of the slope coefficient falls outside the confidence interval, you can reject the null hypothesis.
- If the hypothesized value falls inside the confidence interval, you fail to reject the null hypothesis.
- If you correctly rejected the null hypothesis that $β = 0$ in a hypothesis test, then zero should not fall within the calculated confidence interval.

\hat{\beta}

t_c

=\hat{\beta} \pm (t_c \times S_b)

Practice Questions: Q9

Q9. Bob Shepperd is trying to forecast 10-year T-bond yield. Shepperd tries a variety of explanatory variables in several iterations of a single-variable model. Partial results are provided below (note that these represent three separate one-variable regressions):

The critical t-value at 5% level of significance is equal to 2.02. For the regression model involving inflation as the explanatory variable, the confidence interval for the slope coefficient is closest to:

A. −0.27 to 2.43.

B. 0.26 to 2.43.

C. −2.27 to 2.43.

D. 0.22 to 1.88.

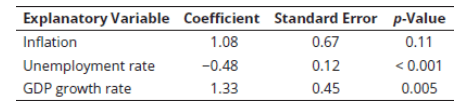
Practice Questions: Q9 Answer

Explanation: A is correct.

The confidence interval of the slope coefficient

or -0.27 to 2.43 . Notice that 0 falls within this interval and, hence, the coefficient is not significantly different from 0 at 5 % level of significance. The p-value of 0.11 (> 0.05) also gives the same conclusion.

=\beta \pm\left(\mathrm{t}_{\mathrm{c}} \times \mathrm{S}_{\mathrm{b}}\right)=1.08 \pm(2.02 \times 0.67)

Topic 3. The p-value

Definition: The p-value is the smallest level of significance at which the null hypothesis can be rejected.
Alternative Hypothesis Testing Method: Instead of comparing the test statistic to a critical value, you can compare the p-value to your chosen significance level:
- If p-value < Significance Level: Reject the null hypothesis.
- If p-value > Significance Level: Fail to reject the null hypothesis.
Common Practice: Regression outputs typically provide the p-value for the standard hypothesis ( $H_{0} : β = 0$ versus ).
Consistency: The p-value method will yield the same conclusion as the t-test method.

H_A: \beta \neq 0

Practice Questions: Q10

Q10. Bob Shepperd is trying to forecast 10-year T-bond yield. Shepperd tries a variety of explanatory variables in several iterations of a single-variable model. Partial results are provided below (note that these represent three separate one-variable regressions):

The critical t-value at 5% level of significance is equal to 2.02. For the regression model involving unemployment rate as the explanatory variable, what are the results of a hypothesis test that the slope coefficient is equal to 0.20 (vs. not equal to 0.20) at 5% level of significance?

A. The coefficient is not significantly different from 0.20 because the p-value is <
0.001.

B. The coefficient is significantly different from 0.20 because the t-value is 2.33, which is greater than the critical t-value of 2.02.

C. The coefficient is significantly different from 0.20 because the t-value is −5.67.

D. The coefficient is not significantly different from 0.20 because the t-value is
−2.33.

Practice Questions: Q10 Answer

Explanation: C is correct.

The p-value provided is for hypothesized value of the slope coefficient being equal to 0 . The hypothesized coefficient value is 0.20 .

\mathrm{t}=\frac{\beta-\beta_0}{\mathrm{~S}_{\mathrm{b}}}=\frac{-0.48-0.20}{0.12}=\frac{-0.68}{0.12}=-5.67

Practice Questions: Q11

Q11. Bob Shepperd is trying to forecast 10-year T-bond yield. Shepperd tries a variety of explanatory variables in several iterations of a single-variable model. Partial results are provided below (note that these represent three separate one-variable regressions):

The critical t-value at 5% level of significance is equal to 2.02. For or the regression model involving GDP growth rate as the explanatory variable, at a 5% level of significance, which of the following statements about the slope oefficient is least accurate?

A. The coefficient is significantly different from 0 because the p-value is 0.005.

B. The coefficient is significantly different from 0 because the 95% confidence interval does not include the value of 0.

C. The coefficient is significantly different from 0 because the t-value is 2.27.

D. The coefficient is not significantly different from 1 because t-value is 0.73.

Practice Questions: Q11 Answer

Explanation: C is correct.

When the p-value is less than the level of significance, the slope coefficient is significantly different from 0 . For the test of hypothesis about coefficient value significantly different from 0 :

The confidence interval of the slope coefficient

or 0.42 to 2.34. 0 is not in this confidence interval.

For hypothesis test of coefficient is equal to 1 :

\mathrm{t}=\frac{\beta-\beta_0}{\mathrm{~S}_{\mathrm{b}}}=\frac{1.33-0}{0.45}=2.96

=\beta \pm\left(t_c \times S_b\right)=1.33 \pm(2.02 \times 0.45)

\mathrm{t}=\frac{\beta-\beta_0}{\mathrm{~S}_{\mathrm{b}}}=\frac{1.33-1}{0.45}=0.73