2307588

FALL 2021

MACHINE LEARNING

FOR GEOSCIENCES

calendar

Aug
Sept
Oct
Nov
Dec
12 first-day class
midterm
Oct 07
CH 1
CH 1
no class
CH 4
CH 4
CH 3
CH 2
final
Dec 02
no class
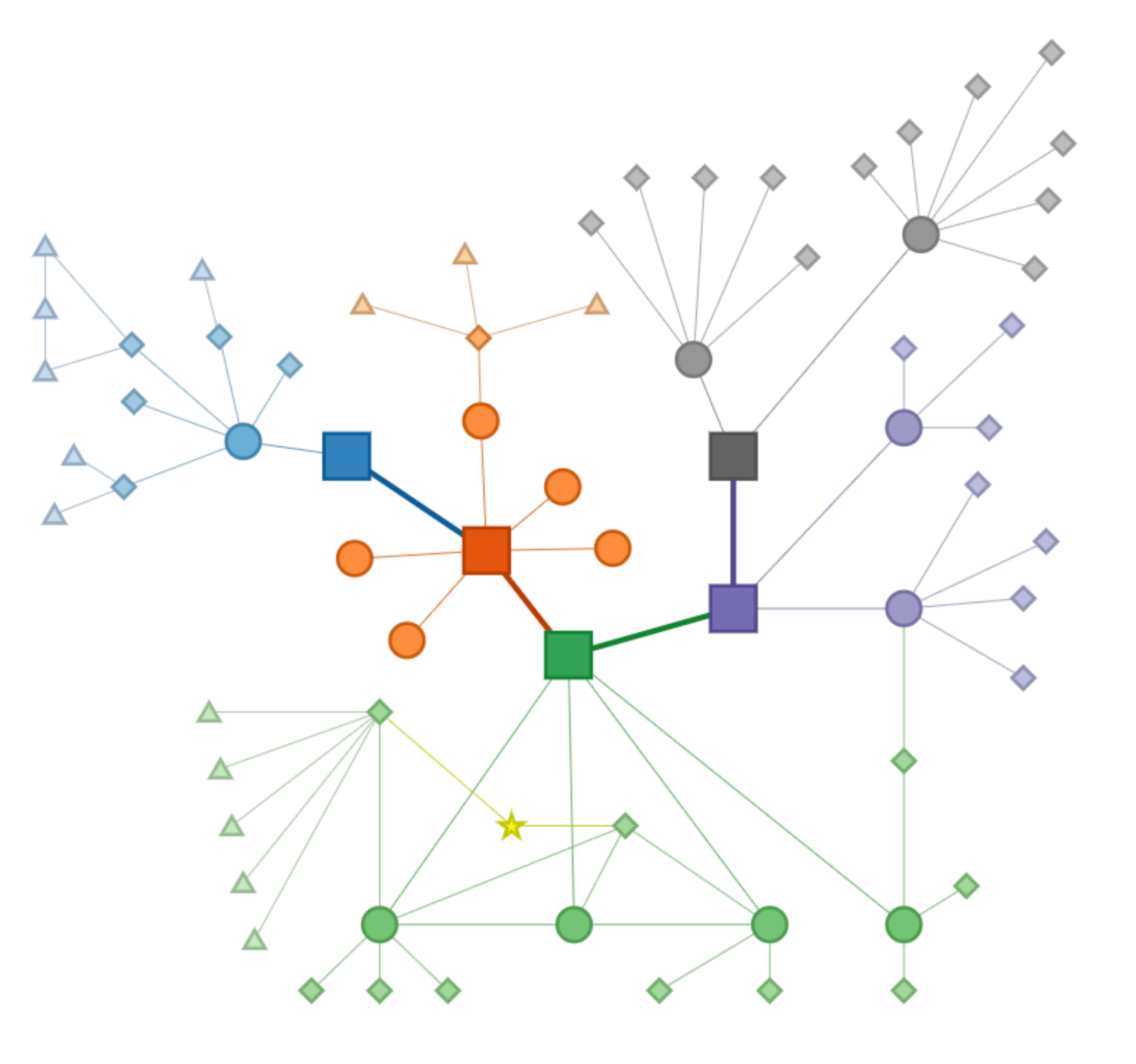
CH 5
CH 5
CH 6
CH 7
CH 7
CH 7

ITINERARY (MIDTERM)

MIDTERM PROJECT

ECOSYSTEM

CH: 0

INTRODUCTORY PYTHON

CH: 1

INTRODUCTORY MACHINE LEARNING

CH: 2

PREPROCESSING DATA

CH: 3

AUTOMATIC MACHINE LEARNING

CH: 4

ITINERARY (FINAL)

HYPERPARAMETER TUNING

CH: 6

GREDIENT BOOSTED DECISION TREES

CH: 5

HANDON FINAL PROJECT

GAUSSIAN PROCESS REGRESSION

CH: 7

ML and DL for Geosciences

MACHINE LEARNING

AUTOMATIC ML

class 2307588
class 2307589

DEEP

LEARNING

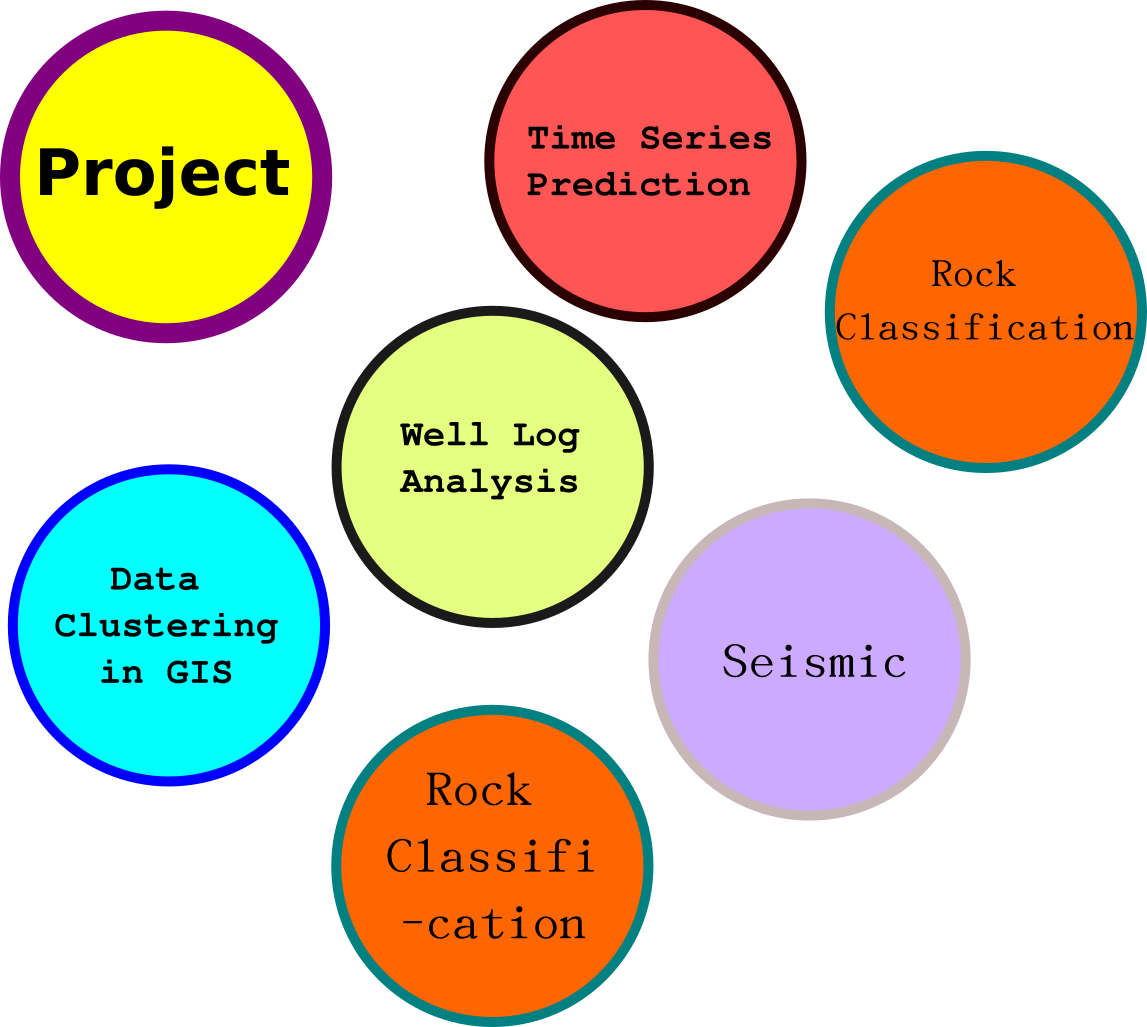
Time Series Prediction
Well Log Analysis
Data 
Clustering
in GIS

Microscope/fossils

Seismic

Rock

Classification

Grading Policy

midterm 30%

final 60%

RULES:

project based learning

bonus 10%

  • always on time
  • behave like sit-in class
  • absent more than 2 times, you will lose bonus score
  • always on camera (is a must)...I want to observe that you didn't sleep during class
  • no phone during class 
  • please stay at home or properly studied environment... not coffee shop, beach, restaurant...keep in mind that you have responsibility to answer your friends and instructor's questions
  • dress properly

Ecosystem

 Installations

Classic Equation

F = M \times A + (\alpha 1 + \beta 1)

neuron networks

Modern Equation

the network equations that human can program 
a computer to know how to learn

artificial intelligence 

machine learning

deep learning

AutoML

supervised learning

unsupervised learning

 A Broader Family of ML Methods

(based on artificial neural networks)

Supervised Learning vs Unsupervised Learning

Classifcation

Latent Space in ML

Course Overview

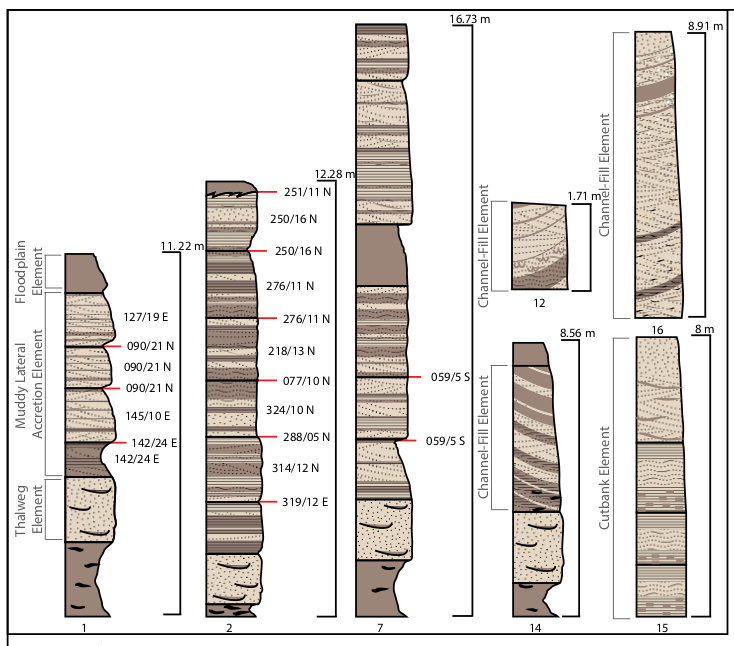
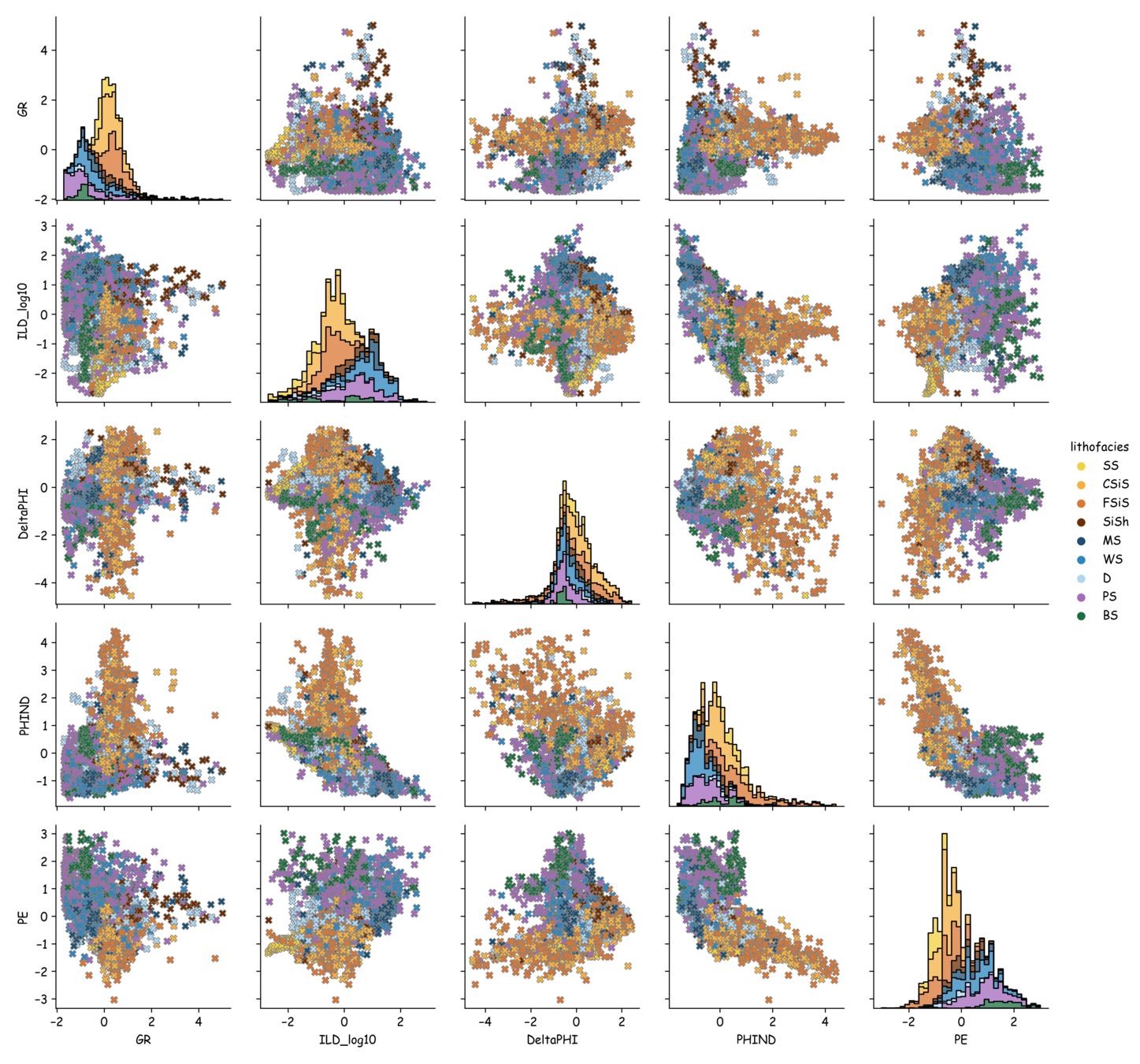
The figures show that the intervals contain sequence stratigraphy of fluvial environment exposed to the surface. Geoscientists can interpret the rocks based on colors, gain sizes, and minerals. So how can we obtain the subsurface information?


In order to obtain that information, geoscientists deploy wirelines into a borehole to measure a formation property. Each rock layer contained different kinds of minerals that possess distinguishable characteristics. However, their properties are not discrete, which requires tremendous works to classify. Here, we will follow the SEG competition 2016 to study ML/AutoML workflow to create a robotized framework of petrophysical analysis.

CH 1: INTRODUCTORY PYTHON

Introductory Python

variables and assignment

>>> a = 10
>>> a
>>> 10

Value 10 is assigned as "=" assignment operator into variable a, and variable a will be stored value 10 in memory space in the computer. When compiling variable a, the program will return value of 10.

update variables and re-assignment

>>> a = a + 2
>>> a
>>>

Let us try to modify the variable that previously stores value 10 in the memory allocation, and this time add a new value (2) into the previous variable a. What is the outcome? All variables and values are input on the right-hand side of this code snipped, and the left-hand side is output stored in the assigned variable named a.

check your understanding

>>> a = a + 4
>>> b = a + 3
>>> a
>>> b

Think about the result and try to explain what variable a and b has been stored.

What is binary?

Did you know? Computer uses the number only 0 and 1 to computerize

Data Types in Python

string
tuple
set
dictionary
numpy array
data 

structure
class 
and 
object
list
matrix
vector
numeric precision
float
integer
complex
bit (byte)

If Statement and For Loop

A > 80
70 < B <= 80
60 < C <= 70
50 < D <= 60
F <= 50
score = 67

if score > 80:
  print('your grade is A')
score = [45, 78, 7, 66, 89]

for i in score:
	if i > 80:
		print('your score is A')

create for loops with statement conditions to compute the average score of this data.

score = [34, 55, 67, 78, 99, 100, 45, 35.9, 88.45, 89]

Built-In Function and Defining Function

Try to plot cosine and sine functions

built-in function

 Indexing and Row-Column-Major Order

To access element in Python, we need to understand the reference of data position (indexing) and direction to reach the data (row-column-major order). Indexing in Python refers to the position of the memory allocation. By default (Python), it counts the data from "0" and increasing by one. To optimize the speed of accessing element in Python, we should reach the data in row-column major.
 
 
 
row-column-major order
indexing 
(2-D)
\mathbf{a_{0, 0}}
\mathbf{a_{0, 1}}
\mathbf{a_{0, 2}}
\mathbf{a_{0, 3}}
\mathbf{a_{1, 0}}
\mathbf{a_{2, 0}}
\mathbf{a_{3, 0}}
\mathbf{a_{1, 1}}
\mathbf{a_{1, 2}}
\mathbf{a_{1, 3}}
\mathbf{a_{2, 1}}
\mathbf{a_{2, 2}}
\mathbf{a_{2, 3}}
\mathbf{a_{3, 1}}
\mathbf{a_{3, 2}}
\mathbf{a_{3, 3}}
row (i)
col (j)
indexing 
(3-D)
\mathbf{a_{0, 0}}
\mathbf{a_{0, 1}}
\mathbf{a_{0, 2}}
\mathbf{a_{0, 3}}
\mathbf{a_{1, 0}}
\mathbf{a_{2, 0}}
\mathbf{a_{3, 0}}
\mathbf{a_{1, 1}}
\mathbf{a_{1, 2}}
\mathbf{a_{1, 3}}
\mathbf{a_{2, 1}}
\mathbf{a_{2, 2}}
\mathbf{a_{2, 3}}
\mathbf{a_{3, 1}}
\mathbf{a_{3, 2}}
\mathbf{a_{3, 3}}
col (j)
3-D (k)

Indexing and Slicing Numpy Arrays

10

34

2

0

66

31

9

5

import numpy as np

x = np.array([0, 10, 34, 2, 5, 66, 31, 9])

note: () - tuple stores array []

1

2

3

0

5

6

7

4

-7

-6

-5

-8

-3

-2

-1

-4

value

index

index

import numpy as np

x = np.array([0, 10, 34, 2, 5, 66, 31, 9])

print(x[0])
print(x[-1])
print(x[3:6])
print(x[-1:-4])

10

34

2

0

66

31

9

5

57

79

11

4

0

3

7

39

-7

-6

-5

-8

58

-2

-1

-4

i

j

Let us try to access the data in 2D array

10

34

2

0

66

31

9

5

57

79

11

4

0

3

7

39

-7

-6

-5

-8

58

-2

-1

-4

i

j

Building Layered Models

Try to reproduce the two figures below. Click the GitHub icon to access the guideline on how to reproduce both models.

layered_model

Pandas-Dataframe

Facies Formation Well Name Depth GR ILD_log10 DeltaPHI PHIND PE NM_M RELPOS
3 A1 SH SHRIMPLIN 2793 77.45 0.664 9.9 11.915 4.6 1 1
3 A1 SH SHRIMPLIN 2793.5 78.26 0.661 14.2 12.565 4.1 1 0.979
3 A1 SH SHRIMPLIN 2794 79.05 0.658 14.8 13.05 3.6 1 0.957
3 A1 SH SHRIMPLIN 2794.5 86.1 0.655 13.9 13.115 3.5 1 0.936
3 A1 SH SHRIMPLIN 2795 74.58 0.647 13.5 13.3 3.4 1 0.915
3 A1 SH SHRIMPLIN 2795.5 73.97 0.636 14 13.385 3.6 1 0.894
3 A1 SH SHRIMPLIN 2796 73.72 0.63 15.6 13.93 3.7 1 0.872
3 A1 SH SHRIMPLIN 2796.5 75.65 0.625 16.5 13.92 3.5 1 0.83
3 A1 SH SHRIMPLIN 2797 73.79 0.624 16.2 13.98 3.4 1 0.809

In case we would like to work with tabular data. Note that we can create tabular data used Python by creating dictionary.

Pandas data frame (exploring data)

Pandas data frame (data visualization)

Understanding the Data in Numpy Array (1D)

Python provides a basic built-in function that we can use for computing sine and cosine functions. Here, we are going to re-create the 3 functions and try to solve the problem with more than one solution. Let us see Github for guideline.

Let us reproduce all figures

sin_cos

Understanding the Data in Numpy Array (2D)

0.02

0.07

0.27

0.09

0.55

0.21

0

1

2

...

 

 

840

918

pixel-y

amplitude

row

0.01

0.21

0.29

0.49

0.03

0.13

0.14

0.33

0.93

0.94

0.89

0.19

0.77

0.56

0.28

0.73

0.01

0.21

0.29

0.49

0.03

0.3

0.14

0.33

0.93

0.94

0.89

0.9

0.77

0.56

0.28

0.23

0.01

0.51

0.55

0.49

0.03

0.13

0.14

0.3

0.93

0.94

0.89

0.58

0.77

0.31

0.28

0.1

col

Check your understanding

Let us crop one oxbow from the image 2D, and then extract only the waterbody.

Hint (1) use the if statement to suppress the unwanted areas. Once you extracted the waterbody successfully, you can count the number of pixels to estimate the size of the waterbody. Hint (2) use for-loop to count values in the 2D matrix that is larger and equal to your waterbody values.

oxbow

oxbow

Flatten Matrix to Sequential Order (Vector)

\mathbf{A} \in \mathbb{R}^{4\times 3}
\mathbf{a_{0, 1}}
\mathbf{a_{0, 2}}
\mathbf{a_{1, 0}}
\mathbf{a_{1, 1}}
\mathbf{a_{1, 2}}
\mathbf{a_{2, 0}}
\mathbf{a_{2, 1}}
\mathbf{a_{2, 2}}
\mathbf{a_{3, 0}}
\mathbf{a_{3, 1}}
\mathbf{a_{3, 2}}
\mathbf{a} \in \mathbb{R}^{12}
\mathbf{a_{0, 1}}
\mathbf{a_{0, 2}}
\mathbf{a_{1, 1}}
\mathbf{a_{1, 2}}
\mathbf{a_{2, 0}}
\mathbf{a_{2, 1}}
\mathbf{a_{2, 2}}
\mathbf{a_{3, 0}}
\mathbf{a_{3, 1}}
\mathbf{a_{3, 2}}
\mathbf{a_{1, 0}}
\mathbf{a_{0, 0}}
\mathbf{a_{0, 0}}
reshape
\mathbf{a_{0, 1}}
\mathbf{a_{0, 2}}
\mathbf{a_{1, 0}}
\mathbf{a_{1, 1}}
\mathbf{a_{1, 2}}
\mathbf{a_{2, 0}}
\mathbf{a_{2, 1}}
\mathbf{a_{2, 2}}
\mathbf{a_{3, 0}}
\mathbf{a_{3, 1}}
\mathbf{a_{3, 2}}
\mathbf{a} \in \mathbb{R}^{12}
\mathbf{a_{0, 1}}
\mathbf{a_{0, 2}}
\mathbf{a_{1, 1}}
\mathbf{a_{1, 2}}
\mathbf{a_{2, 0}}
\mathbf{a_{2, 1}}
\mathbf{a_{2, 2}}
\mathbf{a_{3, 0}}
\mathbf{a_{3, 1}}
\mathbf{a_{3, 2}}
\mathbf{a_{1, 0}}
\mathbf{a_{0, 0}}
\mathbf{a_{0, 0}}
reshape

(flatten)

\mathbf{A} \in \mathbb{R}^{4\times 3}
One of the most common technique in ML that has many applications such as speed up the ccomputation, sinking high-dimentional space into vector for compuation.

Show me how you flatten the 2D array

import numpy as np

x = np.array([1, 2, 3, 4, 12, 4.6, -2])
y = np.array([5, 8, 9, -1, -8.3, 2.6, 0])

dummy_of_2D = np.zeros(shape=(len(y), len(x)), dtype=float)
for col in range (0, len(x)):
    print('second loop x =', x[col])
    for row in range (0, len(y)):
        # print('first loop x =', x[col], 'first loop y =', y[row])
        dummy_of_2D[row, col] =+ x[col] + y[row]
print(dummy_of_2D.shape)
print(dummy_of_2D)

Flatten Matrix to Sequential Order (Vector)

Revisit Latent Space

255

208

2

255

127

255

106

255

8

255

vector

latent

Game for Weekend

x < 4.2
A > 80
A > 80

0

2

4

6

8

2

4

6

8

10

CH 2: INTRODUCTORY

MACHINE LEARNING

ML Timeline

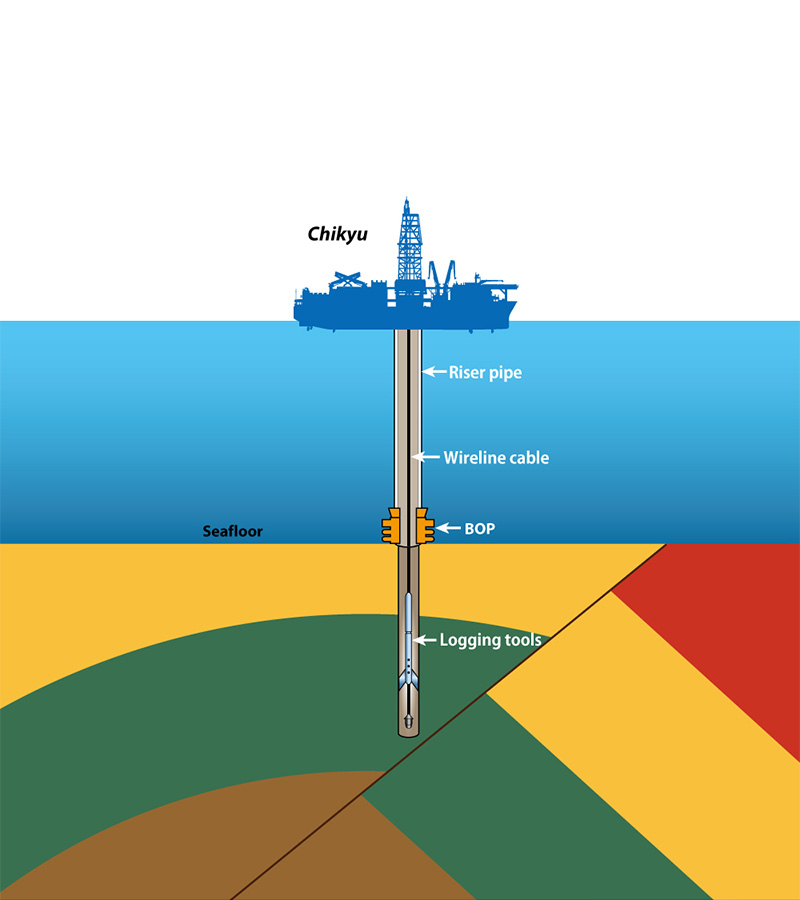
Extracting Subsurface Information Using Well Logs

Data Types: Tabular (Well Logs)

Facies Formation Well Name Depth GR ILD_log10 DeltaPHI PHIND PE NM_M RELPOS
3 A1 SH SHRIMPLIN 2793 77.45 0.664 9.9 11.915 4.6 1 1
3 A1 SH SHRIMPLIN 2793.5 78.26 0.661 14.2 12.565 4.1 1 0.979
3 A1 SH SHRIMPLIN 2794 79.05 0.658 14.8 13.05 3.6 1 0.957
3 A1 SH SHRIMPLIN 2794.5 86.1 0.655 13.9 13.115 3.5 1 0.936
3 A1 SH SHRIMPLIN 2795 74.58 0.647 13.5 13.3 3.4 1 0.915
3 A1 SH SHRIMPLIN 2795.5 73.97 0.636 14 13.385 3.6 1 0.894
3 A1 SH SHRIMPLIN 2796 73.72 0.63 15.6 13.93 3.7 1 0.872
3 A1 SH SHRIMPLIN 2796.5 75.65 0.625 16.5 13.92 3.5 1 0.83
3 A1 SH SHRIMPLIN 2797 73.79 0.624 16.2 13.98 3.4 1 0.809

numberic data

integer

floating-point

categorical data

binary

muticlass

text

string

Facies: 3, NM_M: 1

Depth: 2793.0, GR: 78.26 

Facies: 2 classes

Facies: 9 classes

data

types

Well Name: SHRIMPLIN

Data Correlation (Scatter Plot)

Tabular data provide a lot of information contained multiple rows and columns, and these big data might need to decompose into a scatter plot to gain more understanding about the data. Here, we analyze the relationship between ILD and GR. Note that one log penetrates through multi-layers of rocks showing on the left diagram as multiple colors.

Let us try to reproduce the figure. Note that if you would like to sampling data such as every 10 data points and show only one point, you can use "data = data[::10]".

scatter

Data Correlation (Linear Regression)

input data

create line to fit

measuring the error

find the best fit

\Delta x
\Delta y
slope = \Delta x / \Delta y
intercept = line\ cross\ axis-y

linear regression

Unsupervised Learning (K-means)

input data

locate centroids

measure distances

relocate centroids

distance equal threshold

end

yes

no

find the shortest paths between each data point and centroid.

yes/no condition, the program will end if the shortest distances between centroids and data points equal the threshold (near 0)

done! good job

Demo K-Means

kmeans

Supervised Learning (Decision Tree)

classify granite and sandstone 

grain size

<0.1

>=0.1

color

white-like

dark-like

density

mineral

>=2.60

hardness

<2.60

Mohs = 1

Mohs = 7

Mohs = 10

quartz

felspar

granite

sandstone

keep in mind that we can not classify granite and sandstone such as these simple rules.

balanced decision trees

1

2

4

3

Decision Tree (Example)

preview a result from this exercise

decision tree

CH 3: PREPROCESSING DATA

Normalization

normalization

Outliers

outlier

Demo Normalization and Outliers

drop outlier

normalization

Preprocessing Data

missing values

normalization

outliers

categorical transformation

Facies Formation Well Name Depth GR ILD_log10 DeltaPHI PHIND PE NM_M RELPOS
sand A1 SH SHRIMPLIN 2793 77.45 0.664 9.9 11.915 4.6 1 1
shale A1 SH SHRIMPLIN 2793.5 78.26 0.661 14.2 12.565 4.1 1 0.979
dolomite A1 SH SHRIMPLIN 2794 79.05 0.658 14.8 13.05 3.6 1 0.957
sand A1 SH SHRIMPLIN 2794.5 86.1 0.655 13.9 100 3.5 1 0.936
shale A1 SH SHRIMPLIN 2795 74.58 0.647 13.3 3.4 1 0.915
limestone A1 SH SHRIMPLIN 2795.5 73.97 0.636 14 13.385 3.6 1 0.894
dolomite A1 SH SHRIMPLIN 2796 73.72 0.63 15.6 13.93 3.7 1 0.872
sand A1 SH SHRIMPLIN 2796.5 75.65 0.625 16.5 13.92 3.5 1 0.83
sand A1 SH SHRIMPLIN 2797 73.79 0.624 16.2 13.98 3.4 1 0.809

-999

(13.9+14)/2

Facies categorical transformation
sand 1
shale 2
dolomite 3
sand 1
shale 2
limestone 4
dolomite 3
sand 1
sand 1

min

max

-1

1

73.72

0.624

86.1

0.664

75.65

0.647

???

Demo Missing Value in Decision Tree

import data

step 1

preprocessing data

step 2

split data

step 3

  decision tree  


 evaluate model 

step 4

step 5

PE miss_value
4.6 0
4.1 0
3.6 0
-999 1
-999 1
-999 1
-999 1
-999 1
-999 1

try to compare between add one more column of missing value and without adding the column

try to compare between add one more column of missing value and without adding the column

 

This time change ratio of splitting data and max depth 

Note that this demo preprocessing only missing values by adding one column. Future work can apply dropping outliers, normalization, etc.

decision tree

missing value

1. Binomial classification: predicting two-class (e.g., yes or no)

2. Multinomial classification: predicting more than two-class

3. Hybrid to binary: force predicting of more classes into two classes

    3.1 one vs the rest

    3.2 one? vs one?

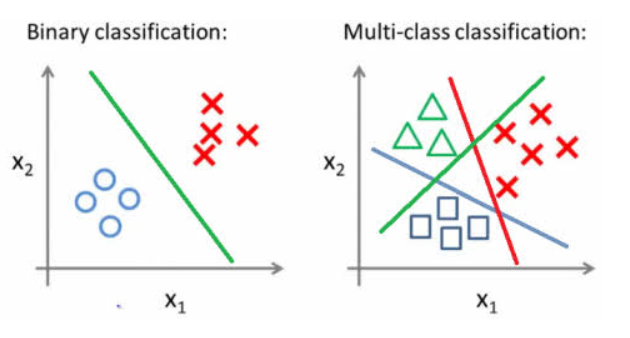
3 Types of Classification Methods in AutoML

Demo Missing Value in Decision Tree

import data

step 1

preprocessing data

step 2

split data

step 3

  decision tree  


 evaluate model 

step 4

step 5

step 4

CH 4: AUTOMATIC

MACHINE LEARNING

How Does AutoML Improve Pipeline in ML/DL?

input data

feature engineering

inference

evaluation metrics

ML Model(s)

inference

SVM

GTB

K-means

AutoML

lightGBM

RF

 neuron network

XGBoost

CatBoost

algorithm selection with optimized parameters

The Past, Present, Future of AutoML

A Demo Project on Well Log Analysis

The figures show that the intervals contain sequence stratigraphy of fluvial environment exposed to the surface. Geoscientists can interpret the rocks based on colors, gain sizes, and minerals. So how can we obtain the subsurface information?


In order to obtain that information, geoscientists deploy wirelines into a borehole to measure a formation property. Each rock layer contained different kinds of minerals that possess distinguishable characteristics. However, their properties are not discrete, which requires tremendous works to classify. Here, we will follow the SEG competition 2016 to study ML/AutoML workflow to create a robotized framework of petrophysical analysis.

AutoML Pipeline

input data

continued

lithofacies

well log (Newby)

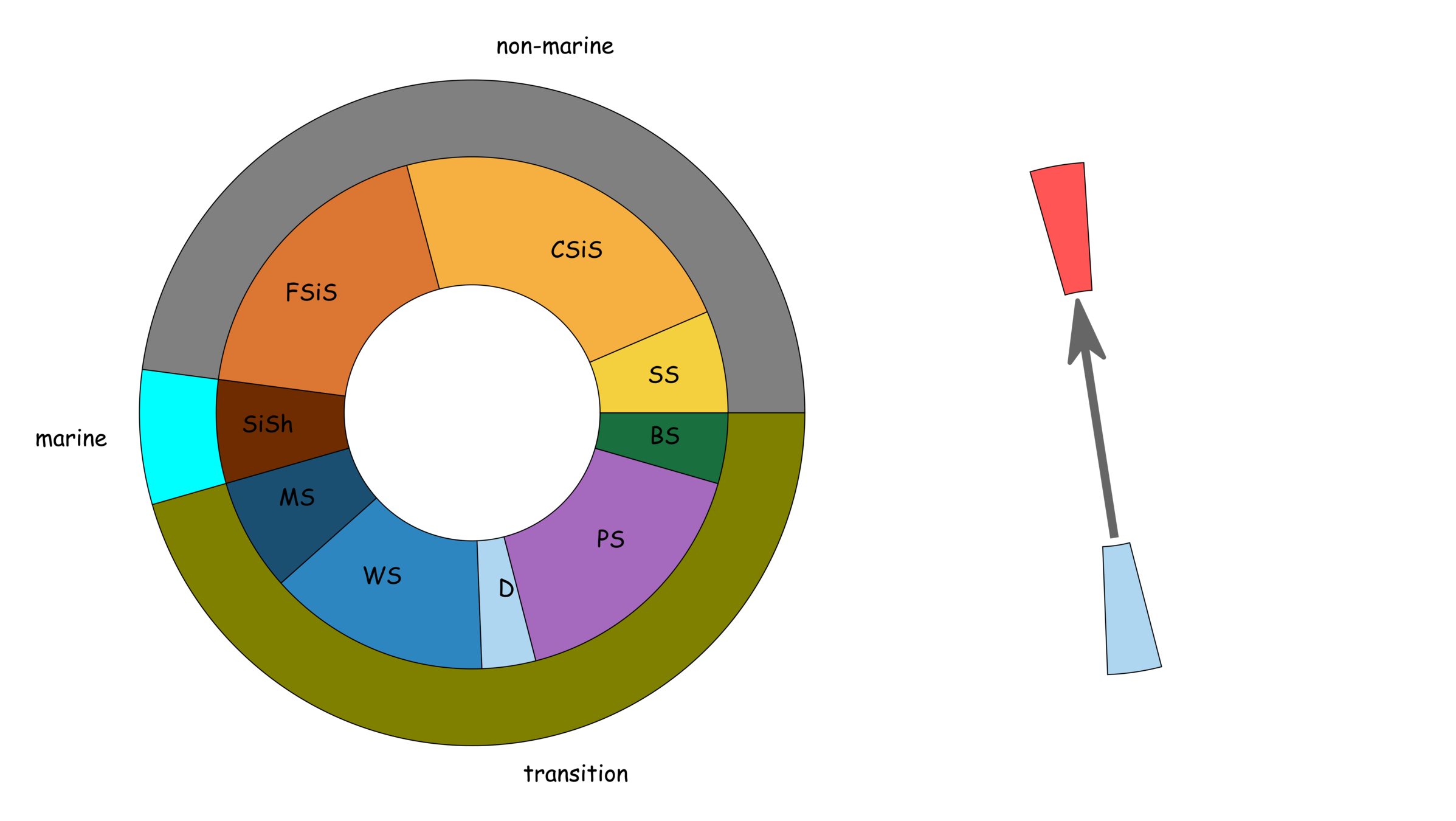
pairplots with normal distributions

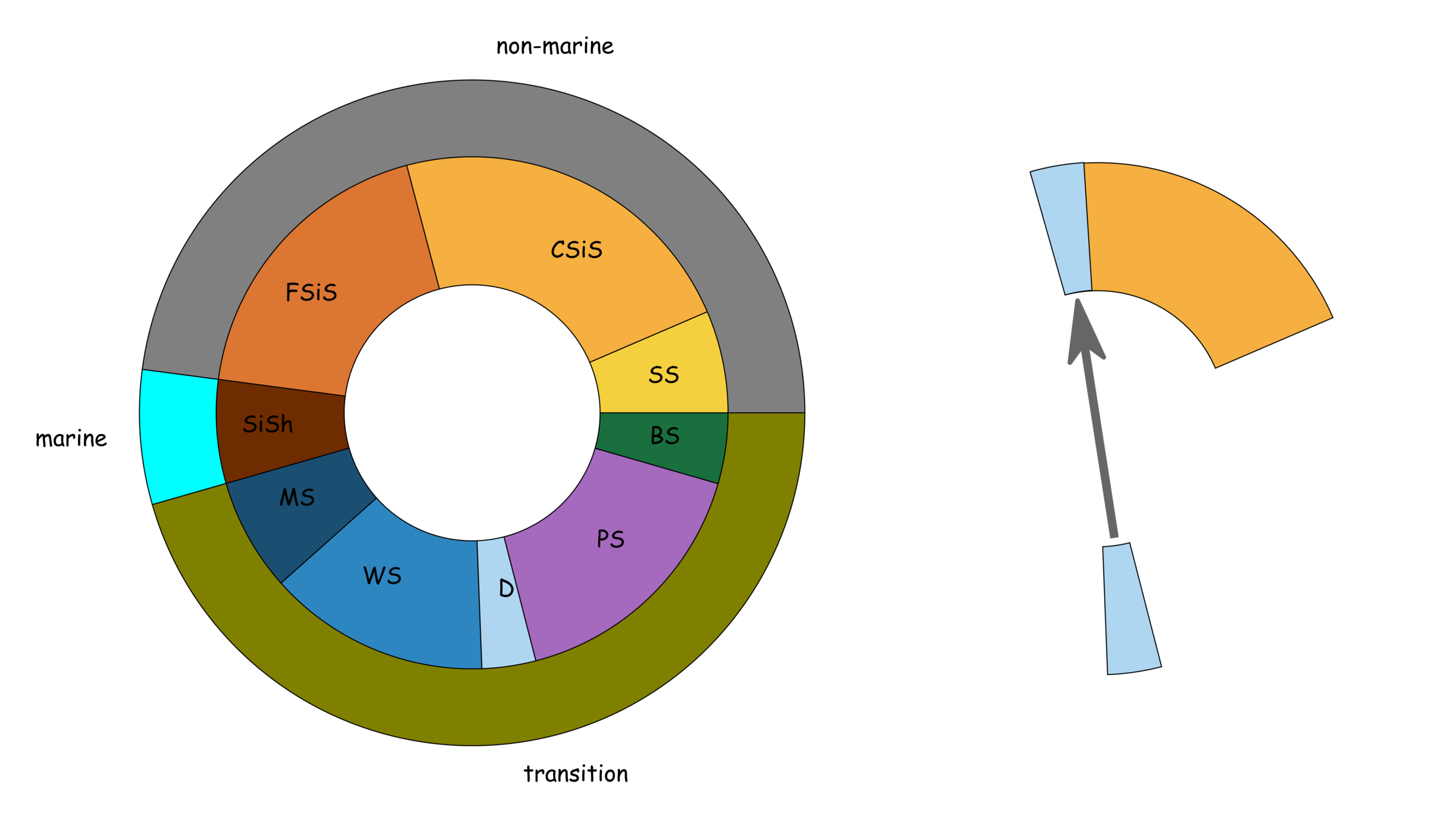
Facies description labels with adjacent facies

 

1

Nonmarine sandstone

 

2

2

Nonmarine course siltstone               

 

1,3

3

Nonmarine fine siltstone

 

2

4

Marine siltstone and shale

 

5

5

Mudstone

 

4,6

6

Wackestone

 

5,7,8

7

Dolomite

 

6,8

8

Packstone-grainstone

 

6,7,9

9

Phylloid-algal bafflestone

 

7,8

SS

CSiS

FSiS

SiSh

MS

WS

D

PS

BS

non-marine

marine

transition

input data
continued

feature engineering

2021-07-09T12:23:48.419393 image/svg+xml Matplotlib v3.4.2, https://matplotlib.org/

raw data

preprocessed data

input data
continued

AutoML

feature engineering

split data by wells

split data by fraction (80%)

training data

validated data

test

NEWBY

LUKE G U

CROSS H CATTLE

SHANKLE

SHRIMPLIN

Recruit F9

NOLAN

ALEXANDER D

CHURCHMAN BIBLE

KIMZEY A

split data by fraction (20%)

training data (80%)

validating data (20%)

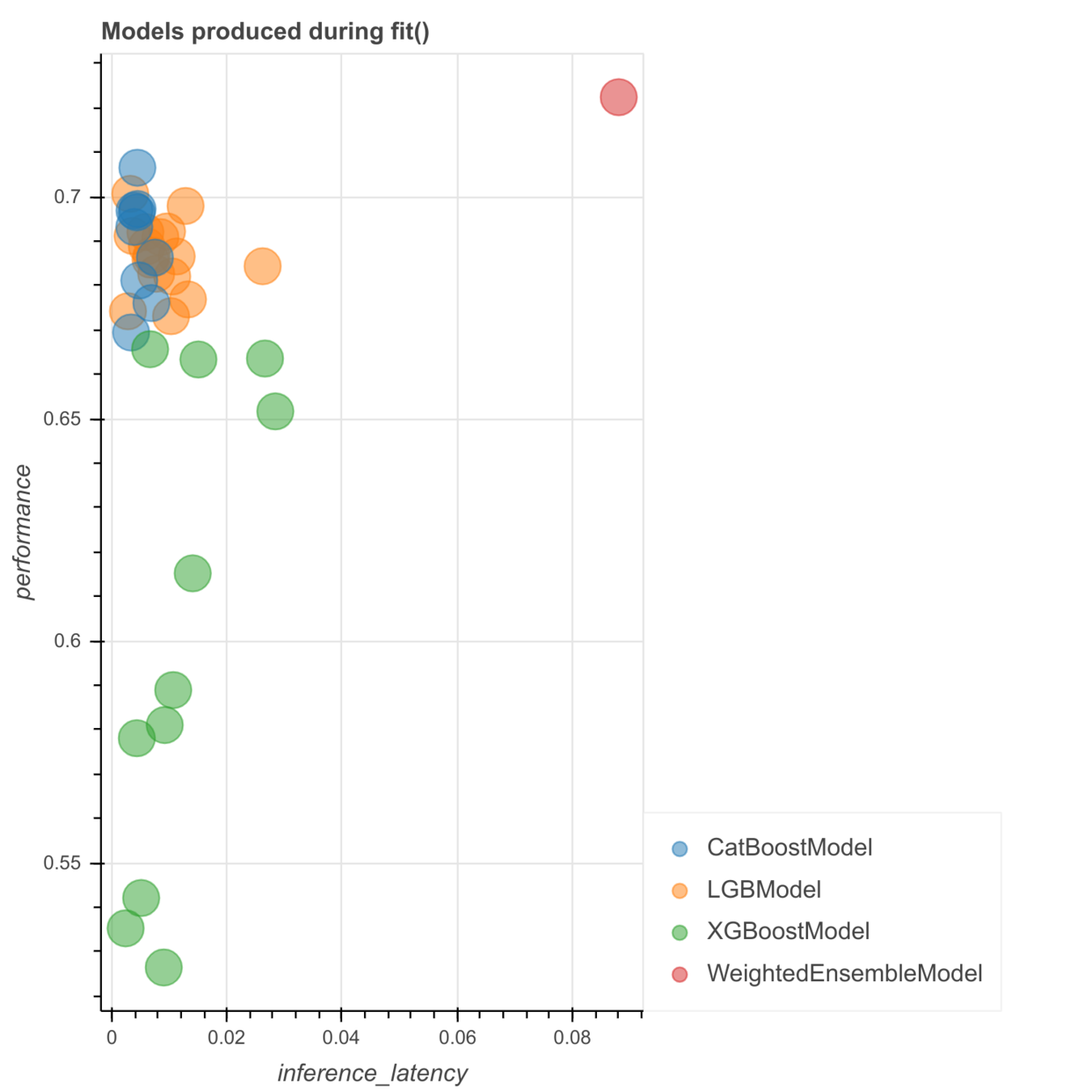
model list (top 5)

  1. CatBoost

  2. XGBoost

  3. LightGBM

  4. RandomForest

  5. NeuralNetFastAI 

model ensembling with stacking/bagging

models in AutoML

input data
continued
feature engineering

confusion matrix (WeightedEnsemble_L3)

evaluation metrics

AutoML
input data
feature engineering
AutoML

trained models

evaluation metrics

Done! GOOD JOB

Weighted_Ensemble_L3 (f1 macro: 0.311)

2021-07-09T15:37:32.737673 image/svg+xml Matplotlib v3.4.2, https://matplotlib.org/

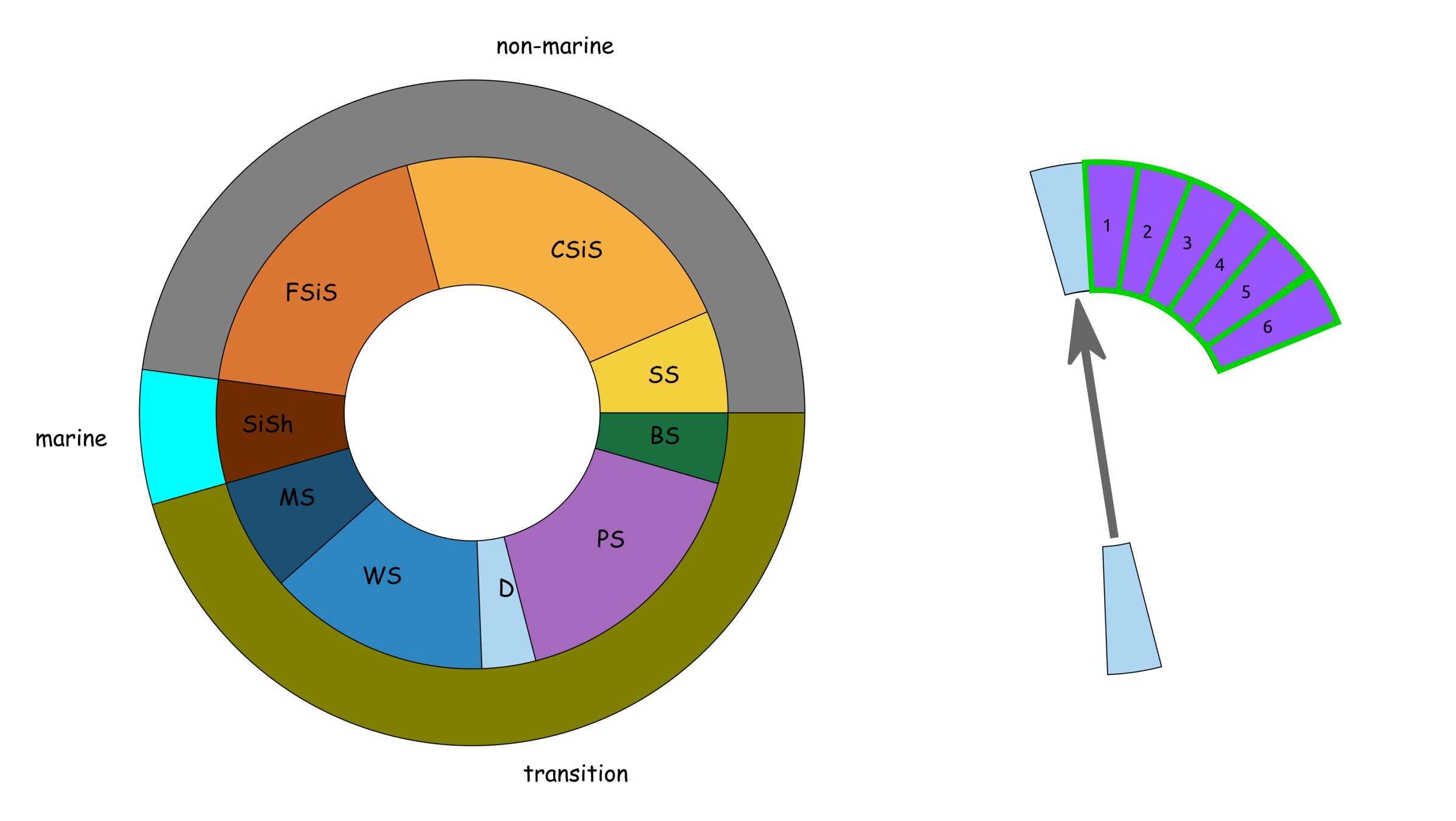
Facies description labels with adjacent facies

 

1

Nonmarine sandstone

 

2

2

Nonmarine course siltstone               

 

1,3

3

Nonmarine fine siltstone

 

2

4

Marine siltstone and shale

 

5

5

Mudstone

 

4,6

6

Wackestone

 

5,7,8

7

Dolomite

 

6,8

8

Packstone-grainstone

 

6,7,9

9

Phylloid-algal bafflestone

 

7,8

SS

CSiS

FSiS

SiSh

MS

WS

D

PS

BS

data visualization

AutoML

Confusion Matrix (Binary)

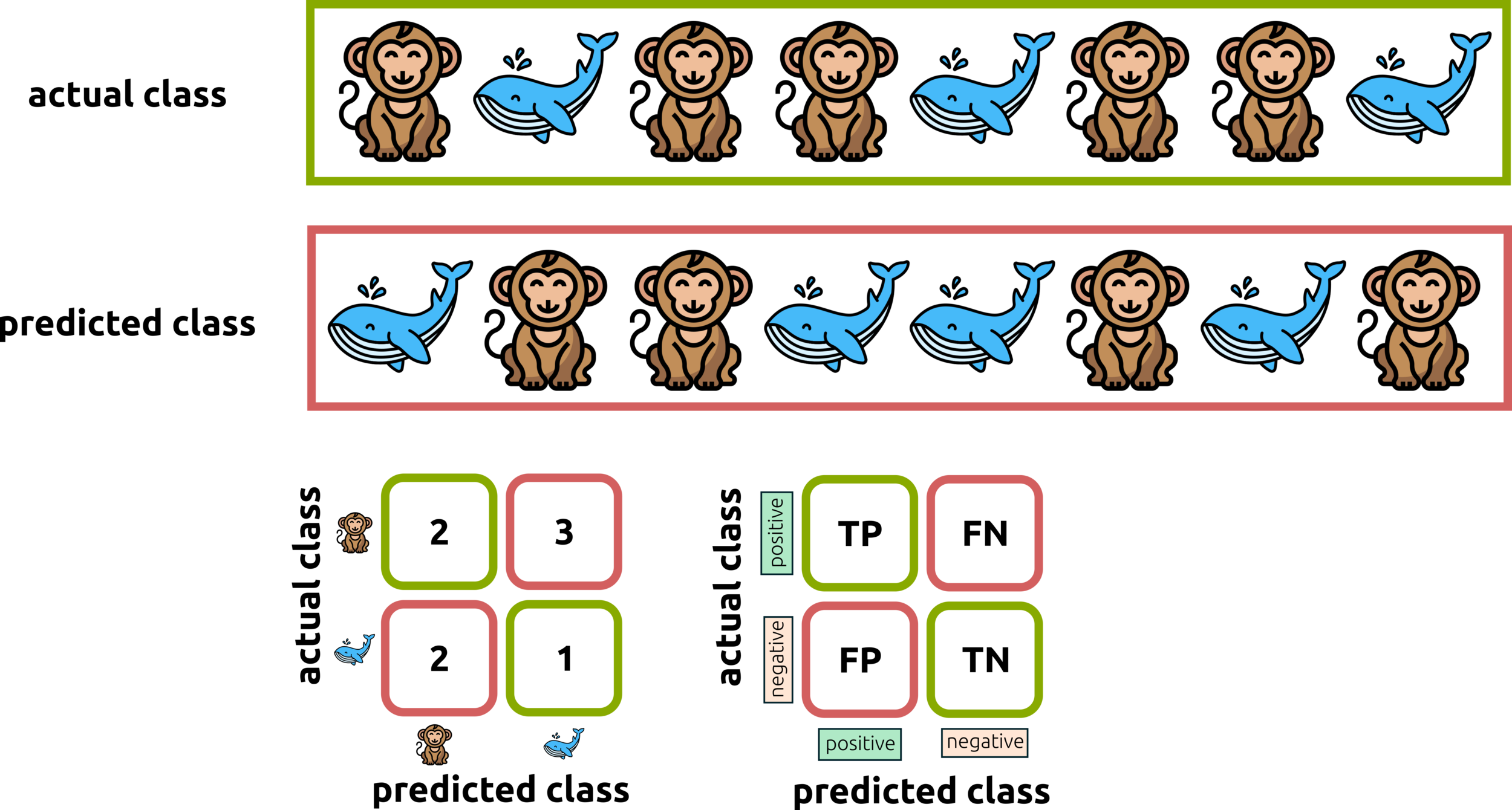
we are looking for monkey and non-monkey

Confusion Matrix (Multi-Class Classification)

prediction

TRUE POSITIVE (TP) = 10

true

hydrocarbon

brine

unsaturation

unsaturation

10

8

1

hydrocarbon

43

20

50

brine

6

70

100

unsaturation

TRUE NEGATIVE (TN) = 20+50+70+100

FALSE NEGATIVE (FN) = 43+6

FALSE POSITIVE (FP) = 8+1

Consider class-by-class (hydrocarbon)

prediction

Global and Macro Scores (All Classes vs Single Class)

\displaystyle precision=\frac{TP}{TP+FP}
\displaystyle recall=\frac{TP}{TP+FN}
\displaystyle F-1\ score=\frac{2TP}{2TP+FP+FN}
class
precision
recall
F-1 score
hydrocarbon
brine
unsaturation

CH 5: GRADIENT BOOSTED DECISION TREES (GBDTs)

Linear Regression and Gradient Descent

Linear Regression and Gradient Descent

Gradient Boosting Methods

input data

feature engineering

evaluation metrics

AutoML

trained models

gradient boosting methods

CatBoost

XGBoost

lightGBM

model ensembling with stacking/bagging

hyperparameter tuning

CatBoost: Gradient Boosting with

Categorical Features Support

balanced decision trees

1

2

4

3

Label-Encoding and One-Hot-Encoder

To improve the efficiency of the gradient boosting methods, we should convert all columns containing categorical data into numeric data. Label-encoding and one-hot-encoder aim to treat this problem. Label-encoding can convert categorical data into numeric data having sequential values. However, this method might implement a bias weight into a more considerable value. To overcome this problem, we use a one-hot-encoder to distribute the converted numeric column from label-encoder to have more columns, and each column contains only binary data.  

Imbalanced Data

input

imbalance

oversampling

undersampling

SMOTE: Synthetic Minority Oversampling Technique

cauation

The synthetical data have one direction, which might be noise rather than data.

ADASYN: Adaptive Synthetic Sampling Approach

SMOTE + Tomek Links

SMOTE + ENN

Objectives of Cross-Validations

To answer some questions about which part of the dataset should be training and testing data, we might shuffle the data and randomly split the dataset into training and testing. Moreover, which parameters are the best for this dataset? These two questions lead data scientists to create cv techniques.
 

A

C

B

D

Which spilts are the best for the assigned parameters? Depend right? Practically, we should avoid depend.

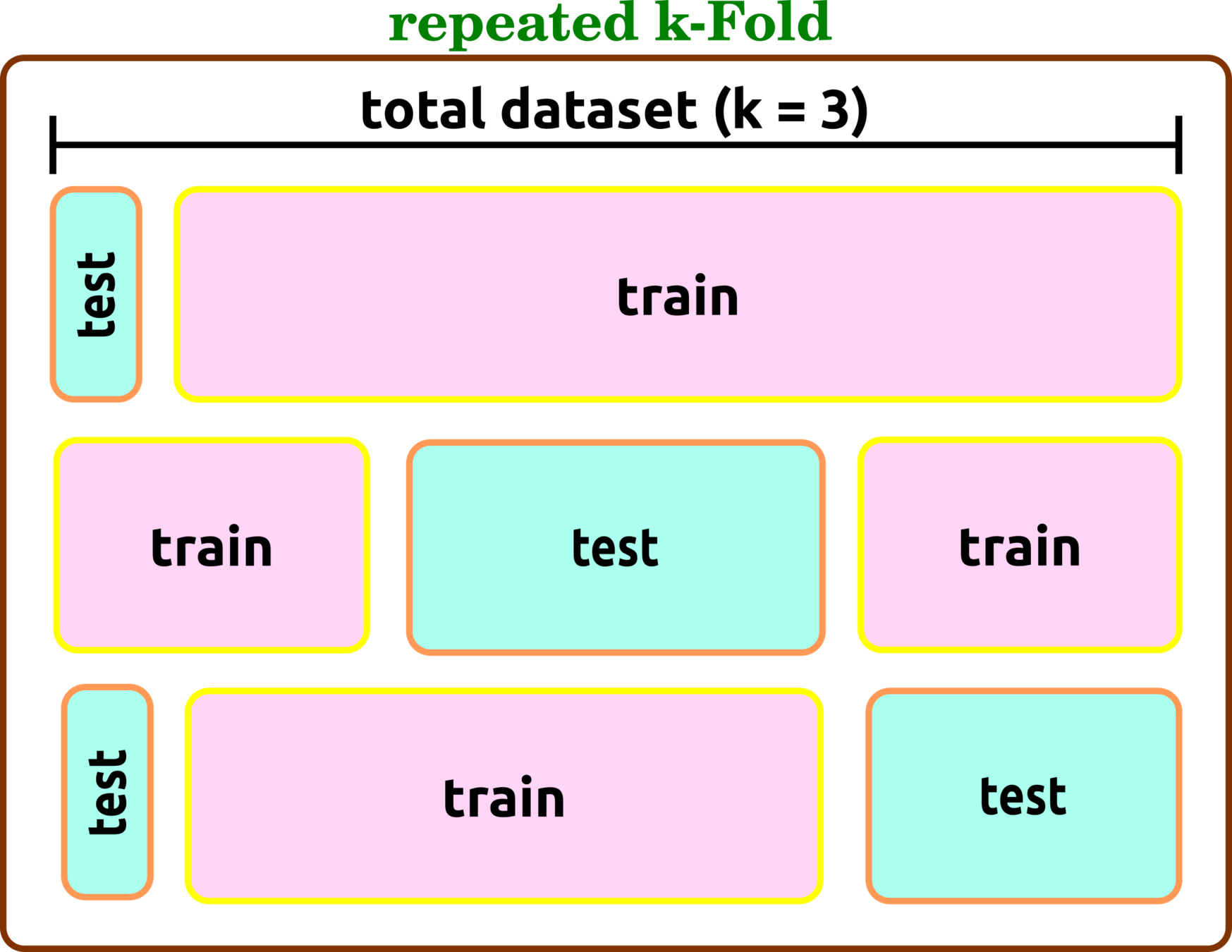
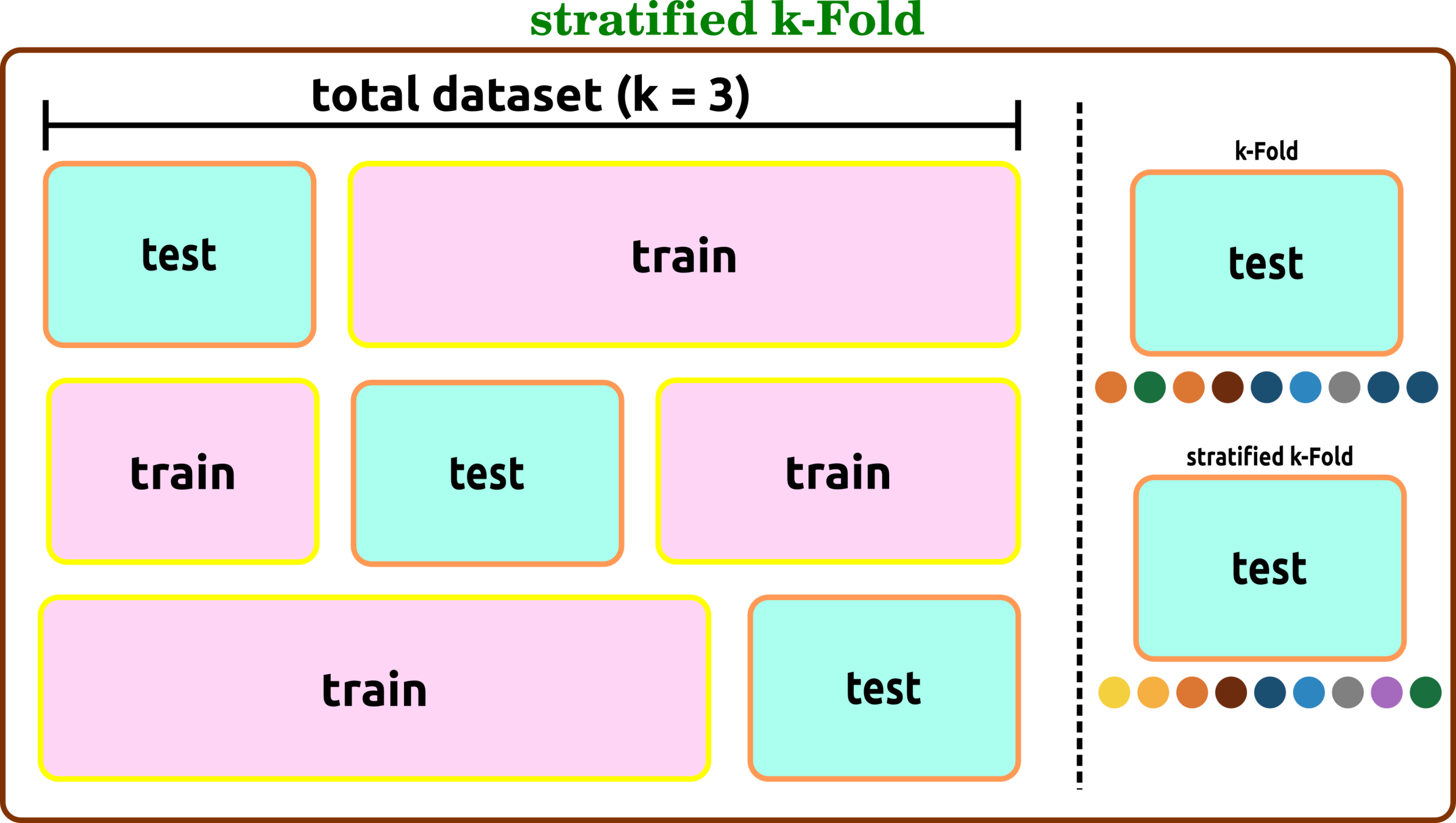
Cross-Validation Types

hold-out

the ratio of train and test is fixed 

k-Fold

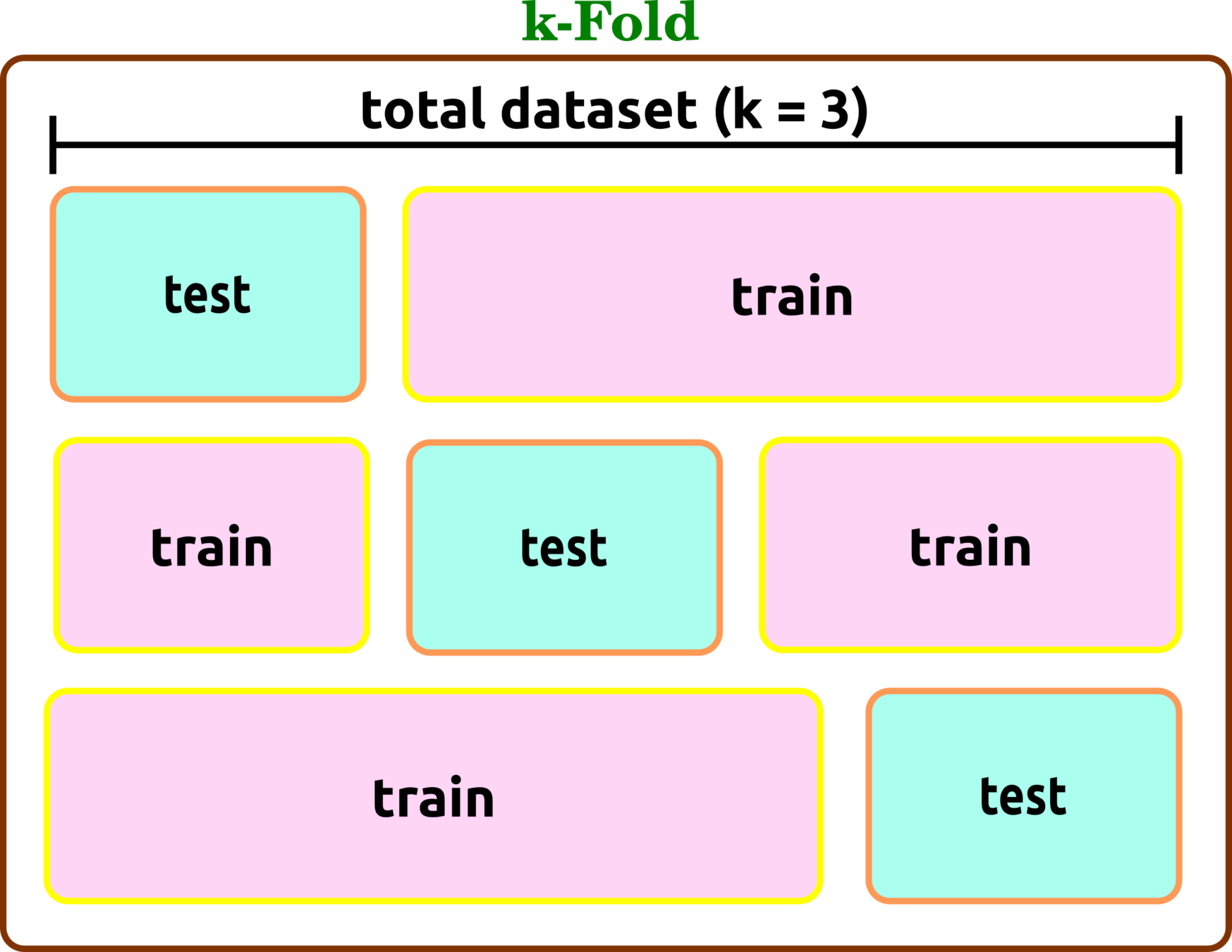
split a dataset into a number of groups (fold), so-called k, and then evaluate the model in each iteration.

repeated k-Fold

stratified k-Fold

similarly with k-Fold, except the size of test data can be varied

all of the tree cv types can combine with stratified technique when test data are sorted to have all labels before evaluation.

basic

CatBoost Multiclass Classification

input data
continued

feature engineering

normalization

outliers

missing value

encoding

input data
continued
feature engineering

CatBoost

default parameters

early stopping

over-fitting detection

model training

k-fold CV

Underfiting, Fit, and Overfitting

visualization

underfitting

fit???

overfitting

binary in-depth

FINAL EXAM GUIDELINE

The final presentation will hold on Jan 03, 2022, starting 9.00 - 12.00. Students must turn on the camera and present for 12 mins talk, 5 mins discussion.

Submit your final presentation by Jan 02 (11.00 p.m)

Guideline

1. Compare advantages and disadvantages among pipelines. Students might design different pipelines and describe why the selected pipeline can yield the best inference.

2. Explain your code

3. Select one preprocessing that is the most important (increase/decrease f1 score or error)

4. Suppose we would like to predict only one facies, which facies should we select. Please use scientific description to address a hypothesis.

5. Suppose a new frontier area contains high shaly sand zones, from this information, which well in our dataset should use for the training model. 

Questions

1. Please compare the pros and cons of applying normalization before the outlier removal. 

2. List the top 2 essential parameters and show some evidence.

3. Show how to count number of facies in each well.

5. What are the limitations of using inference to predict a frontier area?

6. The method in this project is supervised or unsupervised learning?

4. Which well should not use for testing? Why?

7. Imbalanced data should apply before or after outlier removers? Why?

8. Please use educational guest, which kind of well is the most importance?

9. If we would like to bargain the exploration cost of well logs, please design your experiment to create evidence that can convince the wireline company.

10. Please design the experiment to find some hydrocarbon saturation intervals (the current dataset has no saturation information).

CH 6: HYPERPAMETER TUNING

Hyperparameter Tuning

  • test all parameters
  • no need for previous information
  • exhausted search
  • skip some parameters
  • no need for previous information
  • faster search

grid search

random search

parameter a

parameter b

parameter a

parameter b

Grid Search with Cross-Validation

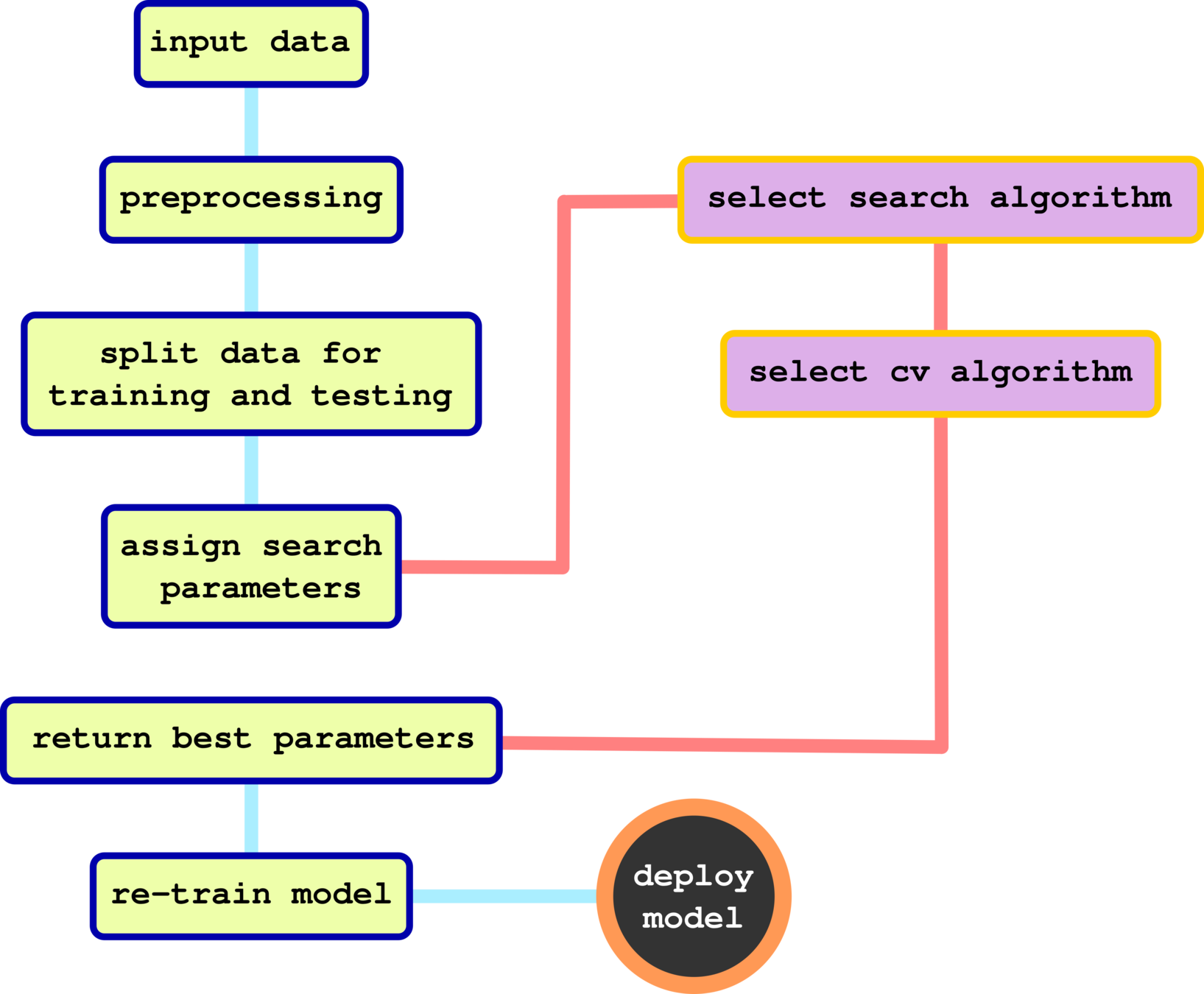
Hyperparameter Tuning (Baysian Search)

CH 7: GAUSSIAN PROCESS REGRESSION

xxx

Made with Slides.com