Funciones

Profesor: Santiago Quiñones

Docente Investigador

Departamento de Ingeniería Civil

Programación - Ingeniería Civil

Contenidos

Módulos existentes

Introducción a las funciones

Sintaxis, invocación, parámetros, retorno de valores

Problemas

Módulos existente

Existes muchas librerías o módulos ya programados (math, random)

Realizan todo tipo de tareas, simples o complejas

Mucho trabajo ya está hecho.

Revisar repositorio https://pypi.org

Primer método

Cómo importarlos

import <nombre modulo>

Ejemplo

import math

Segundo método

Cómo importarlos

from <nombre módulo> import <elemento1>, <elemento2>

Ejemplo

from math import pow, sqrt

Tercer método

Cómo importarlos

from <nombre módulo> import <elemento1> as <alias>

Ejemplo

from math import e as euler

Cuarto método

Cómo importarlos

from <nombre módulo> import *

Ejemplo

from math import *

Con el primer método

Cómo llamarlas

import modulo
modulo.funcion(argumentos)

Ejemplo

import math
math.sin(0)

Con el segundo y cuarto método

Cómo llamarlas

from modulo import funcion
funcion(argumentos)

Ejemplo

from random import uniform
uniform(0, 1)

Con el tercer método

Cómo llamarlas

from modulo import funcion as mifun
mifun(argumentos)

Ejemplo

from random import randint as rnd

rnd(5, 10)

Ejemplo completo

from random import randint as rnd
from math import pi, e

lanzamiento = rnd(1, 6)

if lanzamiento < 4:
  print(pi * lanzamiento)
else:
  print(e * lanzamiento)

Ejemplo completo

Introducción a las funciones

¿Por qué necesitamos funciones?

Ayuda a evitar la repetición de código y a mantenerlo organizado.

Facilita la corrección de errores al aislar el código en una función.

Permite navegar de manera más fácil en un algoritmo complejo

¿Por qué necesitamos funciones?

Imagina que tendrías que hacer si tu jefe te pide cambiar el mensaje para que fuese más cortés, por ejemplo que comience con la frase “Por favor”.

 

¿Es posible separar ese código repetido, darle un nombre y hacerlo reutilizable?

 

  • Fragmento de código que recibe parámetros, ejecuta acciones, y retorna un resultado. 

  • Puede ser entendidas igual que el ámbito matemático.

Funciones

f(x,y) = x^2 + y^2

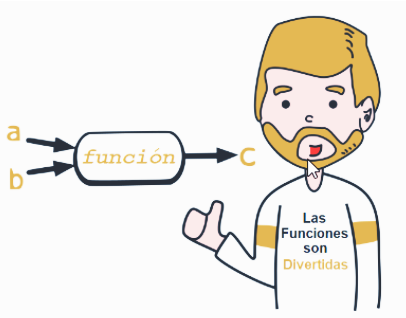
Sintaxis, invocación, parámetros y argumentos, retorno de valores

Sintaxis

  1. Siempre comienza con la palabra reservada def (definir)

  2. Después de def va el nombre de la función (sigue las mismas reglas para asignar nombres de variables)

  3. Espacio para un par de paréntesis.

  4. La línea termina con dos puntos

  5. La línea inmediata después de def marca el comienzo del cuerpo de la función.

Invocación de funciones

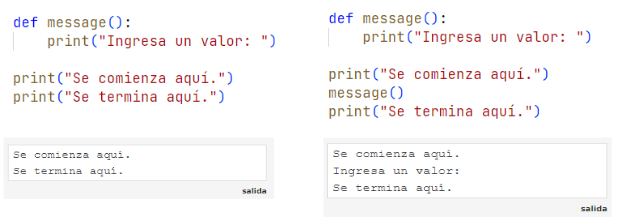
No se está utilizando la función, lee la definición de la función y la recuerda, pero no la ejecuta sin tu permiso.

En este segundo caso se ha insertado la invocación de la función entre los dos mensajes.

1

2

Invocación de funciones

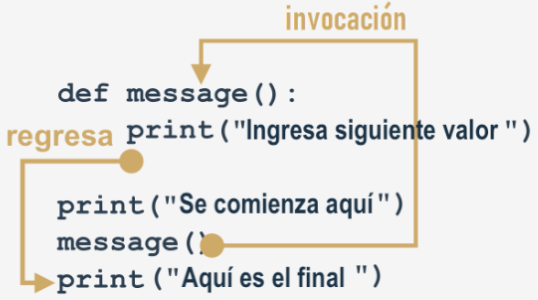
Invocación de funciones

Definición de función parametrizada

Una vez que nosotros definimos una función, podemos llamar de la siguiente manera

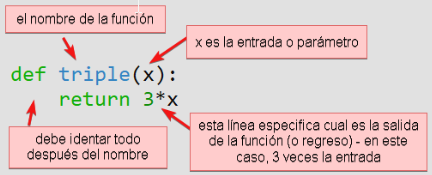
Definición de función parametrizada

Multiples líneas, multiples parámetros

Ejemplos de uso:

Multiples líneas, multiples parámetros

Problemas

¿Cuál es la salida del siguiente código?

A. 5

B. 9

C. 4

D. 3

E. 8

Reto 1: Calcular el IMC

Definamos una función que calcula el índice de Masa Corporal (IMC):

Como puedes observar, la fórmula ocupa dos valores:

  • peso (originalmente en kilogramos)
  • altura (originalmente en metros)

Reto 2: La longitud de segmento

Dados cuatro números reales que representan coordenadas cartesianas: (x1,y1),(x2,y2). Escribe una función distance(x1, y1, x2, y2) para calcular la distancia entre los puntos (x1,y1) y (x2,y2). Lee cuatro números reales e imprime la distancia resultante calculada por la función.

 

La fórmula de la distancia entre dos puntos se encuentra en Wolfram.

(x_1, y_1)
(x_2, y_2)

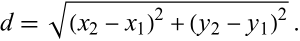
Reto 3: Tipo de triángulo

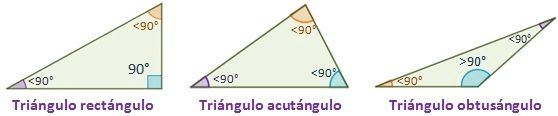
Según el teorema de Pitágoras el cuadrado de la hipotenusa es igual a la suma del cuadrado de los catetos: (C² = A² + B²). Utilizando este concepto es posible conocer de que tipo es un triángulo:

Si C²=A²+B² es un triángulo rectángulo.
Si C²<A²+B² es un triángulo acutángulo.
Si C²>A²+B² es un triángulo obtusángulo.

 

Escriba una función que reciba los dos catetos e hipotenusa y devuelva el tipo de triángulo. Realice pruebas manuales. 

 

Reto 4: Figuras geométricas

Generar una solución que implemente 3 funciones. Que permitan calcular el área de un cuadrado, área de un triángulo y área de un rectángulo. Cada función debe recibir los datos necesarios y devolver el valor correspondiente. Invoque a las funciones con la información necesaria y valide los resultados de forma manual. 

  • El área del cuadrado es igual a lado x lado
  • El área del triángulo es igual a (base x altura)/2
  • El área del rectángulo es igual a base x altura