Gewinnt immer die Bank?

Strategische Mathematik oder doch nur einfaches Glück?

Aufbau vom europäischen Roulette:

Zahlen 1 bis 36 in Farben rot und schwarz
Zahl 0 (en Prison) grün

Verschiedene Spiele:

Rouge/Noir (Gewinn 2x Einsatz)
Pair/Impair (Gewinn 2x Einsatz)
Manque/Passe (Gewinn 2x Einsatz)
einfaches Farbenspiel (Gewinn 36x Einsatz)

Wie rechne ich mir den durchschnittlichen Verlust bzw. Gewinn pro Spiel aus?

Mit dem Erwartungswert:

=die Summe aller möglichen Ereignisse multipliziert mit deren Wahrscheinlichkeit

z.B: E(x)= \frac {2}{5} * 1 + \frac {3}{5} * (-1) = \frac {-1}{5} = -0,20

Verlust von 20c pro Spiel bei 1-4

Macht es einen Unterschied immer auf "Gerade" oder "Ungerade" zu setzen?

Nein, da "Gerade" die gleiche Wahrscheinlichkeit besitzt wie "Ungerade".

Arithmetische Progress

eine Zahlenfolge

4, 9, 14, ... 29, 34,...

5, 11, 17, 23, ..., 35, 41, ...

7, 20, 33, 46, ..., 72, 85, ...

50,33,16, ..., -35, -52, ...

Ausgangssituation

nach jedem Spiel setzten wir um einen Euro mehr
wir starten mit einem Euro

B... Budget

n... Anzahl der Spiele

Beispiel:

x = 8

Formel:

x = \frac {n*(n+1)} {2}

Herleitung:

1,2,3,4, ... (n-3),(n-2),(n-1), n

Mitte

\frac {n}{2}

n+1

\color {red} \frac {n}{2}

\color {limegreen} (n+1)

Die Martingalestrategie

Die Martingalstrategie verdoppelt den Einsatz nach jeder verlorenen Wette, um mit dem ersten Gewinn alle Verluste auszugleichen.

Gewinnchancen

Mit unbegrenztem Kapital führt die Martingalstrategie sicher zum Gewinn

die Gewinnchance beträgt dann 100 %.

Warum?

Beispielsweise verlieren wir 4 Runden und gewinnen die 5-te

1+2+4+8+16 16 gewonnen

15 verloren

1 Euro Profit

Die Formel zur Ausrechnung des verbrauchten Budgets, um $n$ -mal zu spielen, ist:

$Bn=E0⋅(2n−1)B_n = E_0 \cdot (2^n - 1)$

$En=E0⋅2n−1E_n = E_0 \cdot 2^{n-1$

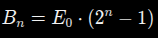
Die Formel zur Ausrechnung, wie viel wir für das n-te Spiel brauchen, ist:

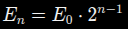
Formeln

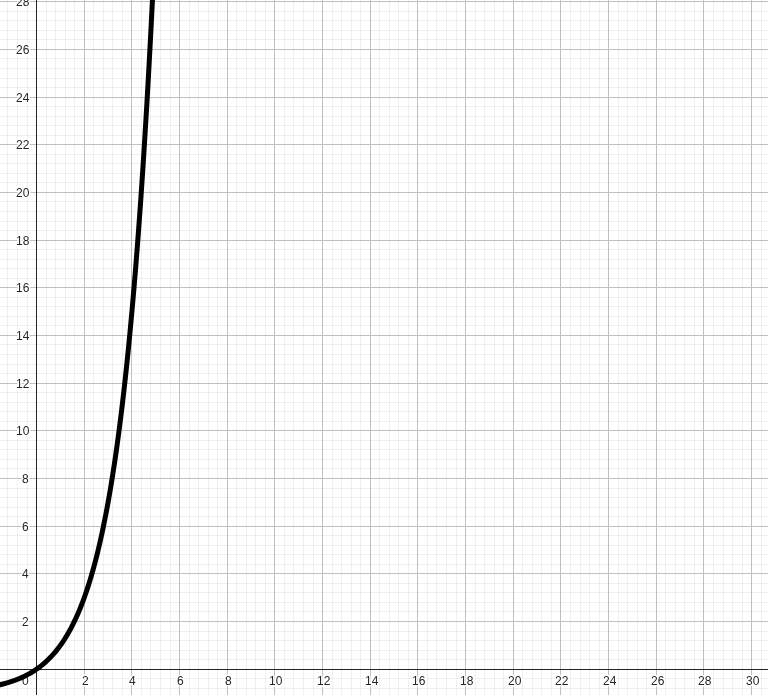
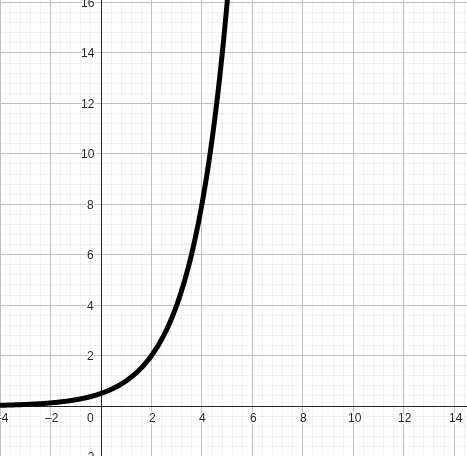
Abgewandelte Martingalstrategie

Der Einsatz wird nach jeder Runde verdreifacht

2 3

Gesamter Einsatz = [(3^n)-1]/(3-1)

Einsatz wird nach jeder Runde mit k multipliziert

2 b

Gesamter Einsatz =

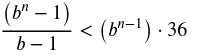
Runden n	1	2	3	4	5
Einsatz in Runde	1	4	16	64	256
Gesamter Einsatz	1	5	21	85	341
Möglicher Gewinn	2	8	32	128	512

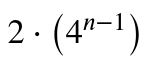
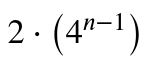
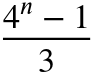
Beispiel: k=4

Das Setzen auf Zahlen

Anstatt des Pair/Impair-Spiels kann man auch auf eine beliebige Zahl setzen z.B.: 1

Gewinn = 36*Einsatz

Um den selben Effekt wie bei der Martingalstrategie zu erzielen muss der Einsatz nicht mehr verdoppelt werden

Bisheriger gesamter Einsatz < Möglicher Gewinn diese Runde

Bisheriger Einsatz

Möglicher Gewinn

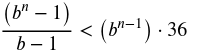
Der Einsatz muss nur mehr mit 1.02857 multipliziert werden, um einen Gewinn erwarten zu können

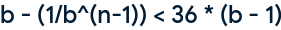
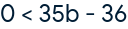
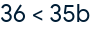
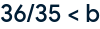
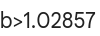
En Prison Regel

Wird die Zahl 0 gerollt, gilt der Einsatz als En Prison. Das bedeutet, dass erneut gedreht wird. Trifft das gesetzte Ereignis jetzt ein so erhält man den Einsatzt nur einfach zurück.

Das faire Roulette

In diesem fairen Roulette wird nur die Null entfernt. Dadurch haben Bank und Spieler die selben Gewinnchancen.

Statt 18/37 1/2

Weitere Setzstrategien

Setzen des gesammten bisherigen Einsatzes

Bei dieser Strategie erwartet man keinen Gewinn, aber eine 0 am Ende

Verhundertfachen des letzten Einsatzes

Bei dieser Strategie gibt es wieder die Möglichkeit einen Gewinn zu erwarten

Bisheriger gesammter Einsatz = Möglicher Gewinn diese Runde

Bisheriger gesammter Einsatz < Möglicher Gewinn diese Runde

SPORTWETTEN

„Sportwetten sind Glücksspiele, bei denen man

Geld auf den Ausgang von Sportereignissen setzt.

Dabei besteht immer das Risiko, Geld zu verlieren.“

SUREBETS/ARBITRAGE

geschicktes Setzen auf alle möglichen Ausgänge eines Sportereignisses bei verschiedenen Buchmachern

Typische Quoten

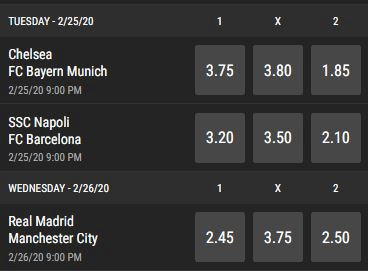
SUREBET berechnen

(1/Quote 1)+(1/Quote 2)+...<1

Ist die Summe kleiner als 1, so liegt eine Surebet vor

EINSÄTZE berechnen

$(1/ Surebet)*(Gesamteinsatz / jew. Quote)$

Gesamteinsatz = gesamtes Budget, welches auf die verschiedenen Quoten gesetzt wird

BEISPIEL

Quote

A: 8,00

B: 5,30

C: 1,50

Einsatz: 100€

$(1/ 8,00)+(1/ 5,30)+(1/ 1,50)= 0,981$

Da 0,981<1, ist es eine funktionierende Surebet

EINSÄTZE

$A:(1/ 0,981)*(100/ 8,00) \approx 12, 75€$

$B:(1/ 0,981)*(100/ 5,30) \approx 19,25€$

$C:(1/ 0,981)*(100/ 1,50) \approx 68,00€$

Mit einem Budget von 100€ und folgenden Einsätzen kann ohne Verlust gewettet werden.

SANKT PETERSBURG PARADOX

Text

berühmtes mathematisches Gedankenexperiment

Spiel:

Es wird eine Münze so lange geworfen, bis zum ersten Mal „Zahl“ erscheint.

Bei erstem Erscheinen von „Zahl“ im $k$ -ten Wurf erhält der Spieler den dazugehörigen Gewinn.

1,2,4,8,16,32,64

1 2 3 4 5 6

Gewinn

Anzahl der würfe

Mathematisches Modell

Für den k-ten Münzwurf

$G = 2^k$

$P = (1/2)^k$

Warscheinlichkeit

Gewinn

Erwartung vom Paradox

$E(X) = \sum (1/2)^k * 2^k =$

$\infty$

$k=1$

Gewinn(G)

Warscheinlichkeit(P)

$\infty$

Trotz undendlichem Erwartungswert würde keiner viel Geld dafür bezahlen.

Gibt es noch Fragen?

Gewinnt immer die Bank?

Strategische Mathematik oder doch nur einfaches Glück?

Aufbau vom europäischen Roulette:

Verschiedene Spiele:

Wie rechne ich mir den durchschnittlichen Verlust bzw. Gewinn pro Spiel aus?

Mit dem Erwartungswert:

Arithmetische Progress

eine Zahlenfolge

Ausgangssituation

Beispiel:

Formel:

Herleitung:

Die Martingalestrategie

Gewinnchancen

Warum?

Formeln

Beispiel: k=4

Weitere Setzstrategien

SPORTWETTEN

SUREBETS/ARBITRAGE

SUREBET berechnen

EINSÄTZE berechnen

(1/Surebet)*(Gesamteinsatz/jew. Quote)

BEISPIEL

(1/8,00)+(1/5,30)+(1/1,50)=0,981

EINSÄTZE

A:(1/0,981)*(100/8,00)≈12,75€

B:(1/0,981)*(100/5,30)≈19,25€

C:(1/0,981)*(100/1,50)≈68,00€

SANKT PETERSBURG PARADOX

Spiel:

1,2,4,8,16,32,64

Mathematisches Modell

G=2^k

P=(1/2)^k

E(X)=∑(1/2)^k*2^k=

∞

k=1

∞

$(1/ Surebet)*(Gesamteinsatz / jew. Quote)$

$(1/ 8,00)+(1/ 5,30)+(1/ 1,50)= 0,981$

$A:(1/ 0,981)*(100/ 8,00) \approx 12, 75€$

$B:(1/ 0,981)*(100/ 5,30) \approx 19,25€$

$C:(1/ 0,981)*(100/ 1,50) \approx 68,00€$

$G = 2^k$

$P = (1/2)^k$

$E(X) = \sum (1/2)^k * 2^k =$

$\infty$

$k=1$

$\infty$