Numbers and Logic

https://slides.com/djjr/numbers-and-logic

What you will need today

  • Pencil and Paper
  • Slides open in a second window/tab

Outline

  1. Numbers Basics
    1. Decimal to Binary
    2. Binary to Decimal
    3. Binary to Hexadecimal
    4. Binary coded decimal

  2. Encoding

    1. ASCII translation

    2. URL encoding

  3. Language and logic

    1. Everyday language to logical expression

    2. Logical expression to everyday language

  4. Logic and Circuits

    1. AND, OR, NOT

    2. Simple expressions and circuits

  5. Seven segment display

    1. For what decimal digits is segment A, etc. illuminated?

    2. BCD version of inputs as W,X,Y,Z

    3. Expression for segment A

    4. What would would circuit for A look like

    5. Is there a simpler circuit

    6. Simplifying an expression  by hand

    7. Simplifying an expression with KMap

Half Adder

Can we build a circuit that can add two numbers together?

7-Segment Driver

Can we build a circuit that will translate a binary number into signals that can drive a physical display?

Two Tasks

Numbers Basics

  • Decimal to Binary
  • Binary to Decimal
  • Binary to Hexadecimal
  • Binary coded decimal

Preparation

  1. Filho. 2017. Computer Science Distilled, p 165
  2. Eames Labs. 1977. Powers of Ten (10m16s)
  3. Sample from among
  4. Khan Academy. 2014. "Adding in Binary" (2m47s)

Eames Lab: Powers of Ten

MathCrazyTutoring (2007 - 1m35s)

Khan Academy. 2011. "Binary Numbers" (10m33s)

Khan Academy. 2014. "Introduction to number systems and binary" (9m59s)

Cope (2017), Binary Numbers Explained (14m25s)

Khan Academy. 2014. "Adding in Binary" (2m47s)

Exercises

Binary = Base 2

Positional Number Systems

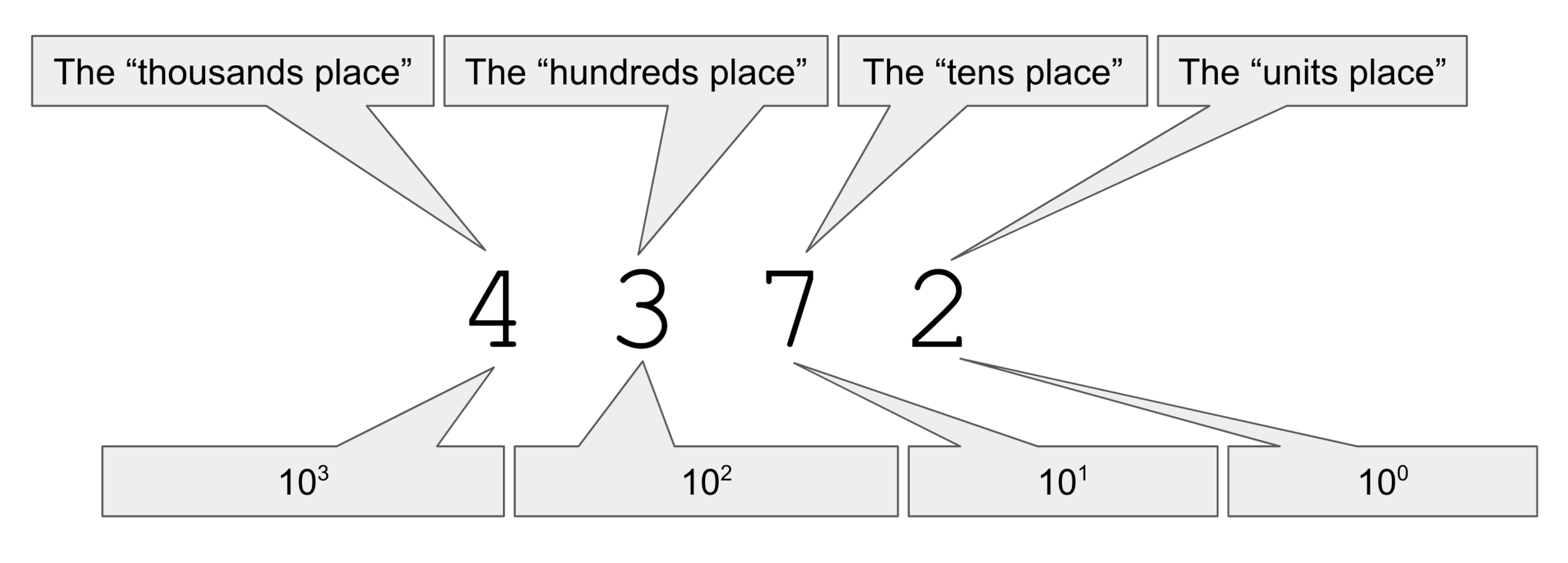
Positional Number Systems

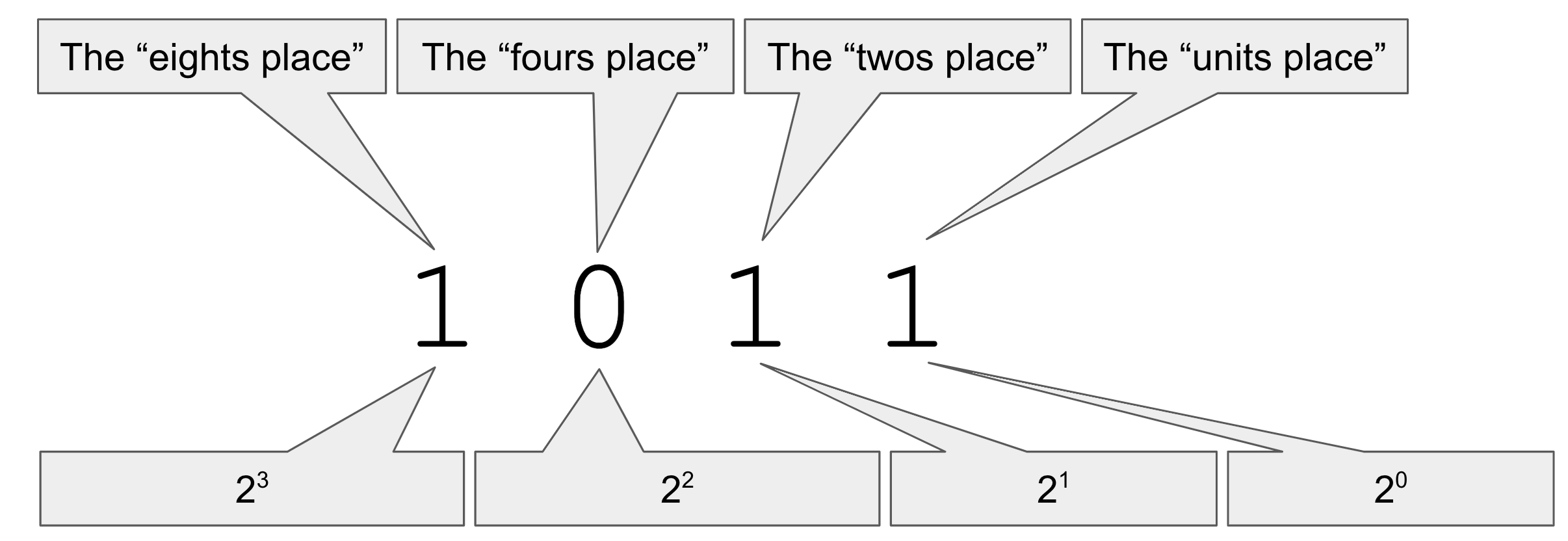
Positional Number Systems

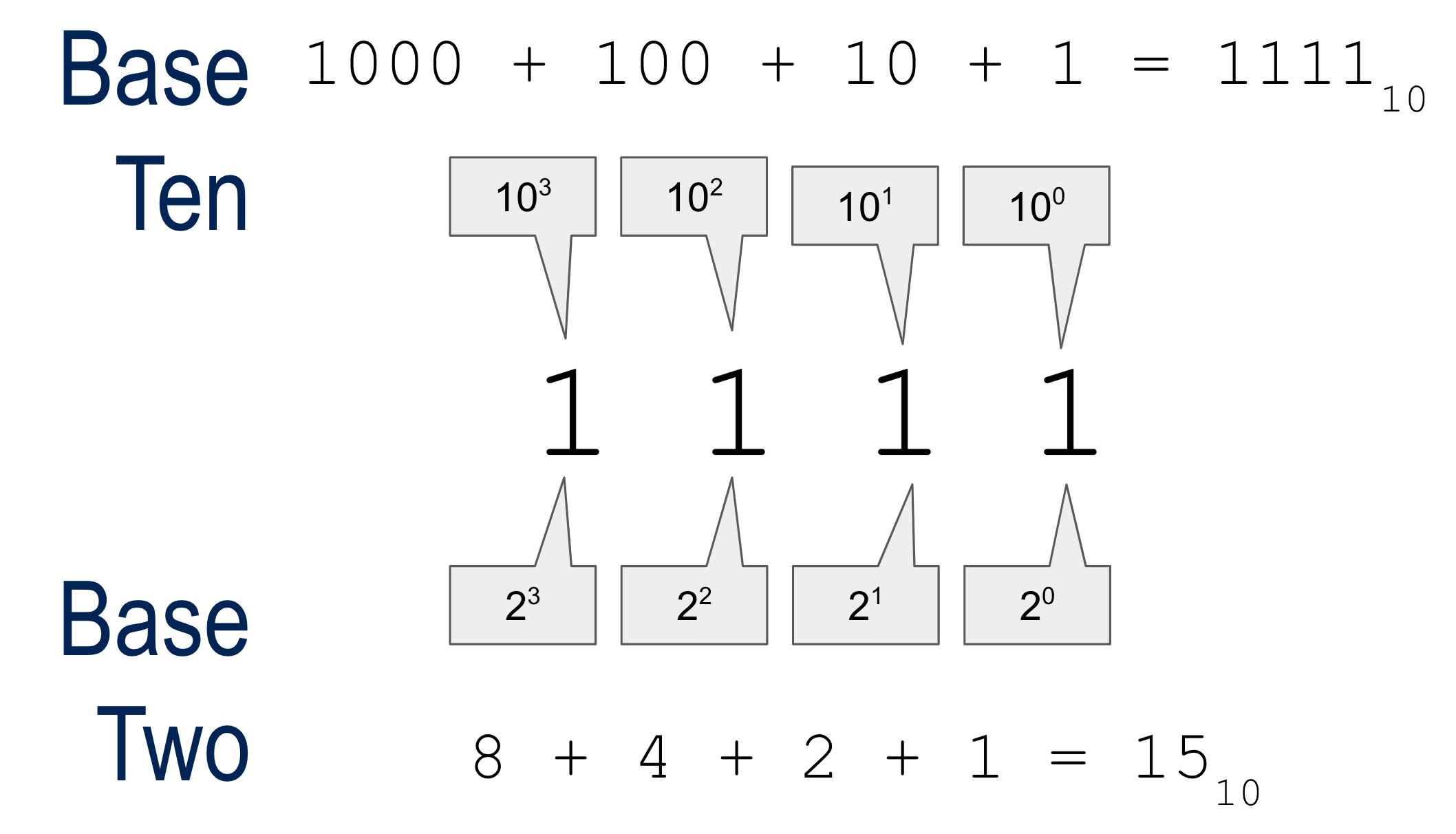
STOP+THINK

 

  Write out
  first ten

  binary numbers

STOP+THINK

 

  Write out   first ten binary numbers

0, 1, 10, 11, 100, 101, 110,
111, 1000, 1001, 1010

Binary 0 - 15

0000   0100   1000   1100
0001   0101   1001   1101
0010   0110   1010   1110
0011   0111   1011   1111

 

HEXADECIMAL 0 - 15

0   4   8   C
1   5   9   D
2   6   A   E
3   7   B   F

 

HEXADECIMAL AS BINARY SHORTHAND

1011010101010111101010101010

1011 0101 0101 0111 1010 1010 1010

B 5 5 7 A A A

ENCODING

ASCII

American Standard Code for Information Interchange

  • Numerical code for letters, digits, symbols
  •  

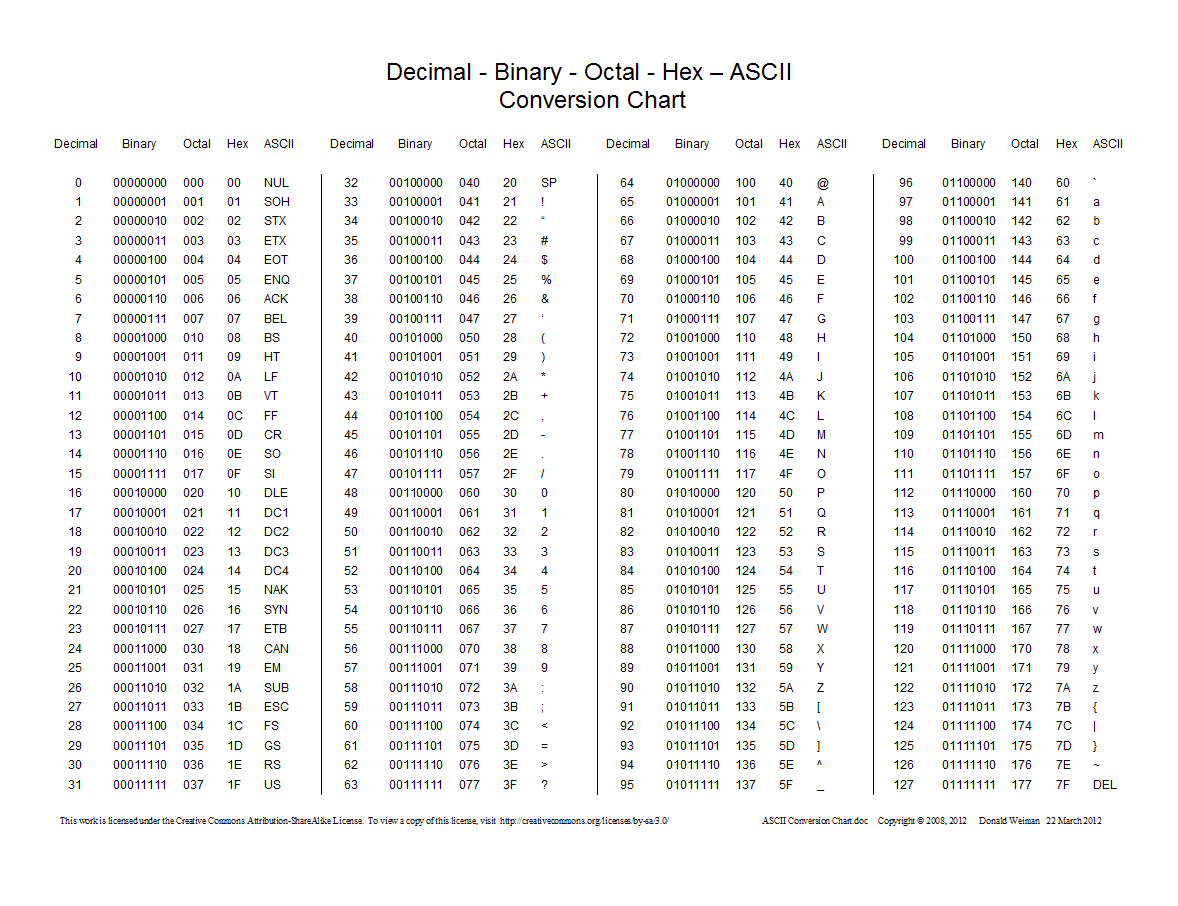
Other Notations

0b11010100

0xD4

Language and logic

  • Everyday language to logical expression

  • Logical expression to everyday language

LOGICAL VALUES

TRUE = 1

FALSE = 0

LOGICAL VARIABLES

  • A, B, C, ...
  • Can stand for anything that can be true or false
  • Including logical expressions
    • e.g., A = B + C
  • "A is the statement that either B or C is true"

LOGICAL OPERATORS

  • "Binary" Operators (connecting two values)
    • AND
    • OR
  • "Unary" Operator
    • NOT

LOGICAL OPERATORS

  • A and B
    • also written AB, A∧B, A·B
  • A or B
    • also written A+B, A∨B
  • not A
    • also written ~A, !A, ¬A, Ā

LOGICAL OPERATORS

  • W=AB
    • True if both A, B true
  • W=A+B
    • True if either or both A,B true
  • W=!A
    • True if A is false, false if A is true

TRUTH TABLES

A logical expression is DEFINED by its truth table which shows its value for every possible combination of inputs

TRUTH TABLES

A B A+B
1 1 1
1 0 1
0 1 1
0 0 0

row for each

input combination

row for each

input combination

column
for each

variable

column
for "output"

A B C !A!B + BC

Build Truth Table for !A!B + BC

A B C !A!B + BC
1 1 1
1 1 0
1 0 1
1 0 0
0 1 1
0 1 0
0 0 1
0 0 0

Build Truth Table for !A!B + BC

1

A B C !A!B + BC
1 1 1 1
1 1 0
1 0 1
1 0 0
0 1 1 1
0 1 0
0 0 1 1
0 0 0 1

Build Truth Table for !A!B + BC

1

2

3

A B C !A!B + BC
1 1 1 1 1
1 1 0
1 0 1
1 0 0
0 1 1 1 1
0 1 0
0 0 1 1 1
0 0 0 1 1

Build Truth Table for !A!B + BC

1

2

3

4

 TRY: (A & B) v (~A & ~B)

Pause

Logic and Circuits

  • logical values and electricity

  • AND, OR

  • Basic Logic Gates

  • Simple expressions and circuits

Logical Values + Electricity

+5 volts

0 volts

1

0

true

false

Logical Values + Electricity

+5 volts

+5 volts

logical 0

logical 1

AND, OR

Logic Gates

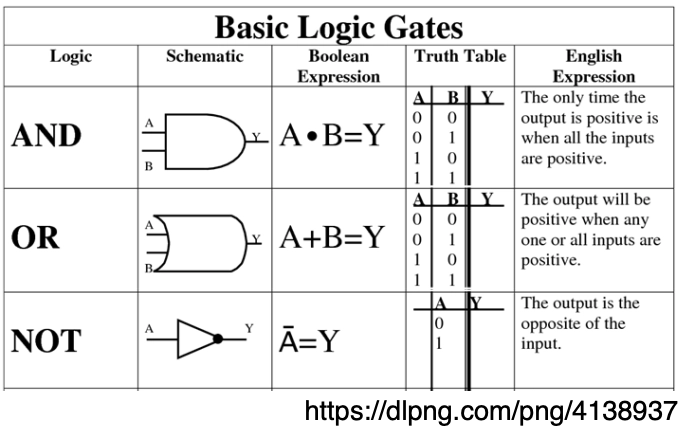
Simple expressions + circuits

AB + BC

A

B

C

Simple expressions + circuits

A+B+C

A

B

C

Simple expressions + circuits

A
 

B
 

C

!A!B + BC

!A

!B

B

BC

!A!B

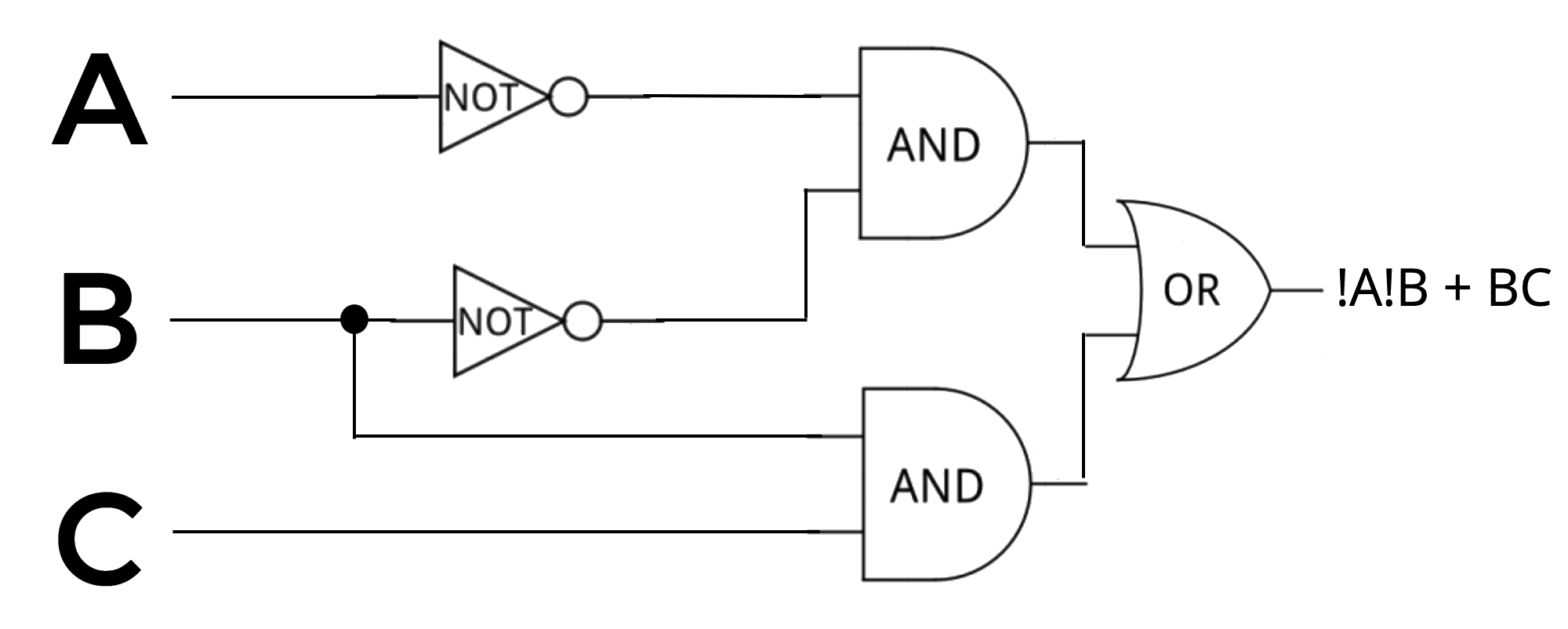
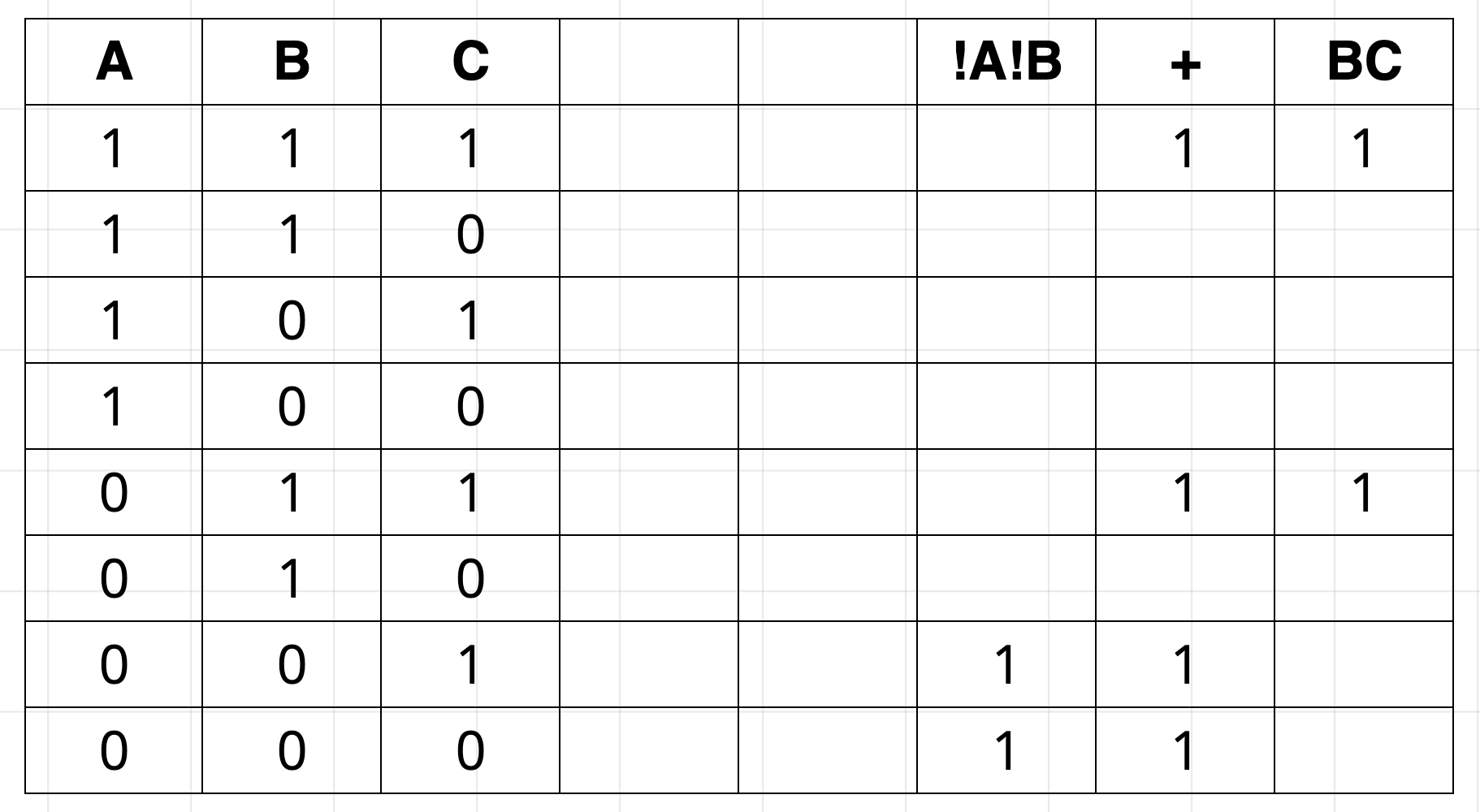
Pause

BINARY ARITHMETIC

  • ADDING SINGLE BITS TOGETHER
  • THE CARRY BIT
  • TRUTH TABLE

Binary
Arithmetic

 1
+1
10

Arithmetic in Binary

0 + 0 = 0

0 + 1 = 1

1 + 1 = 10

10 + 1 = 11

10 + 10 = 100

STOP+THINK 

 101
+100

 

 1111
+1010

 

 1100
+1010

 

STOP+THINK 

1
 101
+100
1001
111 
 1111
+1010
11001
 

1
 1100
+1010
10110

STOP+THINK
Could we write
numbers
with Donuts?

STOP+THINK
Could we do math
with Donuts?

Binary
Arithmetic

 1
+0
01

 0
+1
01

 0
+0
00

 1
+1
10

Binary
Arithmetic

 1
+0
01

 0
+1
01

 0
+0
00

 1
+1
10

  A
 +B
 WX

BinaryArithmetic

 1
+0
01

 0
+1
01

 0
+0
00

 1
+1
10

  A
 +B
 WX
A + B = W Z
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

BinaryArithmetic

 1
+0
01

 0
+1
01

 0
+0
00

 1
+1
10

  A
 +B
 WX
A + B = W Z
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

looks like
A and B

BinaryArithmetic

A + B = W Z
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

looks like
A and B

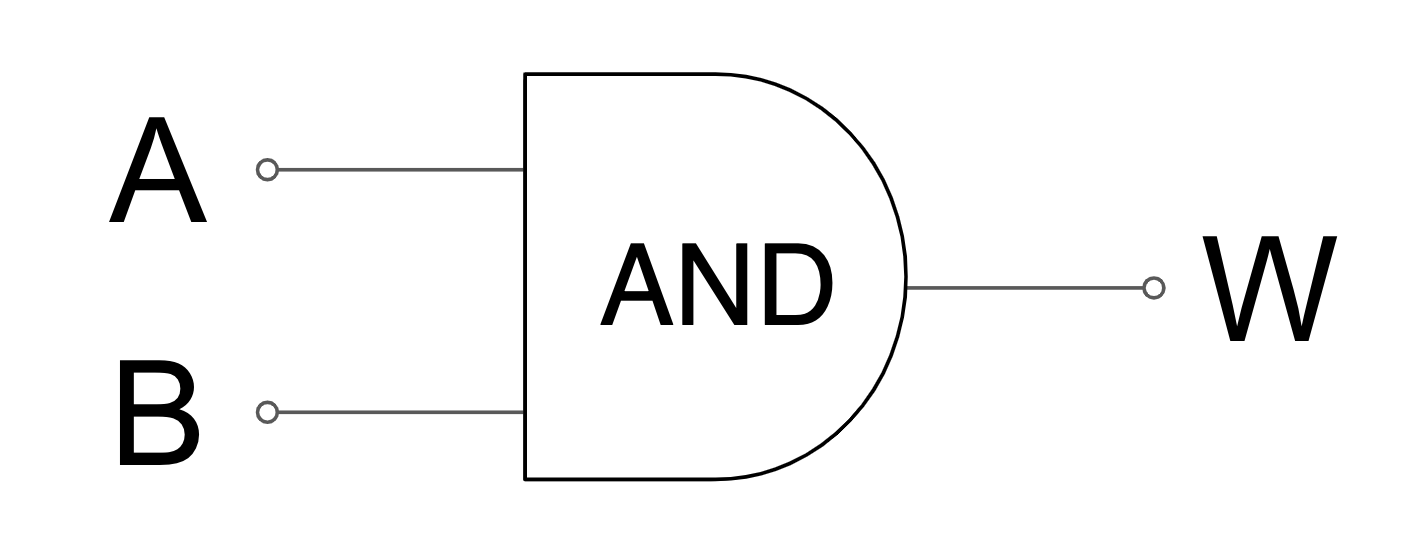
BinaryArithmetic

 1
+0
01

 0
+1
01

 0
+0
00

 1
+1
10

  A
 +B
 WX
A + B = W Z
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

looks like
A XOR B

BinaryArithmetic

A + B = W Z
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0

looks like
A XOR B

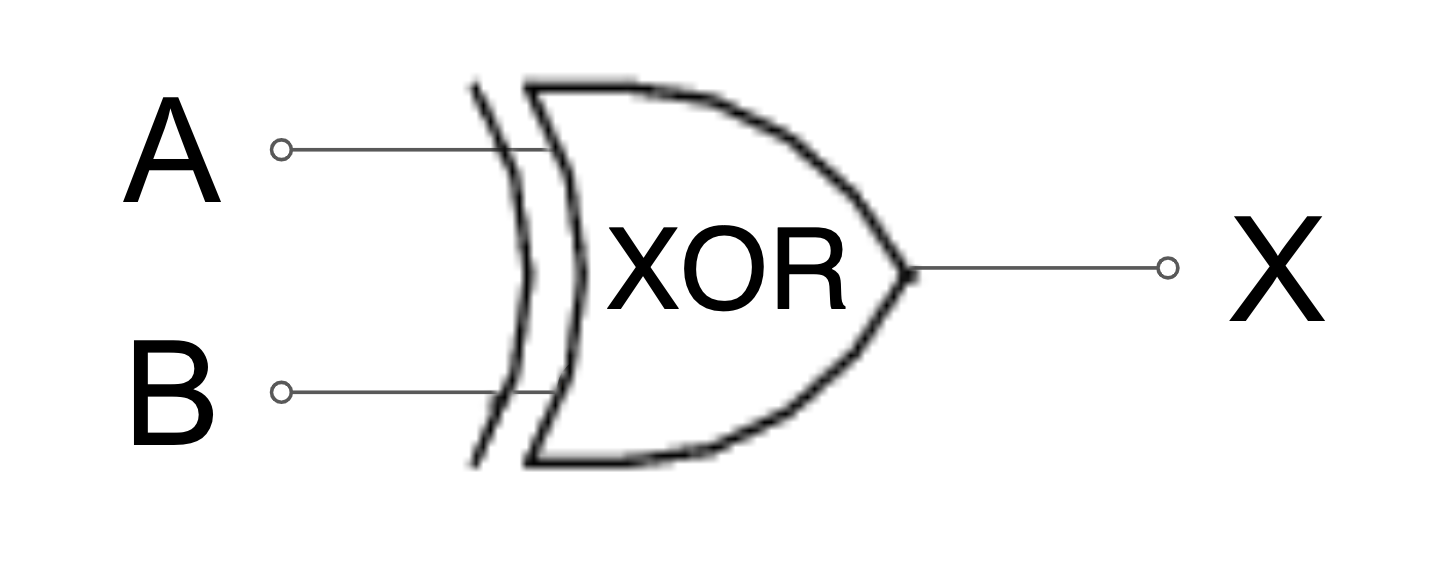
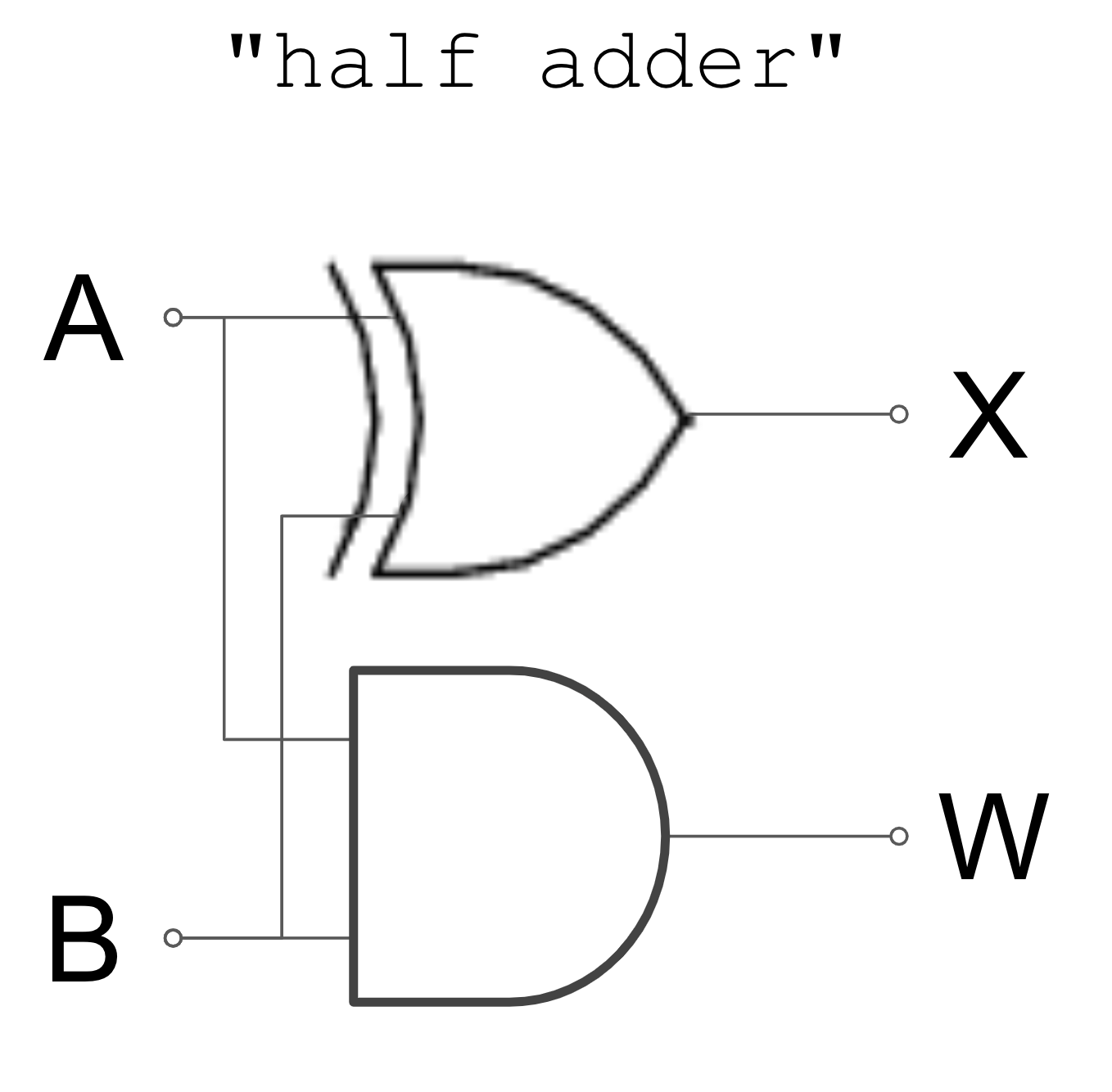
STOP+TRY: build the half adder circuit. Use switches for inputs and bulbs for outputs.

What
about
this?

ab
+cd
wxy

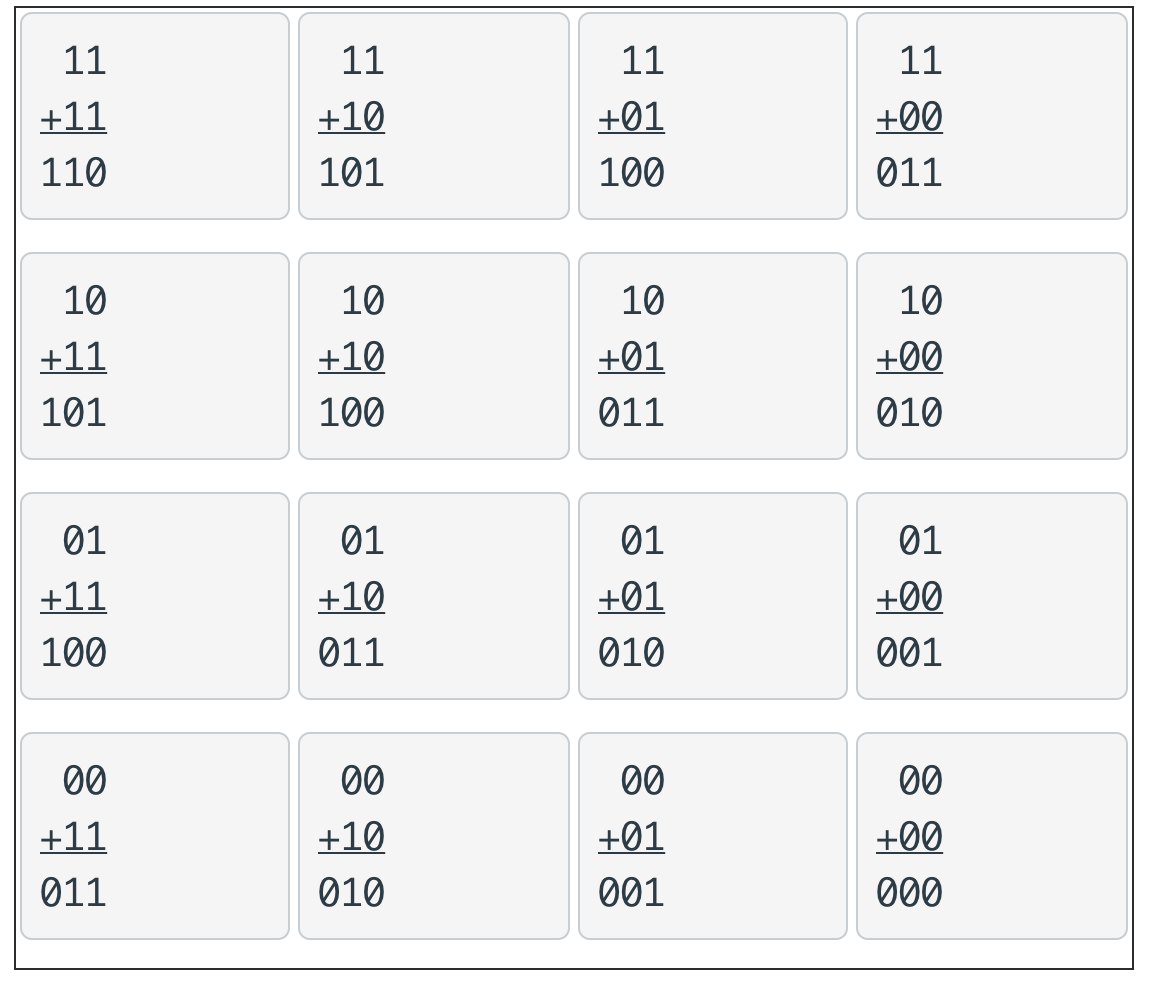
STOP+THINK
What would the truth table look like?

ab
+cd
wxy

ab
+cd
wxy

A B C D W X Y
1 1 1 1 1 1 0
1 1 1
1 1 1
1 1
1 1 1
1 1
1 1
1
0 1 1 1
0 1 1
0 1 1
0 1
0 1 1
0 1
0 1
0

11

+11

110

A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 0 1
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0
A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 0 1
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0

When is W true?

ABCD

or

ABC!D

or

AB!CD

or

A!BCD

or

A!BC!D

or

!ABCD

 

A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 0 1
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0

W=ABCD+ABC!D+AB!CD+A!BCD+!ABCD+A!BC!D

We could just build this as a circuit but it would be...complicated.

A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 0 1
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0

W=ABCD+ABC!D+AB!CD+A!BCD+!ABCD

We wonder if there is a simpler but equivalent version of this expression.

A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 0 1
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0

W=ABCD+ABC!D+AB!CD+A!BCD+!ABCD

Equivalent means it would have the same truth table.

A B C D W X Y
1 1 1 1 1 1 0
1 1 1 0 1 0 1
1 1 0 1 1 0 0
1 1 0 0 0 1 1
1 0 1 1 1 0 1
1 0 1 0 1 0 0
1 0 0 1 0 1 1
1 0 0 0 0 0 1
0 1 1 1 1 0 0
0 1 1 0 0 1 1
0 1 0 1 0 1 0
0 1 0 0 0 0 1
0 0 1 1 0 1 1
0 0 1 0 0 1 0
0 0 0 1 0 0 1
0 0 0 0 0 0 0

W=ABCD+ABC!D+AB!CD+A!BCD+!ABCD

Simpler means fewer terms and fewer operators.

e.g.

P=ABCD + ABC!D + AB!C + A!B

P=ABC(D+!D) + AB!C + A!B 

P=ABC(TRUE) + AB!C + A!B 

P=ABC + AB!C + A!B 

P=AB(C+!C) + A!B 

P=AB + A!B 

P=A(B+!B)

P=A 

A B C D ABCD ABC!D AB!C A!B P
1 1 1 1 1 1
1 1 1 0 1 1
1 1 0 1 1 1
1 1 0 0 1 1
1 0 1 1 1 1
1 0 1 0 1 1
1 0 0 1 1 1
1 0 0 0 1 1
0 1 1 1
0 1 1 0
0 1 0 1
0 1 0 0
0 0 1 1
0 0 1 0
0 0 0 1
0 0 0 0

Pause

Logic Reduction

AB + A!B = A(B+!B) = A and TRUE = A

 

A may be a compound expression

PQR + PQ!R = (PQ)(R+!R) = PQ

P=ABCD + ABC!D + AB!C + A!B

ABC(D+!D)

ABC

AB(C+!C)

ABC

ABC

AB

A(B+!B) 

A

CD
00 01 11 10
AB 00 !A!B!C!D !A!B!CD !A!BCD !A!BC!D
01 !AB!C!D !AB!CD !ABCD !ABC!D
11 AB!C!D AB!CD ABCD ABC!D
10 A!B!C!D ​A!B!CD ​A!BCD ​A!BC!D

Karnaugh Map

CD
00 01 11 10
AB 00 !A!B!C!D
0		 !A!B!CD1 !A!BCD
3		 !A!BC!D
2
01 !AB!C!D
4		 !AB!CD
5		 !ABCD
7		 !ABC!D
6
11 AB!C!D
12		 AB!CD
13		 ABCD
15		 ABC!D
14
10 A!B!C!D
8		 ​A!B!CD
9		 ​A!BCD
11		 ​A!BC!D
10

Karnaugh Map

CD
00 01 11 10
AB 00
 
 
 
01
 
 
 
 
11 AB!C!D
1		 AB!CD
1		 ABCD
1		 ABC!D
1
10 A!B!C!D
1		 ​A!B!CD
1		 ​A!BCD
1		 ​A!BC!D
1

P=ABCD + ABC!D + AB!C + A!B

CD
00 01 11 10
AB 00





01







11
 		 1 1 1 1
10
 		 1 1 1 1

P=ABCD + ABC!D + AB!C + A!B

P=ABCD + ABC!D + AB!CD + AB!C!D + A!BCD + A!BC!D + A!B!CD + A!B!C!D

NOTE: X1=B, X3=A, X0=C, X2=D

C is 1 here

D is 1 here

A is 1 here

B is 1 here

Finis

Encoding

  • ASCII translation

  • URL encoding

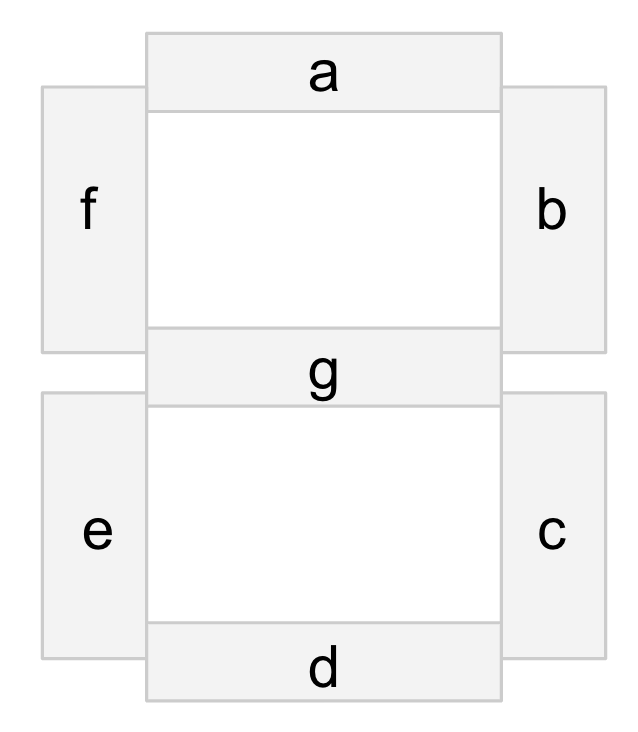
Seven segment display

  • For what decimal digits is segment A, etc. illuminated?
  • BCD version of inputs as W,X,Y,Z
  • Expression for segment A
  • What would would circuit for A look like
  • Is there a simpler circuit
  • Simplifying an expression  by hand
  • Simplifying an expression with KMap

Summary

  • Logic and Circuits

    1. AND, OR, NOT

    2. Simple expressions and circuits

  • Seven segment display

    1. For what decimal digits is segment A, etc. illuminated?

    2. BCD version of inputs as W,X,Y,Z

    3. Expression for segment A

    4. What would would circuit for A look like

    5. Is there a simpler circuit

    6. Simplifying an expression  by hand

    7. Simplifying an expression with KMap