NUMBERS

Numbers

  1. Filho. 2017. Computer Science Distilled, p 165
  2. Eames Labs. 1977. Powers of Ten (10m16s)
  3. Sample from among
  4. Khan Academy. 2014. "Adding in Binary" (2m47s)

Part 1: Intro

Part 2: Practice

Materials and Handouts

What You Need to Know

  1. CL01 Binary: Concept of base 2; notation; count to 10; dec2bin, bin2dec; first 10 powers of 2; binary arithmetic

  2. CL02 Hexadecimal: Concept of base 16; notation; hex2bin, bin2hex, hex2dec; ASCII encoding; URL encoding; HTML color encoding

  3. CL03 Counting by Powers: exponents, graphing, logarithms

hex2bin

bin2hex

Numbers Basics

  • Decimal to Binary
  • Binary to Decimal
  • Binary to Hexadecimal
  • Binary coded decimal

Binary = Base 2

Positional Number Systems

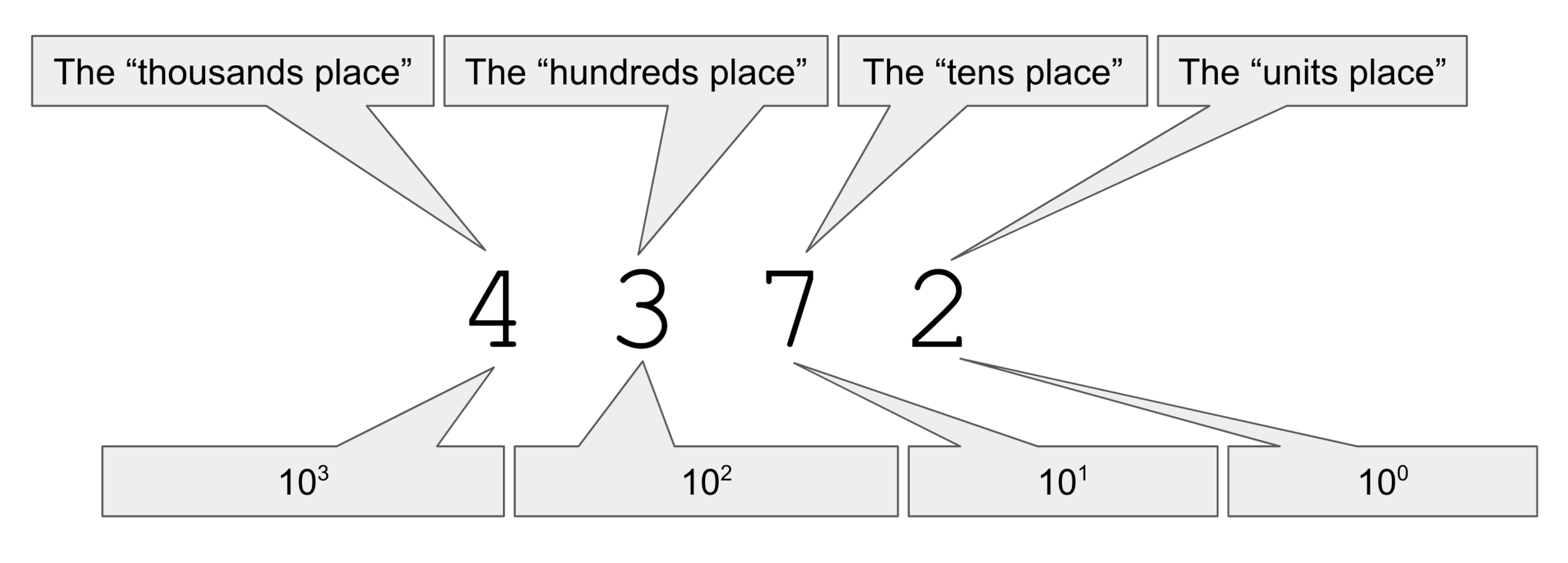
Positional Number Systems

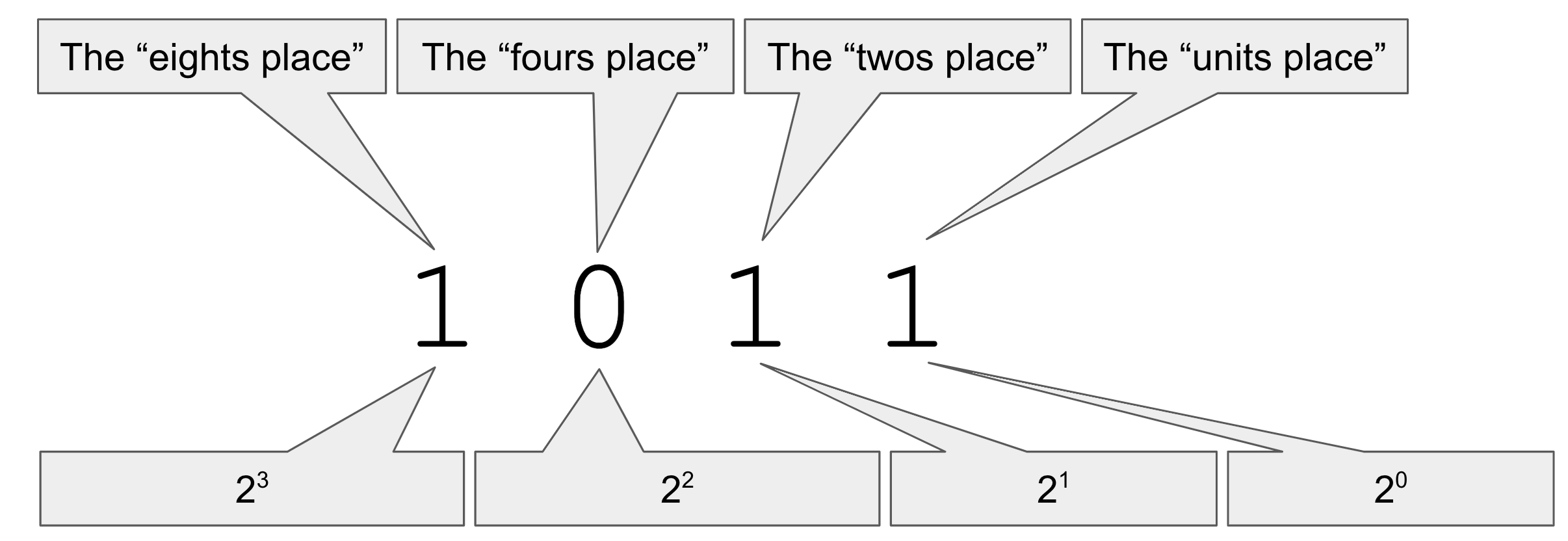
Positional Number Systems

STOP+THINK. Count to ten in binary

0000

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1x20

1x21+0

1x21+1x20

1x22+0+0

1x22+0+1x20

1x22+1x21+0

1x22+1x21+1x20

1x23+0+0+0

1x23+0+0+1x20

1x23+0+1x21+0

0

1

2

3

4

5

6

7

8

9

10

How to convert dec to bin?

Start with decimal number, "D"

Divide by 2. 
Note the result.
Write down the remainder.

Repeat process with the result.

Continue until nothing left.

D=6

610 = 

Example: What is 610 in binary?

divide by 2

result = 3, remainder = 0

divide by 2

result = 1, remainder = 1

divide by 2

result = 0, remainder = 1

1 

1 

0 

2 

DEC2BIN Algorithm

Start with decimal number, "D"

Divide by 2. 
Note the result.
Write down the remainder.

Repeat process with the result.

Continue until nothing left.

call decimal number D

divide D by 2

write remainder R to L

replace D with result

result=0?

read remainders

STOP+THINK. Convert 123 to binary

123 / 2 Q=61, R=1

1

 61 / 2 Q=30, R=1

30 / 2 Q=15, R=0

15 / 2 Q=7, R=1

7 / 2 Q=3, R=1

3 / 2 Q=1, R=1

1 / 2 Q=0, R=1

1

1

0

1

1

1

64

32

+

16

+

8

+

0

+

2

+

1

+

STOP+THINK. Convert 273 to binary

left as an exercise

See Also: "How to convert 273 to binary"

STOP+THINK. Convert 2421 to binary

left as an exercise

left as an exercise

STOP+THINK. Convert 77777 to binary

left as an exercise

STOP+THINK. The rest of binary 0 - 15 

0000   0100   1000   1100
0001   0101   1001   1101
0010   0110   1010   1110
0011   0111   1011   1111

 

1011

1100

1111

1110

1101

11

12

13

14

15

Other Bases

What if...

1

2

3

4

5

6

0, 1, 2, 3, 4, 5, ?

STOP+THINK. What's next?

Base 6

  64    63    62    61    60
1296  216    36     6     1
3*36 + 2*6 + 4*1

,10

,15

,14

,13

,12

,11

,20

3246 =

     =     12410

     =   108  + 12  + 4

Example

The powers of 6

0, 1, 2, 3, 4, 5, 10, 11, 12, 13, 14, 15, 20

STOP+THINK. What's next?

Back

More...

Base 6

Back

  64    63    62    61    60
1296  216    36     6     1
3246 =               3*36 + 2*6 + 4*1          
     =               108  + 12  + 1
     =               12110

What if...

0,1,2,3,4,5,6,7,8,9,10,11,12

By analogy...

,13

,14

,15

,10

,11...

we need some new symbols

,D

,E

,F

,A

,B

,C

Introducing: HEXADECIMAL NUMBERS

Three Number Systems

Binary Digits: 0,1

Hexadecimal Digits: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F

Decimal Digits: 0,1,2,3,4,5,6,7,8,9

Positions: 

1 s

1 000s

1 00s

1 0s

1 s

8s

4s

2s

Positions: 

1 s

4096s

256s

16s

Positions: 

BIN & HEX have a special relationship

4 binary digits can represent 16 values

hexadecimal has 16 symbols

Each hexadecimal digit has a 4 bit equivalent

1011

1100

1111

1110

1101

B

C

D

E

F

1010

1001

1000

0111

0110

0101

0100

0000

0001

0010

0011

A

0

1

2

4

3

5

9

7

6

8

BINARY & HEXADECIMAL have a special relationship

24     23     22     21     20
16     8      4      2      1
  164    163    162    161    160
65536   4096    256   16      1

BIN2HEX

1011010101010111101010111100

B

1011   0101   0101   0111   1010   1011   1100

{

A 

7

5

5

B

C 

GROUPS OF FOUR BITS

HEX EQUIVALENT

HEX2BIN

1011010101010111101010111100

1011

B        5         5          7          A          B         C

{

1100

1011

1010

0111

0101

0101

HEX2DEC

3 x 163     +  10 x 162  +  15 x 161  + 7 x 160

3 x 4096   +  10 x 256  +  15 x 16   +   7 x 1

12288    +     2560     +      240      +      7 

15095   

3

A

F

7

STOP+THINK. HEX2DEC 

FF
111
200
ACE
C0DE
1000
=15*16+15=25510
=256+16+1=27310
=2*256=51210
=10*256+12*16+14
=2560+206=276610
=12*4096+13*16+14
=49152+0+208+14
=4937410
=409610
162=256   163=4096

Click for solutions

ENCODING

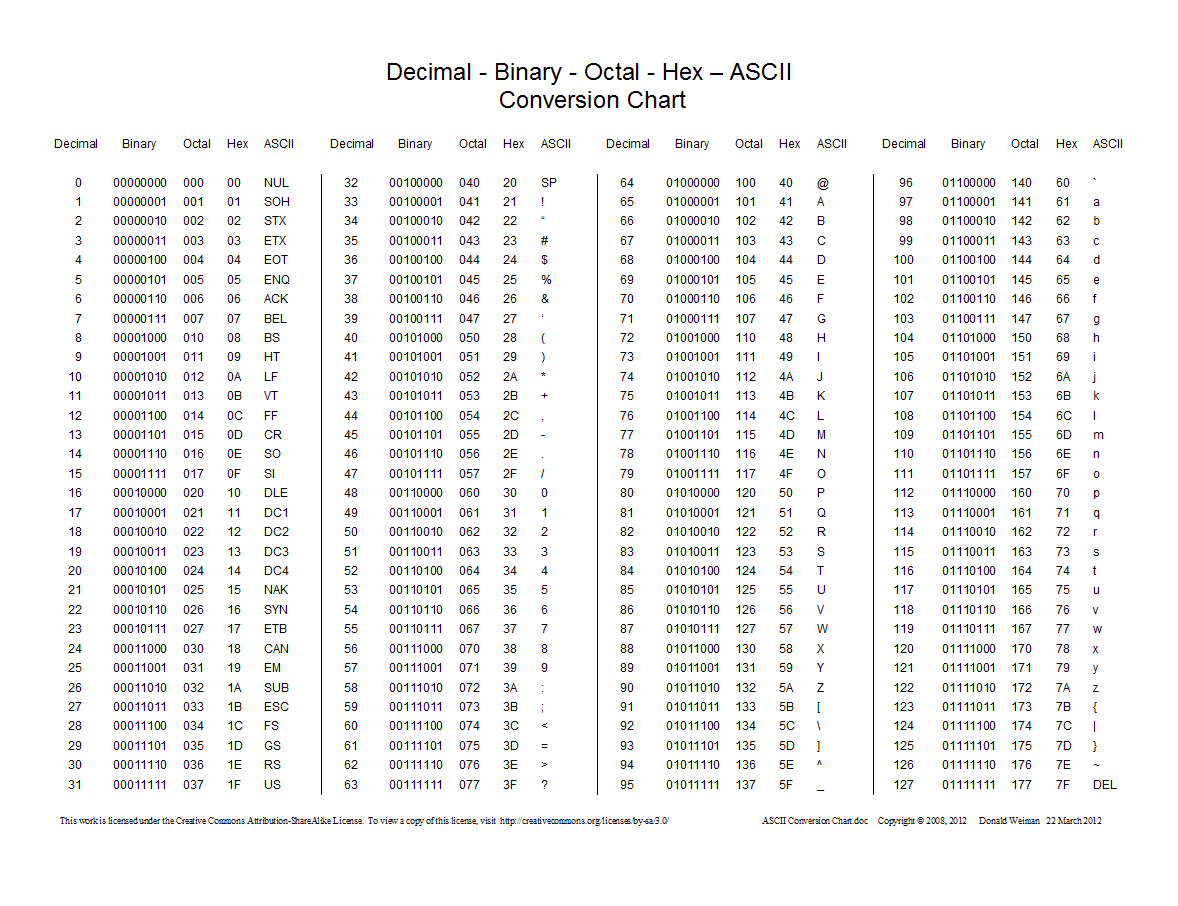
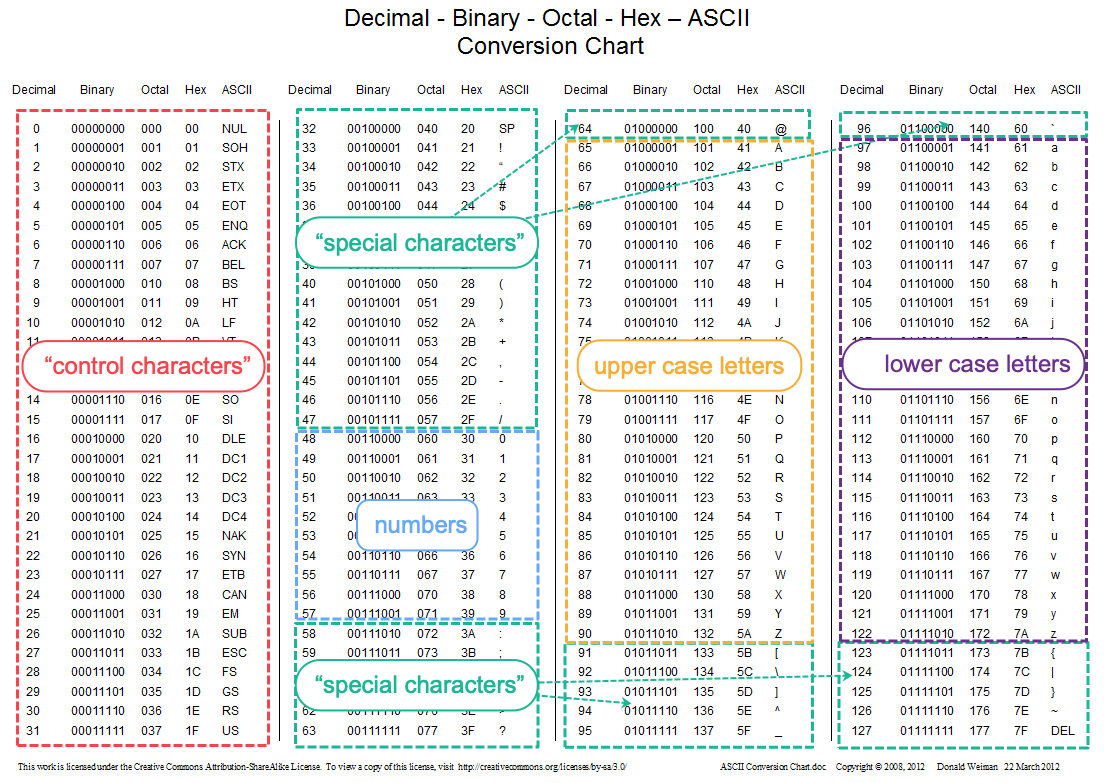
ASCII

American Standard Code for Information Interchange

  • Numerical code for letters, digits, symbols
     
  • Goes back to the days of teletype, hence the
    control character symbols such as BEL
     
  • Seven binary digits encode 128 symbols

STOP+THINK. Decode this ASCII text 

4465636F 64652074
68697320 41534349
49207465 787460

D

e

c

o

d

e

<sp>

t

h

i

s

C

A

S

<sp>

I

I

.

t

e

x

t

<sp>

STOP+THINK. Decode this ASCII text

Decode this ASCII text.

74=t 65=e 78=x 74=t 60=.

44=D  65=e 63=c 6F=o 64=d 65=e 20=SP
74=t 68=h 69=i 73=s 20=SP
41=A 53=S 43=C 49=I 49=I 20=SP

Other Notations

subscripts: 15916    159hex    159h

prefix: 0x1F9

special characters in URLs as hex pairs prefixed with %

characters in XML and HTML as hex pairs with &#xcode;

colors in HTML & CSS: 3 hex pairs* (red, green and blue) prefixed with #

http://www.example.com/name%20with%20spaces
&#x2019; = character U+2019 (’).

This Orange = #FFAA33

*CSS allows 3-hex digit abbreviation, one per component: #FA3 = #FFAA33.

COLORS in HTML

colors in HTML & CSS: 3 hex pairs* (red, green and blue) prefixed with #

This Orange = #FFAA33

*CSS allows 3-hex digit abbreviation, one per component: #FA3 = #FFAA33.

255/255 RED

51/255 BLUE

255/255 GREEN

STOP+THINK: CSS Colors

#17e71e

#abcdef

#8800FF

Which color is

#17e71e

#abcdef

#8800FF

See also: "HTML Symbols"

STOP+THINK: HTML &codes

Text

N.B.  16110 = 0xA1

Wait, there's more...

Part 2: Practice

How to Do Negative Numbers in Binary?

One's Complement

Represent number in N bits, e.g., 10210=0110 01102
Invert each bit: 1001 1001

DEC     BIN        1's Comp     DEC
  0  0000 0000 >> 1111 1111      -0
  1  0000 0001 >> 1111 1110      -1
  2  0000 0010 >> 1111 1101      -2
..
126  0111 1110 >> 1000 0001    -126
127  0111 1111 >> 1000 0000    -127

Sum of X and -X is 2N-1

"Two's Complement"

How many bits?

Write the positive binary value for the negative number.
Invert each bit in the number.
Add 1.

0101


Find two's complement for -25 in 8 bits
Find two's complement for -25 in 4 bits
Can't be done because 4 bit two's complement goes from 1000 (-8) to 1111 (-1)
0001 1001
Find two's complement for -5 in 4 bits

0101
1010


0101
1010
  +1


0101
1010
  +1
1011
0001 1001
1110 0110
0001 1001
1110 0110
       +1
0001 1001
1110 0110
       +1
1110 0111

"Two's Complement"

-17
001 0001
0001 0001
0111 1110
+1
0111 1111

This is a One Pixel PNG File

0000000 89 50 4e 47 0d 0a 1a 0a 00 00 00 0d 49 48 44 52
0000010 00 00 00 02 00 00 00 02 08 06 00 00 00 72 b6 0d
0000020 24 00 00 00 01 73 52 47 42 00 ae ce 1c e9 00 00
0000030 00 78 65 58 49 66 4d 4d 00 2a 00 00 00 08 00 04
0000040 01 1a 00 05 00 00 00 01 00 00 00 3e 01 1b 00 05
0000050 00 00 00 01 00 00 00 46 01 28 00 03 00 00 00 01
0000060 00 02 00 00 87 69 00 04 00 00 00 01 00 00 00 4e
0000070 00 00 00 00 00 00 00 90 00 00 00 01 00 00 00 90
0000080 00 00 00 01 00 03 a0 01 00 03 00 00 00 01 00 01
0000090 00 00 a0 02 00 04 00 00 00 01 00 00 00 02 a0 03
00000a0 00 04 00 00 00 01 00 00 00 02 00 00 00 00 3f 95
00000b0 04 0b 00 00 00 09 70 48 59 73 00 00 16 25 00 00
00000c0 16 25 01 49 52 24 f0 00 00 00 0b 49 44 41 54 08
00000d0 1d 63 60 40 07 00 00 12 00 01 80 14 ca cc 00 00
00000e0 00 00 49 45 4e 44 ae 42 60 82                  
00000ea

Resources

https://www.csfieldguide.org.nz/en/interactives/pixel-viewer/

BINARY ARITHMETIC

  • ADDING SINGLE BITS TOGETHER
  • THE CARRY BIT
  • MULTIPLYING IN BINARY

Binary
Arithmetic

 1
+1
10

Arithmetic in Binary

0 + 0 = 0

0 + 1 = 1

1 + 1 = 10

10 + 1 = 11

10 + 10 = 100

STOP+THINK
Could we write
numbers
with TimBits?

STOP+THINK
Could we do math
with TimBits? 

 1
+0
01

 0
+1
01

 0
+0
00

 1
+1
10

  A
 +B
 WX

A B  W X 
1 1  1 0
1 0  0 1
0 1  0 1
0 0  0 0

1. Fill in the missing figures

2. Multiply

111
x101

1010
x1010

3. Add

1111
1011
+10011

4. Compute the 3 bit 2's complement of the numbers -8 to -1

-8
1000
0111
0111
  +1
1000
-7
0111
1000
1000
  +1
1001
-6
0110
1001
1001
  +1
1010
-5
0101
1010
1010
  +1
1011
-4
0100
1011
1011
  +1
1100
-3
1100
1100
  +1
1101
-2
1101
1101
+1
1110
-1
1110
1110
  +1
1111
0001
0010
0011

5. Use 2's complement to compute

0101
+1101
1 0010
0011
+1011
1110
0110
+1010
0000
1011
+1101
1000

6.  Write -127 and -128 as 8-bit 2's complement numbers.  Examine the 7 right-most bits separately from the left-most or "most significant" bit.  If you treat these as an ordinary binary number, what value does a 1 in the most significant bit position seem to have in 2s complement notation?

7.  Write -32 and -31 as 6-bit 2's complement numbers.  Examine the 5 right-most bits separately from the left-most or "most significant" bit.  If you treat these as an ordinary binary number, what value does a 1 in the most significant bit position seem to have in 2s complement notation?

8.  Make an addition table for 3 bit binary numbers.

000 001 010 011 100 101 110 111
000
001
010
011 0110
100 1000
101 1010 1011 1100
110 1100 1101
111 1101 1110

9.  Suppose you had a black box that could add two or three bits together and produce two results, a sum bit and a carry bit.  Can you figure out how you might arrange a set of such black boxes to add two 2-bit binary numbers?

A

B

C

D

W

X

Y

AB
+CD
XYZ

10.  Make a multiplication table for 2 bit binary numbers.

AB
+CD
WXYZ
00 01 10 11
00
01
10
11

11.  Put the multiplication results into this table

AB
xCD
WXYZ
A B C D W X Y Z
0 0 0 0 0 0 0 0

Steganography (sort of)

Next: LOGIC