Labor Economics
Christopher Makler
Stanford University Department of Economics
Econ 50 | Lecture 21
Today's Agenda
- Labor Supply
- Labor Demand
- Is this model "true"?
Labor Supply
Leisure-Consumption Tradeoff
Leisure (R)
Consumption (C)
You trade \(L\) hours of labor for some amount of consumption, \(\Delta C\).
You start with 24 hours of leisure and \(M\) dollars.
You end up consuming \(R = 24 - L\) hours of leisure,
and \(C = M + \Delta C\) dollars worth of consumption.
Selling Labor at a Constant Wage
Leisure (R)
Consumption (C)
You sell \(L\) hours of labor at wage rate \(w\).
You start with 24 hours of leisure and \(M\) dollars.
You earn \(\Delta C = wL\) dollars in addition to the \(M\) you had.
...and you consume \(R = 24 - L\) hours of leisure.
Budget Line Equation
Leisure (R)
Consumption (C)
How does this compare to a normal budget line?
Optimal Supply of Labor
Preferences are over the two "good" things: leisure and consumption
We've just derived the budget constraint in terms of leisure and consumption as well:
Maximize utility as usual, with one caveat:
you can only sell your leisure time, not buy it.
pollev.com/chrismakler

Suppose \(u(R,C) = RC\), and your endowment is (24 hours, $1200 of nonwage income).
Sketch your budget line and indifference curve if \(w = 20\).
How much labor should you supply?
Hint: the key lies in figuring out the MRS at the endowment point...
Suppose \(u(R,C) = RC\), and your endowment is (24 hours, $1200 of nonwage income).
Sketch your budget line and indifference curve if \(w = 20\).
How much labor should you supply?
Hint: the key lies in figuring out the MRS at the endowment point...
Leisure (R)
Consumption
(C)
When will labor supply be zero?
Remember: you only want to sell good 1 (in this case, your time) if
Labor Demand
Remember our basic production function from our module on profit maximization:
Key insight for today: the profit-maximizing choice of \(q\) is also a profit-maximizing choice of \(L\).
The production function tells us the relationship between labor and output:
Profit is total revenues minus total costs:
e.g.
We can write this profit in terms of either choice variable:
CONDITIONAL DEMAND FOR LABOR
Profit as a function of quantity
Profit as a function of labor
1. Costs and Revenues
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
1. Costs and revenues
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
Profit two ways when \(p = 12\), \(w = 8\), \(r = 2\), and \(\overline K = 32\)
PROFIT-MAXIMIZING OUTPUT CHOICE
PROFIT-MAXIMIZING INPUT CHOICE
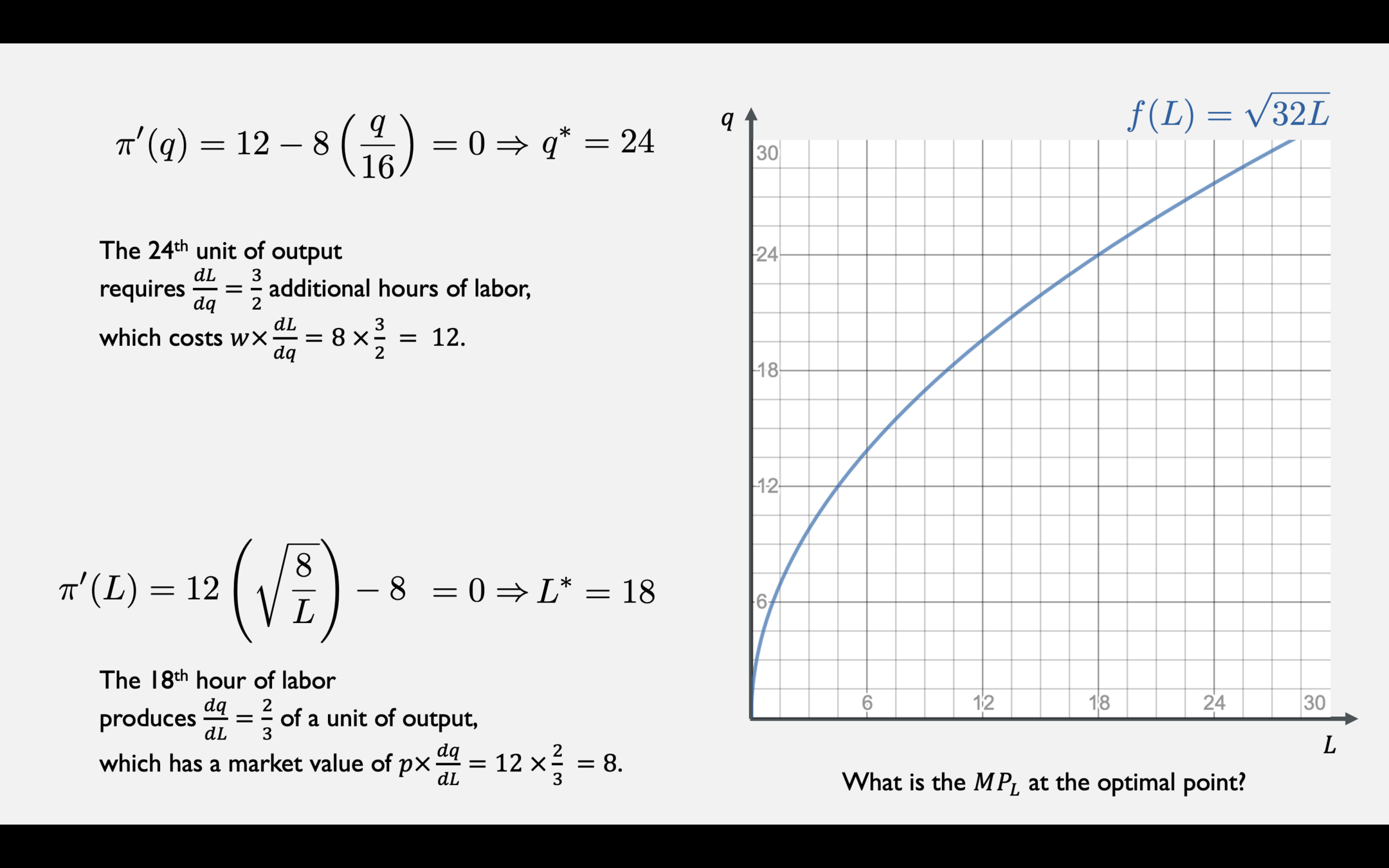
Profit as a function of output \(q\)
Profit as a function of labor \(L\)
1. Costs and revenue of the firm's choice
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
PROFIT-MAXIMIZING OUTPUT SUPPLY
PROFIT-MAXIMIZING LABOR DEMAND
PROFIT-MAXIMIZING
LABOR DEMAND FUNCTION
SUPPLY FUNCTION
the conditional labor demand
for the profit-maximizing supply:
The profit-maximizing labor demand is
CONDITIONAL LABOR DEMAND FUNCTION
Profit as a function of output \(q\)
Profit as a function of labor \(L\)
1. Costs for general \(w\) and revenue for general \(p\)
2. Profit = total revenues minus total costs
3. Take derivative of profit function, set =0
[cost of labor required for \(q\) units of output]
[revenue of output produced by \(L\) hours of labor]
MARGINAL COST (MC)
MARGINAL REVENUE PRODUCT OF LABOR (MRPL)
"Keep producing output as long as the marginal revenue from the last unit produced is at least as great as the marginal cost of producing it."
"Keep hiring workers as long as the marginal revenue from the output of the last worker is at least as great as the cost of hiring them."
Profit as a function of output \(q\)
Profit as a function of labor \(L\)
Is it true?
Are people paid the value of their marginal product?

What determines the value of people's work?
What should?
What determines how much people are paid?